Decoding of Convolutional Codes

1. Channel Coding
2. Faltungscodierung und geeignete Decoder
3. Decoding of Convolutional Codes

• Previous page
• Next page

• Previous page
• Next page

Blockschaltbild und Voraussetzungen

Ein wesentlicher Vorteil der Faltungscodierung ist, dass es hierfür mit dem Viterbi–Algorithmus ein sehr effizientes Decodierverfahren gibt. Dieser von Andrew James Viterbi entwickelte Algorithmus wurde bereits im Kapitel Viterbi–Empfänger des Buches „Digitalsignalübertragung” im Hinblick auf seinen Einsatz zur Entzerrung im Detail beschrieben.

Systemmodell zur Beschreibung der Decodierung von Faltungscodes

Für seinen Einsatz als Faltungsdecodierer gehen wir von folgendem Blockschaltbild und den folgenden Voraussetzungen aus:

• Die Informationssequenz $\underline{u} = (u_1, \ u_2, \ \text{...} \ )$ ist hier im Gegensatz zur Beschreibung der linearen Blockcodes   ⇒   Hauptkapitel 1 oder von Reed–Solomon–Codes   ⇒   Hauptkapitel 2 im allgemeinen unendlich lang („semi–infinite”). Für die Informationssymbole gilt stets $u_i ∈ \{0, 1\}$.
  

• Die Codesequenz $\underline{x} = (x_1, \ x_2, \ \text{...})$ mit $x_i ∈ \{0, 1\}$ hängt außer von $\underline{u}$ auch noch von der Coderate $R = 1/n$, dem Gedächtnis $m$ und der Übertragungsfunktionsmatrix $\mathbf{G}(D)$ ab. Bei endlicher Anzahl $L$ an Informationsbits sollte der Faltungscode durch Anfügen von $m$ Nullen terminiert werden:

\[\underline{u}= (u_1,\hspace{0.05cm} u_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, u_L, \hspace{0.05cm} 0 \hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.1cm}, 0 ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (x_1,\hspace{0.05cm} x_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, x_{2L}, \hspace{0.05cm} x_{2L+1} ,\hspace{0.05cm} \text{...} \hspace{0.1cm}, \hspace{0.05cm} x_{2L+2m} ) \hspace{0.05cm}.\]

• Die Empfangssequenz $\underline{y} = (y_1, \ y_2, \ \text{...} )$ ergibt sich entsprechend dem angenommenen Kanalmodell. Bei einem digitalen Modell wie dem Binary Symmetric Channel (BSC) gilt $y_i ∈ \{0, 1\}$, so dass die Verfälschung von $\underline{x}$ auf $\underline{y}$ mit der Hamming–Distanz $d_{\rm H}(\underline{x}, \underline{y})$ quantifiziert werden kann. Die erforderlichen Modifikationen für den AWGN–Kanal folgen im Abschnitt Viterbi–Algorithmus, basierend auf Korrelation und Metriken.

• Der nachfolgend beschriebene Viterbi–Algorithmus liefert eine Schätzung $\underline{z}$ für die Codesequenz $\underline{x}$ und eine weitere Schätzung $\underline{\upsilon}$ für die Informationssequenz $\underline{u}$. Dabei gilt:

\[{\rm Pr}(\underline{z} \ne \underline{x})\stackrel{!}{=}{\rm Minimum} \hspace{0.25cm}\Rightarrow \hspace{0.25cm} {\rm Pr}(\underline{\upsilon} \ne \underline{u})\stackrel{!}{=}{\rm Minimum} \hspace{0.05cm}.\]

$\text{Fazit:}$  Der Viterbi–Algorithmus sucht bei einem digitalen Kanalmodell (zum Beispiel BSC) von allen möglichen Codesequenzen $\underline{x}'$ diejenige Sequenz $\underline{z}$ mit der minimalen Hamming–Distanz $d_{\rm H}(\underline{x}', \underline{y})$ zur Empfangssequenz $\underline{y}$:

\[\underline{z} = {\rm arg} \min_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}( \underline{x}'\hspace{0.02cm},\hspace{0.02cm} \underline{y} ) = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm} \vert \hspace{0.05cm} \underline{x}')\hspace{0.05cm}.\]

Das bedeutet auch: Der Viterbi–Algorithmus erfüllt das Maximum–Likelihood–Kriterium.

Vorbemerkungen zu den nachfolgenden Decodierbeispielen (1)

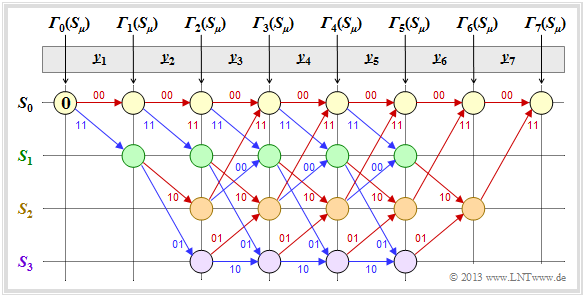
In den Beispielen dieses Kapitels wird stets von unserem Standard–Faltungscodierer der Rate $R = 1/2$, mit dem Gedächtnis $m = 2$ sowie der Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$ ausgegangen. Die Länge der Informationssequenz sei $L = 5$ und unter Berücksichtigung der Terminierung $L' = 7$. Die betrachteten Codesequenzen $\underline{x}$ und auch die Empfangssequenzen $\underline{y}$ setzen sich somit jeweils aus $14 \ \rm Bit$ zusammen. Durch Aufteilung entsprechend $\underline{y} = (\underline{y}_1, \ \underline{y}_2, \ ... \ , \ \underline{y}_7)$ ergeben sich die Bitpaare $\underline{y}_i ∈ \{00, 01, 10, 11\}$.

Trellis zur Decodierung der Empfangssequenz $\underline{y}$

Die Viterbi–Decodierung erfolgt mit Hilfe des dargestellten Trellisdiagramms. Ein roter Pfeil steht für die Hypothese $u_i = 0$, ein blauer für $u_i = 1$. Um Verwechslungen zu vermeiden, versehen wir hypothetische Größen mit Apostroph. Auch dann, wenn wir sicher wissen, dass das Informationsbit $u_i = 1$ ist, gilt $u_i' ∈ \{0, 1\}$. Neben den Pfeilen steht die jeweilige hypothetische Codesequenz $\underline{x}_i' ∈ \{00, 01, 10, 11\}$.

Wir gehen auf dieser und den nachfolgenden Seiten davon aus, dass die Viterbi–Decodierung auf der Hamming–Distanz $d_{\rm H}(\underline{x}_i', \ \underline{y}_i)$ zwischen dem Empfangswort $\underline{y}_i$ und den vier möglichen Codeworten $x_i' ∈ \{00, 01, 10, 11\}$ basiert. Dann gehen wir wie folgt vor:

• In den noch leeren Kreisen werden die Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ der Zustände $S_{\mu} (0 ≤ \mu ≤ 3)$ zu den Zeitpunkten $i$ eingetragen. Der Startwert ist stets ${\it \Gamma}_0(S_0) = 0$.

• Die Fehlergrößen für $i = 1$ und $i = 2$ ergeben sich zu

\[{\it \Gamma}_1(S_0) \hspace{-0.15cm} = \hspace{-0.15cm} d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm}, \hspace{2.13cm}{\it \Gamma}_1(S_1) = d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm},\]

\[{\it \Gamma}_2(S_0) \hspace{-0.15cm} = \hspace{-0.15cm}{\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.4cm}{\it \Gamma}_2(S_1) = {\it \Gamma}_1(S_0)+ d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm},\]

\[{\it \Gamma}_2(S_2) \hspace{-0.15cm} = \hspace{-0.15cm}{\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.4cm}{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1)+ d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm}.\]

Die Beschreibung wird auf der nächsten Seite fortgesetzt.

Vorbemerkungen zu den nachfolgenden Decodierbeispielen (2)

Fortsetzung der allgemeinen Viterbi–Beschreibung:

Trellis zur Decodierung der Empfangssequenz $\underline{y}$

• Ab dem Zeitpunkt $i = 3$ hat das Trellisdiagramm seine Grundform erreicht, und zur Berechnung aller ${\it \Gamma}_i(S_{\mu})$ muss jeweils das Minimum zwischen zwei Summen ermittelt werden:

\[{\it \Gamma}_i(S_0) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]

\[{\it \Gamma}_i(S_1) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]

\[{\it \Gamma}_i(S_2) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]

\[{\it \Gamma}_i(S_3) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm}.\]

• Von den zwei an einem Knoten ${\it \Gamma}_i(S_{\mu})$ ankommenden Zweigen wird der schlechtere (der zu einem größeren ${\it \Gamma}_i(S_{\mu})$ geführt hätte) eliminiert. Zu jedem Knoten führt dann nur noch ein einziger Zweig.
  

• Sind alle Fehlergrößen bis einschließlich $i = 7$ ermittelt, so kann der Viterbi–Algotithmus mit der Suche das zusammenhängenden Pfades vom Ende des Trellis ⇒ ${\it \Gamma}_7(S_0)$ bis zum Anfang ⇒ ${\it \Gamma}_0(S_0)$ abgeschlossen werden.
  

• Durch diesen Pfad liegen dann die am wahrscheinlichsten erscheinende Codesequenz $\underline{z}$ und die wahrscheinlichste Informationssequenz $\underline{\upsilon}$ fest. Nicht für alle Empfangssequenzen $\underline{y}$ gilt aber $\underline{z} = \underline{x}$ und $\underline{\upsilon} = \underline{u}$. Das heißt: Bei zu vielen Übertragungsfehlern versagt auch der Viterbi–Algorithmus.
  

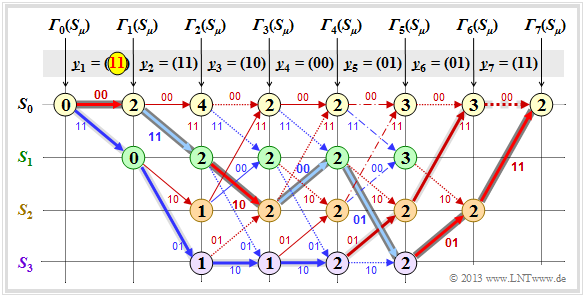
Decodierbeispiel für den fehlerfreien Fall (1)

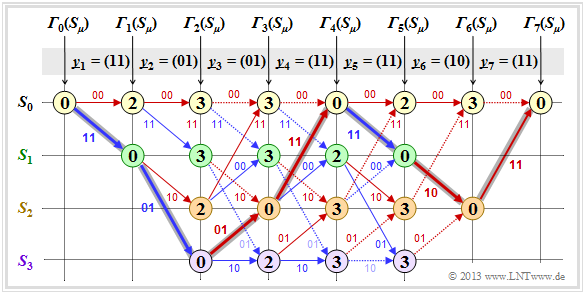
Zunächst gehen wir von der Empfangssequenz $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ aus, die hier – wegen der Codewortlänge $n = 2$ – bereits in Bitpaare $\underline{y}_1, \ ... \ , \ \underline{y}_7$ unterteilt ist.

Viterbi–Schema für $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$

Die eingetragenen Zahlenwerte und die verschiedenen Stricharten werden im folgenden Text erklärt:

• Ausgehend vom Initialwert ${\it \Gamma}_0(S_0) = 0$ kommt man mit $\underline{y}_1 = (11)$ durch Addition der Hamming-Distanzen $d_{\rm H}((00), \ \underline{y}_1) = 2$ bzw. $d_{\rm H}((11), \ \underline{y}_1) = 0$ zu den Fehlergrößen ${\it \Gamma}_1(S_0) = 2, \ {\it \Gamma}_1(S_1) = 0$.
  

• Im zweiten Decodierschritt gibt es Fehlergrößen für alle vier Zustände: Mit $\underline{y}_2 = (01)$ erhält man:

\[{\it \Gamma}_2(S_0) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]

\[{\it \Gamma}_2(S_1) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Gamma}_1(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]

\[{\it \Gamma}_2(S_2) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+2=2 \hspace{0.05cm},\]

\[{\it \Gamma}_2(S_3) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Gamma}_1(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+0=0 \hspace{0.05cm}.\]

• In allen weiteren Decodierschritten müssen jeweils zwei Werte verglichen werden, wobei dem Knoten ${\it \Gamma}_i(S_{\mu})$ stets der kleinere Wert zugewiesen wird. Beispielsweise gilt für $i = 3$ mit $\underline{y}_3 = (01)$:

\[{\it \Gamma}_3(S_0) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{2}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =\]

\[ \hspace{1.2cm} = \hspace{-0.15cm}{\rm min} \left [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \right ] = 3\hspace{0.05cm},\]

\[{\it \Gamma}_3(S_3) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{2}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =\]

\[ \hspace{1.2cm} = \hspace{-0.15cm}{\rm min} \left [ 3+0\hspace{0.05cm},\hspace{0.05cm} 0+2 \right ] = 2\hspace{0.05cm}.\]

• Ab $i = 6$ wird im betrachteten Beispiel die Terminierung des Faltungscodes wirksam. Hier sind nur noch zwei Vergleiche zur Bestimmung von ${\it \Gamma}_6(S_0)$ und ${\it \Gamma}_6(S_2)$ anzustellen, und für $i = 7$ nur noch ein Vergleich mit dem Endergebnis ${\it \Gamma}_7(S_0)$.
  

• Von den jeweils zwei an einem Knoten ankommenden Zweigen wird stets nur derjenige bei der abschließenden Pfadsuche herangezogen, der zur minimalen Fehlergröße ${\it \Gamma}_i(S_{\mu})$ geführt hat. Die „schlechten” Zweige werden verworfen. Sie sind in obiger Grafik jeweils punktiert dargestellt.
  
  

Die Beschreibung wird auf der nächsten Seite fortgesetzt.

Decodierbeispiel für den fehlerfreien Fall (2)

Nachdem alle Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – in dem vorliegenden Beispiel für $1 ≤ i ≤ 7$ und $0 ≤ \mu ≤ 3$ – ermittelt wurden, kann der Viterbi–Decoder mit der Pfadsuche beginnen.

Viterbi–Pfadsuche für $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$

Die Pfadsuche läuft wie folgt ab:

• Ausgehend vom Endwert ${\it \Gamma}_7(S_0)$ wird in Rückwärtsrichtung ein zusammenhängender Pfad bis zum Startwert ${\it \Gamma}_0(S_0)$ gesucht. Erlaubt sind nur die durchgezogenen Zweige. Punktierte Linien können nicht Teil des ausgewählten Pfades sein.
  

• Der ausgewählte Pfad ist in der Grafik grau markiert. Er durchläuft von rechts nach links die Zustände $S_0 ← S_2 ← S_1 ← S_0 ← S_2 ← S_3 ← S_1 ← S_0$. Es gibt keinen zweiten durchgehenden Pfad von ${\it \Gamma}_7(S_0)$ zu ${\it \Gamma}_0(S_0)$. Das bedeutet: Das Decodierergebnis ist eindeutig.
  

• Das Ergebnis $\underline{\upsilon} = (1, 1, 0, 0, 1, 0, 0)$ des Viterbi–Decoders hinsichtlich der Informationssequenz erhält man, wenn man für den durchgehenden Pfad – nun aber in Vorwärtsrichtung von links nach rechts – die Farben der einzelnen Zweige auswertet (rot entspricht einer $0$, blau einer $1$).
  
  

Aus dem Endwert ${\it \Gamma}_7(S_0) = 0$ erkennt man, dass in diesem ersten Beispiel keine Übertragungsfehler vorlagen. Das Decodierergebnis $\underline{z}$ stimmt also mit dem Empfangsvektor $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ und der tatsächlichen Codesequenz $\underline{x}$ überein. Außerdem ist $\underline{\upsilon}$ nicht nur die nach dem ML–Kriterium wahrscheinlichste Informationssequenz $\underline{u}$, sondern es gilt auch hier die Identität: $\underline{\upsilon} = \underline{u}$.

Anmerkung: Bei der beschriebenen Decodierung wurde von der bereits in der Überschrift enthaltenen Information „Fehlerfreier Fall” natürlich kein Gebrauch gemacht wurde.

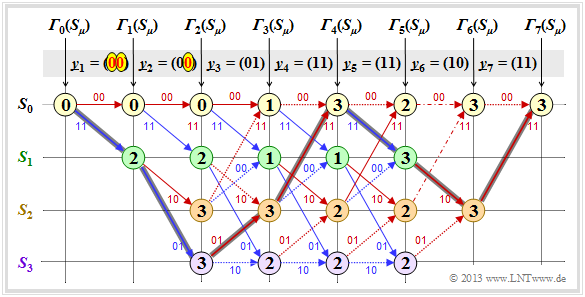
Decodierbeispiele für den fehlerbehafteten Fall (1)

Es folgen zwei weitere Beispiele zur Viterbi–Decodierung. Die Berechnung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ geschieht wie auf Seite 2 beschrieben und auf der letzten Seite für den fehlerfreien Fall demonstriert.

Decodierbeispiel mit zwei Bitfehlern

Als Resümee dieses ersten Beispiels mit obigem Trellis ist festzuhalten:

• Auch hier lässt sich ein eindeutiger Pfad (dunkelgraue Markierung) zurückverfolgen, der zu den folgenden Ergebnissen führt (erkennbar an den Beschriftungen bzw. den Farben dieses Pfades):

\[\underline{z} \hspace{-0.15cm} = \hspace{-0.15cm} \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \big ) \hspace{0.05cm},\]

\[ \underline{\upsilon} \hspace{-0.15cm} = \hspace{-0.15cm} \big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big ) \hspace{0.05cm}.\]

• Der Vergleich der am wahrscheinlichsten gesendeten Codesequenz $\underline{z}$ mit dem Empfangsvektor $\underline{y}$ zeigt, dass hier zwei Bitfehler (am Beginn) vorlagen. Da aber der verwendete Faltungscode die freie Distanz $d_{\rm H} = 5$ aufweist, führen zwei Fehler noch nicht zu einem falschen Decodierergebnis.
  

• Es gibt andere Pfade wie zum Beispiel den heller markierten Pfad $(S_0 → S_1 → S_3 → S_3 → S_3 → S_2 → S_0 → S_0)$, die zunächst als vielversprechend erscheinen. Erst im letzten Decodierschritt $(i = 7)$ kann dieser hellgraue Pfad endgültig verworfen werden.
  

• Dieses Beispiel zeigt, dass eine zu frühe Entscheidung oft zu einem Decodierfehler führt, und man erkennt auch die Zweckmäßigkeit der Terminierung: Bei endgültiger Entscheidung zum Zeitpunkt $i = 5$ (dem Ende der eigentlichen Informationssequenz) wären die Sequenzen $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 1, 0)$ noch als gleichwahrscheinlich angesehen worden.
  
  

Anmerkung: Bei der Berechnung von ${\it \Gamma}_5(S_0) = 3$ und ${\it \Gamma}_5(S_1) = 3$ führen hier jeweils die beiden Vergleichszweige zur gleichen minimalen Fehlergröße. In der Grafik sind diese beiden Sonderfälle durch Strichpunktierung markiert.

In diesem Beispiel hat dieser Sonderfall keine Auswirkung auf die Pfadsuche. Der Algorithmus erwartet trotzdem stets eine Entscheidung zwischen zwei konkurrierenden Zweigen. In der Praxis hilft man sich dadurch, dass man bei Gleichheit einen der beiden Pfade zufällig auswählt.

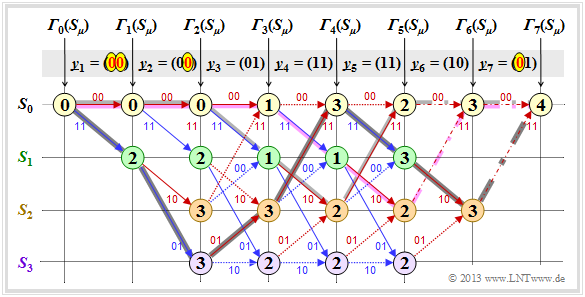
Decodierbeispiele für den fehlerbehafteten Fall (2)

Im letzten Beispiel gehen wir stets von folgenden Voraussetzungen bezüglich Quelle und Coder aus:

\[\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.\]

Aus der ersten der beiden Grafiken erkennt man, dass sich hier der Decoder trotz dreier Bitfehler für den richtigen Pfad (dunkle Hinterlegung) entscheidet. Es gibt also nicht immer eine Fehlentscheidung, wenn mehr als $d_{\rm F}/2$ Bitfehler aufgetreten sind.

Decodierbeispiel mit drei Bitfehlern

In der unteren Grafik ist noch ein vierter Bitfehler in Form von $\underline{y}_7 = (01)$ hinzugefügt:

• Nun führen beide Zweige im Schritt $i = 7$ zur minimalen Fehlergröße ${\it \Gamma}_7(S_0) = 4$, erkennbar an den strichpunktierten Übergängen. Entscheidet man sich im dann erforderlichen Losverfahren für den dunkel hinterlegten Pfad, so wird auch bei vier Bitfehlern noch die richtige Entscheidung getroffen.
  

• Andernfalls kommt es zu einer Fehlentscheidung. Je nachdem, wie das Auswürfeln im Schritt $i =6$ zwischen den beiden strichpunktierten Konkurrenten ausgeht, entscheidet man sich entweder für den violetten oder den hellgrauen Pfad. Mit dem richtigen Pfad haben beide wenig gemein.
  

Decodierbeispiel mit vier Bitfehlern

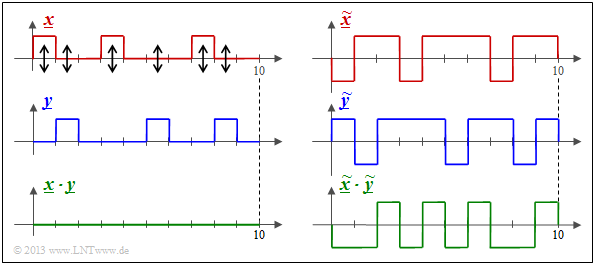
Zusammenhang zwischen Hamming–Distanz und Korrelation

Insbesondere beim BSC–Modell – aber auch bei jedem anderen Binärkanal  ⇒  Eingang $x_i ∈ \{0,1\}$, Ausgang $y_i ∈ \{0,1\}$ wie zum Beispiel dem Gilbert–Elliott–Modell – liefert die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{y})$ genau die gleiche Information über die Ähnlichkeit der Eingangsfolge $\underline{x}$ und der Ausgangsfolge $\underline{y}$ wie das innere Produkt. Nimmt man an, dass die beiden Folgen in bipolarer Darstellung vorliegen (gekennzeichnet durch Tilden) und dass die Folgenlänge jeweils $L$ ist, so gilt für das innere Produkt:

\[<\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} = \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.\]

Wir bezeichnen dieses innere Produkt manchmal auch als „Korrelationswert”. Die Anführungszeichen sollen darauf hinweisen, dass der Wertebereich eines Korrelationskoeffizienten eigentlich $±1$ ist.

: Wir betrachten hier zwei Binärfolgen der Länge $L = 10$:

Zusammenhang zwischen Haming–Distanz und „Korrelation”

• Links dargestellt sind die unipolaren Folgen $\underline{x}$ und $\underline{y}$ sowie das Produkt $\underline{x} \cdot \underline{y}$. Man erkennt die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{y}) = 6$  ⇒  sechs Bitfehler an den Pfeilpositionen. Das innere Produkt $〈\underline{x} \cdot \underline{y}〉 = 0$ hat hier keine Aussagekraft. Zum Beispiel ist $〈\underline{0} \cdot \underline{y}〉$ unabhängig von $\underline{y}$ stets Null.

• Die Hamming–Distanz $d_{\rm H} = 6$ erkennt man auch aus der bipolaren (antipodalen) Darstellung der rechten Grafik. Die „Korrelationswert” hat aber nun den richtigen Wert $4 \cdot (+1) + 6 \cdot (–1) = \, –2$. Es gilt der deterministische Zusammenhang zwischen den beiden Größen mit der Folgenlänge $L$:

\[<\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} = L - 2 \cdot d_{\rm H} (\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}})\hspace{0.05cm}.\]

Interpretieren wir nun diese Gleichung für einige Sonderfälle:

• Identische Folgen: Die Hamming–Distanz ist gleich $0$ und der „Korrelationswert” gleich $L$.
  

• Invertierte: Folgen: Die Hamming–Distanz ist gleich $L$ und der „Korrelationswert” gleich $–L$.
  

• Unkorrelierte Folgen: Die Hamming–Distanz ist gleich $L/2$, der „Korrelationswert” gleich $0$.
  
  

Viterbi–Algorithmus, basierend auf Korrelation und Metriken

Mit den Erkenntnissen der letzten Seite lässt sich der Viterbi–Algorithmus auch wie folgt charakterisieren. Der Algorithmus sucht von allen möglichen Codesequenzen $\underline{x}' ∈ C$ die Sequenz $\underline{z}$ mit der maximalen Korrelation zur Empfangssequenz $\underline{y}$:

\[\underline{z} = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} \left\langle \tilde{\underline{x}}'\hspace{0.05cm} ,\hspace{0.05cm} \tilde{\underline{y}} \right\rangle \hspace{0.4cm}{\rm mit }\hspace{0.4cm}\tilde{\underline{x}}'= 1 - 2 \cdot \underline{x}'\hspace{0.05cm}, \hspace{0.2cm} \tilde{\underline{y}}= 1 - 2 \cdot \underline{y} \hspace{0.05cm}.\]

$〈 ... 〉$ bezeichnet einen „Korrelationswert” entsprechend den Aussagen auf der letzten Seite. Die Tilden weisen wieder auf die bipolare (antipodale) Darstellung hin.

Die Grafik zeigt die diesbezügliche Trellisauswertung. Zugrunde liegt

• der gleiche Faltungscode mit $R = 1/2, m = 2$ und $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$, und
  

• der gleiche Empfangsvektor $\underline{y} = (11, 11, 10, 00, 01, 01, 11)$
  
  

wie für das Trellisdiagramm auf Seite 3a dieses Kapitels, basierend auf der minimalen Hamming–Distanz und den Fehlergrößen ${\it \Gamma}_i(S_{\mu})$. Beide Darstellungen ähneln sich sehr.

Viterbi–Decodierung, basierend auf Korrelation und Metrik

Ebenso wie die Suche nach der Sequenz mit der minimalen Hamming–Distanz geschieht auch die Suche nach dem maximalen Korrelationswert schrittweise:

• Die Knoten bezeichnet man hier als die Metriken ${\it \Lambda};_i(S_{\mu})$. Die englische Bezeichnung hierfür ist Cumulative Metric, während Branch Metric den Metrikzuwachs angibt.
  

• Der Endwert ${\it \Lambda};_7(S_0) = 10$ gibt den „Korrelationswert” zwischen der ausgewählten Folge $\underline{z}$ und dem Empfangsvektor $\underline{y}$ an. Im fehlerfreien Fall ergäbe sich ${\it \Lambda};_7(S_0) = 14$.
  
  

Die Trellisbeschreibung wird auf der nächsten Seite fortgesetzt.

Viterbi–Algorithmus, basierend auf Korrelation und Metriken (2)

Die nachfolgende Beschreibung bezieht sich auf die Trellisauswertung entsprechend der letzten Seite, basierend auf „Korrelationswerten” und den Metriken ${\it \Lambda}_i(S_{\mu})$. Zum Vergleich zeigt die Grafik auf Seite 3a Trellisauswertung, die auf Hamming–Distanzen und den Fehlergrößen $\Gamma_i(S_{\mu})$ basieren.

• Die Metriken zum Zeitpunkt $i = 1$ ergeben sich mit $\underline{y}_1 = (11)$ zu

\[{\it \Lambda}_1(S_0) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(+1,\hspace{0.05cm} +1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} -2 \hspace{0.05cm},\]

\[{\it \Lambda}_1(S_1) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(-1,\hspace{0.05cm} -1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} +2 \hspace{0.05cm}.\]

• Entsprechend gilt zum Zeitpunkt $i = 2$ mit $\underline{y}_2 = (11)$:

\[{\it \Lambda}_2(S_0) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2-2 = -4 \hspace{0.05cm},\]

\[{\it \Lambda}_2(S_1) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2+2 = 0 \hspace{0.05cm},\]

\[{\it \Lambda}_2(S_2) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} 2+0 = 2 \hspace{0.05cm},\]

\[{\it \Lambda}_2(S_3) \hspace{-0.15cm} = \hspace{-0.15cm} {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} 2+0 = 2 \hspace{0.05cm}.\]

• Ab dem Zeitpunkt $i =3$ muss eine Entscheidung zwischen zwei Metriken getroffen werden. Beispielsweise erhält man mit $\underline{y}_3 = (10)$ für die oberste und die unterste Metrik im Trellis:

\[{\it \Lambda}_3(S_0) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm max} \left [{\it \Lambda}_{2}(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}> \right ] =\]

\[\hspace{1.25cm} = \hspace{-0.15cm} {\rm max} \left [ -4+0\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] = 2\hspace{0.05cm},\]

\[{\it \Lambda}_3(S_3) \hspace{-0.15cm} = \hspace{-0.15cm}{\rm max} \left [{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_3) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}> \right ] =\]

\[\hspace{1.25cm} = \hspace{-0.15cm} {\rm max} \left [ 0+0\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] = 4\hspace{0.05cm}.\]

Vergleicht man die zu minimierenden Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ mit den zu maximierenden Metriken ${\it \Lambda}_i(S_{\mu})$, so erkennt man den folgenden deterministischen Zusammenhang:

\[{\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [ i - {\it \Gamma}_i(S_{\mu}) \big ] \hspace{0.05cm}.\]

Die Auswahl der zu den einzelnen Decodierschritten überlebenden Zweige ist bei beiden Verfahren identisch, und auch die Pfadsuche liefert das gleiche Ergebnis.

Zusammenfassung:

• Beim Binärkanal – zum Beispiel dem BSC–Modell – führen die beiden beschriebenen Viterbi–Varianten Fehlergrößenminimierung und Metrikmaximierung zum gleichen Ergebnis.
  

• Beim AWGN–Kanal ist die Fehlergrößenminimierung nicht anwendbar, da keine Hamming–Distanz zwischen dem binären Eingang $\underline{x}$ und dem analogen Ausgang $\underline{y}$ angegeben werden kann.
  

• Die Metrikmaximierung ist beim AWGN–Kanal vielmehr identisch mit der Minimierung der Euklidischen Distanz – siehe Aufgabe Z3.10.
  

• Ein weiterer Vorteil der Metrikmaximierung ist, dass eine Zuverlässigkeitsinformation über die Empfangswerte $\underline{y}$ in einfacher Weise berücksichtigt werden kann.
  

Viterbi–Entscheidung bei nicht–terminierten Faltungscodes (1)

Bisher wurde stets ein terminierter Faltungscode der Länge $L' = L + m$ betrachtet, und das Ergebnis des Viterbi–Decoders war der durchgehende Trellispfad vom Startzeitpunkt $(i = 0)$ bis zum Ende $(i = L')$.

Bei nicht–terminierten Faltungscodes $(L' → ∞)$ ist diese Entscheidungsstrategie nicht anwendbar. Hier muss der Algorithmus abgewandelt werden, um in endlicher Zeit eine bestmögliche Schätzung (gemäß Maximum–Likelihood) der einlaufenden Bits der Codesequenz liefern zu können.

Beispielhaftes Trellis und überlebende Pfade

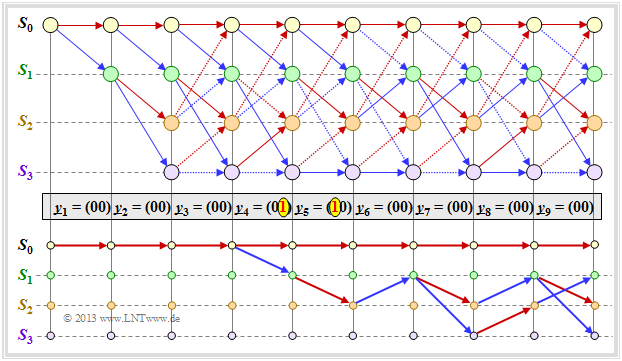
Die obere Grafik zeigt ein beispielhaftes Trellis für

• unseren Standard–Codierer   ⇒   $R = 1/2, \ m = 2, \ {\rm G}(D) = (1 + D + D^2, \ 1 + D^2)$,
  

• die Nullfolge ⇒ $\underline{u} = \underline{0} = (0, 0, 0, \ ...)$   ⇒   $\underline{x} = \underline{0} = (00, 00, 00, \ ...)$,
  

• jeweils einen Übertragungsfehler bei $i = 4$ und $i = 5$.
  
  

Anhand der Stricharten erkennt man erlaubte (durchgezogene) und verbotene (punktierte) Pfeile in rot $(u_i = 0)$ und blau $(u_i = 1)$. Punktierte Linien haben einen Vergleich gegen einen Konkurrenten verloren und können nicht Teil des ausgewählten Pfades sein.

Die untere Grafik zeigt die $2^m$ überlebenden Pfade ${\it \Phi}_i(S_{\mu})$ für den Zeitpunkt $i = 9$. Man findet diese Pfade am einfachsten von rechts nach links. Die folgende Angabe zeigt die durchlaufenen Zustände $S_{\mu}$ in Vorwärtsrichtung:

$${\it \Phi}_9(S_0) \text{:} \, S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0,$$

$${\it \Phi}_9(S_1) \text{:} \, S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_3 → S_2 → S_1,$$

$${\it \Phi}_9(S_2) \text{:} \, S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_2,$$

$${\it \Phi}_9(S_3) \text{:} \, S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_3.$$

Die Beschreibung wird auf der nächsten Seite fortgesetzt.

Viterbi–Entscheidung bei nicht–terminierten Faltungscodes (2)

: Der überlebende Pfad (englisch: Survivor) ${\it \Phi}_i(S_{\mu})$ ist der durchgehende Pfad vom Start $S_0$ (bei $i = 0$) zum Knoten $S_{\mu}$ zum Zeitpunkt $i$. Empfehlenswert ist die Pfadsuche in Rückwärtsrichtung.

Die überlebenden Pfade ${\it \Phi}_6, \ ... \ , \ {\it \Phi}_9$

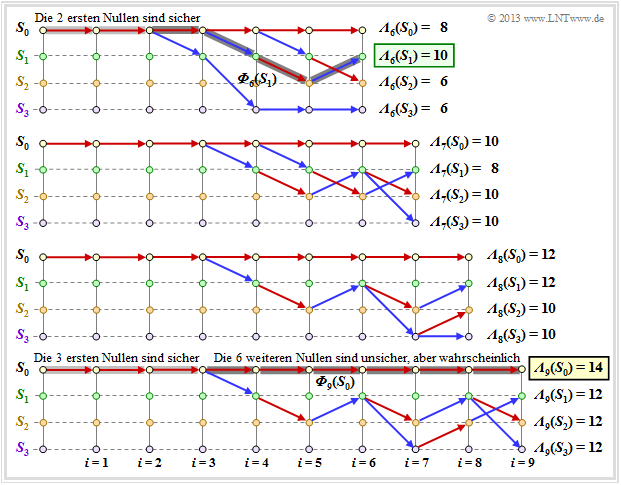
Die Grafik zeigt die überlebenden Pfade für die Zeitpunkte $i = 6$ bis $i = 9$. Zusätzlich sind die jeweiligen Metriken ${\it \Lambda}_i(S_{\mu})$ für alle vier Zustände angegeben. Die Grafik ist wie folgt zu interpretieren:

• Zum Zeitpunkt $i = 9$ kann noch keine endgültige ML–Entscheidung über die ersten neun Bit der Informationssequenz getroffen werden. Allerdings ist bereits sicher, dass die wahrscheinlichste Bitfolge durch einen der Pfade ${\it \Phi}_9(S_0), \ ... \ , \ {\it \Phi}_9(S_3)$ richtig wiedergegeben wird.
  

• Da alle vier Pfade bei $i = 3$ zusammenlaufen, ist die Entscheidung „$\upsilon_1 = 0, \ \upsilon_2 = 0, \ \upsilon_3 = 0$” die bestmögliche (hellgraue Hinterlegung). Auch zu einem späteren Zeitpunkt würde keine andere Entscheidung getroffen werden. Hinsichtlich der Bits $\upsilon_4, \ \upsilon_5, \ ...$ sollte man sich noch nicht festlegen.
  

• Müsste man zum Zeitpunkt $i = 9$ eine Zwangsentscheidung treffen, so würde man sich für ${\it \Phi}_9(S_0)$  ⇒  $\underline{\upsilon} = (0, 0, \ ... \ , 0)$ entscheiden, da die Metrik ${\it \Lambda}_9(S_0) = 14$ größer ist als die Vergleichsmetriken.
  

• Die Zwangsentscheidung zum Zeitpunkt $i = 9$ führt in diesem Beispiel zum richtigen Ergebnis. Zum Zeitpunkt $i = 6$ wäre ein solcher Zwangsentscheid falsch gewesen ⇒ $\underline{\upsilon} = (0, 0, 0, 1, 0, 1)$, und zu den Zeitpunten $i = 7$ bzw. $i = 8$ nicht eindeutig.
  

Weitere Decodierverfahren für Faltungscodes

Wir haben uns bisher in diesem Kapitel nur mit dem Viterbi–Algorithmus beschäftigt, der 1967 von A. J. Viterbi veröffentlicht wurde. Erst 1974 hat G. D. Forney nachgewiesen, dass dieser Algorithmus eine Maximum–Likelihood–Decodierung von Faltungscodes durchführt.

Aber schon in den Jahren zuvor waren viele Wissenschaftler sehr bemüht, effiziente Decodierverfahren für die 1955 erstmals von Peter Elias beschriebenen Faltungscodes bereitzustellen. Zu nennen sind hier unter Anderem – genauere Beschreibungen findet man beispielsweise in [Bos99].

• Sequential Decoding von J. M. Wozencraft und B. Reifen aus dem Jahre 1961,
  

• der Vorschlag von R. M. Fano (1963), der als Fano–Algorithmus bekannt wurde,
  

• die Arbeiten von K. Zigangirov (1966) und F. Jelinek (1969), deren Decodierverfahren häufig als Stack–Algorithmus bezeichnet wird.
  
  

Alle diese Decodierverfahren und auch der Viterbi–Algorithmus in seiner bisher beschriebenen Form liefern „hart” entschiedene Ausgangswerte ⇒ $\upsilon_i ∈ \{0, 1\}$. Oftmals wären jedoch Informationen über die Zuverlässigkeit der getroffenen Entscheidungen wünschenswert, insbesondere dann, wenn ein verkettetes Codierschema mit einem äußeren und einem inneren Code vorliegt.

Kennt man die Zuverlässigkeit der vom inneren Decoder entschiedenen Bits zumindest grob, so kann durch diese Information die Bitfehlerwahrscheinlichkeit des äußeren Decoders (signifikant) herabgesetzt werden. Der von J. Hagenauer in [Hag90] vorgeschlagene Soft–Output–Viterbi–Algorithmus (SOVA) erlaubt es, zusätzlich zu den entschiedenen Symbolen auch jeweils ein Zuverlässigkeitsmaß anzugeben.

Abschließend gehen wir noch etwas genauer auf den BCJR–Algorithmus ein, benannt nach dessen Erfinder L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv [BCJR74]. Während der Viterbi–Algorithmus nur eine Schätzung der Gesamtsequenz vornimmt  ⇒  block–wise ML, schätzt der BCJR–Algorithmus ein einzelnes Symbol (Bit) unter Berücksichtigung der gesamten empfangenen Codesequenz. Es handelt sich hierbei also um eine symbolweise Maximum–Aposteriori–Decodierung  ⇒  bit–wise MAP.

Der Unterschied zwischen Viterbi–Algorithmus und BCJR–Algorithmus soll – stark vereinfacht – am Beispiel eines terminierten Faltungscodes dargestellt werden:

• Der Viterbi–Algorithmus arbeitet das Trellis nur in einer Richtung – der Vorwärtsrichtung – ab und berechnet für jeden Knoten die Metriken ${\it \Lambda}_i(S_{\mu})$. Nach Erreichen des Endknotens wird der überlebende Pfad gesucht, der die wahrscheinlichste Codesequenz kennzeichnet.
  

• Beim BCJR–Algorithmus wird das Trellis zweimal abgearbeitet, einmal in Vorwärtsrichtung und anschließend in Rückwärtsrichtung. Für jeden Knoten sind dann zwei Metriken angebbar, aus denen für jedes Bit die Aposterori–Wahrscheinlichkeit bestimmt werden kann.
  
  

Hinweis: Diese Kurzzusammenfassung basiert auf dem Lehrbuch [Bos98]. Eine etwas ausführlichere Beschreibung des BCJR–Algorithmus' folgt im Kapitel 4.1.

Aufgaben zum Kapitel

A3.9 Viterbi–Algorithmus: Grundlegendes

A3.10 Fehlergrößenberechnung

A3.11 Viterbi–Pfadsuche