Exercise 1.6: (7, 4) Hamming Code
1962 hat Richard Wesley Hamming eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl m der zugeführten Prüfbits unterscheiden. Die Codewortlänge ist bei diesen Codes stets $n = 2^m – 1$ und das Informationswort besteht aus $k = n – m$ Bit:
- m = 2: (3, 1) Hamming–Code, ⇒ RC (3, 1),
- m = 3: (7, 4) Hamming–Code,
- m = 4: (15, 11) Hamming–Code,
- m = 5: (31, 26) Hamming–Code, usw.
Im Verlaufe dieser Aufgabe gibt es Fragen
- zum Codeumfang |C|,
- zur Coderate R, und
- zur minimalen Distanz $d_{\rm min}$
dieser Codeklasse. Weiterhin soll geklärt werden, ob der für diese Aufgabe durch seine Codetabelle $\underline{u}_{\rm i} ⇒ \underline{x}_{\rm i}$ gegebene (7, 4)–Hamming–Code systematisch ist, und ob es sich um einen
so genannten „perfekten Code” handelt. Der Laufindex kann hierbei die Werte $i = 1, ... , 2^k =16$ annehmen.
Hinweis :
Die Aufgabe bezieht sich auf das Kapitel Beispiele binärer Blockcodes. Genaueres zu den Hamming–Codes finden Sie auf folgenden Seiten:
Für diesen Hamming–Code wurden andere Prüfgleichungen herangezogen als im Theorieteil. Deshalb unterscheiden sich auch die Codetabellen. In der Aufgabe 1.07, bei der der gleiche Code verwendet wird, ist das Schaubild der Prüfgleichungen angegeben.
Man spricht von einem perfekten Code, wenn folgende Bedingung erfüllt ist:
- $$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
Hierbei bezeichnet t die Anzahl der korrigierbaren Fehler. Bei ungerader Minimaldistanz $d_{rm\ min}$ gilt:
- $$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$
Die Interpretation zu dieser Bedingung finden Sie in der Musterlösung zu dieser Aufgabe.
Fragebogen
Musterlösung
(2) Jedes Codewort x beinhaltet zunächst die $k = 4$ Bit des Informationswortes u. Danach folgen $m = 3$ Prüfbits:
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$
Dies entspricht genau der Definition eines systematischen Codes ⇒ JA.
(3) Bei jedem Hamming–Code beträgt die minimale Distanz $d_{\rm min} \underline{= 3}$. Aus der Tabelle erkennt man dies daran, dass das minimale [[|Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_BlockcodierungHamming–Gewicht] (die Anzahl der Einsen in einem Codewort) gleich 3 ist. Ein linearer Code beinhaltet nämlich auch das Nullwort, so dass gilt:
- $$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} }\hspace{0.1cm}w_{\rm H}(\underline{x}) = 3 \hspace{0.05cm}.$$
(4) Die Angabe $d_{\rm min} = 3$ bedeutet, dass $\underline{e = 2}$ Fehler erkannt und $\underline{t = 1}$ Fehler korrigiert werden können.
(5) Die Bedingung für einen perfekten Code lautet entsprechend der Angabe:
- $$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
Beim hier betrachteten (7, 4)–Hamming–Code gilt $n = 7$, $m = 3$ und $t = 1$, so dass sich auf beiden Seiten der Gleichung der Wert 8 ergibt ⇒ JA:
- $$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$
(6) Richtig sind nur die beiden letzten Aussagen. Gäbe es einen Kanalcode, der für alle Kanäle die Blockfehlerwahrscheinlichkeit bei endlicher Codewortlänge n zu Null macht, so wäre dieser nicht nur perfekt, sondern ein Wunder. Aufgrund des Kanalcodierungstheorems ist aber Pr(Blockfehler) $= 0$ bei endlichem n gar nicht möglich.
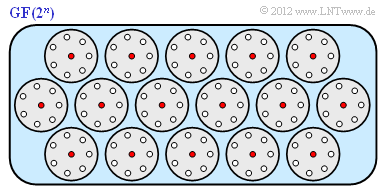
Veranschaulichen wir uns die Aussage 2 durch die obige Grafik. Der hochdimensionale Raum ist hierbei stark vereinfacht (in 2D) dargestellt. Wir gehen dabei von den Zahlenwerten $k = 4$, $n = 7$, $m = 3$, $t = 1$ des (7, 4, 3)–Hamming–Codes aus:
- Für das Empfangswort sind $2^7 = 128$ Punkte im 7–dimensionalen Raum möglich. Die roten Punkte markieren die $2^4 = 16$ gültigen Codeworte.
- Die Kreise umfassen jeweils 8 Punkte, nämlich ein gültiges Codewort und $n = 7$ Empfangsworte nach nur einem Fehler, die man bei der Decodierung genau diesem Codewort zuordnet.
- Insgesamt gibt es $2^4 = 16$ solcher Kreise. Wegen $128 = 16 · 8$ liegt deshalb kein einziges Empfangswort y außerhalb eines solchen Zuordnungskreises.
Auch die letzte Aussage ist zutreffend, was beispielhaft für $d_{\rm min} = 4$ gezeigt werden soll. Hiermit kann ebenfalls nur $t = 1$ Fehler korrigiert werden. Unterscheidet sich ein Empfangswort y von zulässigen Codeworten in 2 Bit, so ist dieser Punkt keinem Kreis zuzuordnen. Es liegen dann auch Punkte außerhalb der Kreise und die Bedingung eines perfekten Codes ist nicht mehr erfüllt.
(7) Richtig sind die Aussagen 1, 2, 3 und 5. Alle Hamming–Codes haben die minimale Hamming–Distanz $d_{\rm min} = 3 ⇒ t = 1$. Gleichzeitig lässt sich jeder (n, k)–Hamming–Code auch als $(2^m – 1, 2^m – 1 – m)$ Code schreiben, wobei $m = n – k$ die Anzahl der Prüfbits angibt. Damit wird die Gleichung eines perfekten Codes stets erfüllt:
- $${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$
Hierbei bedeuten:
m = 2: (3, 1)–Hamming–Code, identisch mit dem Repetition Code (3, 1),
m = 3: (7, 4)–Hamming–Code,
m = 4: (15, 11)–Hamming–Code,
m = 5: (31, 26)–Hamming–Code,
m = 6: (63, 57)–Hamming–Code.
Auch der Wiederholungscode mit $n = 5$ erfüllt die Bedingung. Mit $d_{\rm min} = 5$, $t = 2$ und $m = 4$ erhält man:
- $${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$
Die anderen Wiederholungscodes (RC) mit ungeradem n sind ebenfalls perfekt, nicht jedoch RC (4, 1), RC (6, 1), usw. Dies wurde bereits in der Musterlösung zur Teilaufgabe 6) begründet.