Exercise 4.1Z: Log Likelihood Ratio at the BEC Model

BEC–Kanalmodell

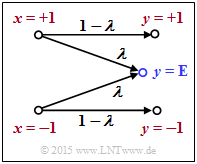
Wir betrachten das so genannte BEC–Kanalmodell (Binary Erasure Channel) mit

der Eingangsgröße $x ∈ \{+1, \, –1\}$,
der Ausgangsgröße $y ∈ \{+1, \, –1, \, {\rm E}\}$, und
der Auslöschungswahrscheinlichket $\lambda$.

Hierbei bedeutet $y = {\rm E}$ (Erasure), dass der Ausgangswert $y$ weder als „$+1$” noch als „$–1$” entschieden werden konnte.

Bekannt sind zudem die Eingangswahrscheinlichkeiten

$${\rm Pr}(x = +1) = 3/4\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(x = -1) = 1/4\hspace{0.05cm}.$$

Das Log–Likelihood–Verhältnis (kurz: $L$–Wert, englisch: Log Likelihood Ratio, LLR) der binären Zufallsgröße $x$ ist bei bipolarer Betrachtungsweise wie folgt gegeben:

$$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.$$

Entsprechend gilt für den bedingten $L$–Wert in Vorwärtsrichtung für alle $y ∈ \{+1, \, –1, \, {\rm E}\}$:

$$L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}. $$

Hinweis:

Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$L(x) \ = \ $

${\rm Pr}(x = \, –1) \ = \ $

$L(y = {\rm E} | x) \ = \ $

	$L(y = +1 \| x)$ ist positiv unendlich.
	$L(y = \, –1 \| x)$ ist negativ und betragsmäßig unendlich groß.
	Es gilt $L(y = +1 \| x) = L(y = \, –1 \| x) = 0$.

	Für $0 ≤ \lambda ≤ 1$.
	Für $0 < \lambda ≤ 1$.
	Für $0 ≤ \lambda < 1$.
	Für $0 < \lambda < 1$.

Musterlösung

Solution

(1)

(2)

(3)

(4)

(5)