Exercise 4.3Z: Conversions of L-value and S-value
From LNTwww
Funktion $y = \tanh {(x)}$ in Tabellenform
Wir gehen von einer binären Zufallsgröße $x ∈ \{+1, \, –1\}$ mit folgenden Wahrscheinlichkeiten aus:
- $${\rm Pr}(x =+1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} p\hspace{0.05cm},$$
- $${\rm Pr}(x =-1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} q = 1-p\hspace{0.05cm}.$$
Die „Zuverlässigkeit” des Symbols $x$ kann ausgedrückt werden
- durch den $L$–Wert entsprechend der Definition
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.05cm},$$
- durch den so genannten $S$–Wert
- $$S(x) = p- q \hspace{0.05cm}.$$
Den Begriff „$S$–Wert” haben wir kreiert, um die folgenden Fragen griffiger formulieren zu können. In der Literatur findet man hierfür manchmal die Bezeichung „Soft Bit”.
Wie in Teilaufgabe (1) gezeigt werden soll, können $L(x)$ und $S(x)$ ineinander umgerechnet werden.
Anschließend sollen diese Funktionen zur Berechnung der folgenden Größen berechnet werden, wobei stets von der Codelänge $n = 3$ ausgegangen wird:
- der extrinsische $L$–Wert für das dritte Symbol ⇒ $L_{\rm E}(x_3)$,
- der Aposteriori–$L$–Wert für das dritte Symbol ⇒ $L_{\rm APP}(x_3)$.
Die Berechnung soll für folgende Codes erfolgen:
- dem Wiederholungscode ⇒ RC (3, 1) mit der Nebenbedingung $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$,
- dem Single Parity–check Code ⇒ SPC (3, 2) mit der Nebenbedingung $x_1 \cdot x_2 \cdot x_3 = +1$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
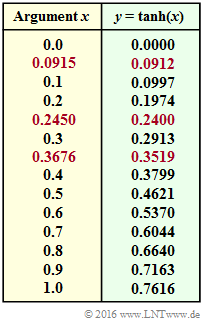
- Zur Lösung benötigen Sie den Tangens Hyperbolikus entsprechend folgender Definition:
- $$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} \hspace{0.05cm}.$$
- Diese Funktion ist oben in Tabellenform angegeben.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
