Exercise 1.09Z: Extension and/or Puncturing

• Return to book

Zur Erweiterung und Punktierung

Häufig kennt man einen Code, der für eine Anwendung als geeignet erscheint, dessen Coderate aber nicht exakt mit den Vorgaben übereinstimmt.

Zur Ratenanpassung gibt es verschiedene Möglichkeiten

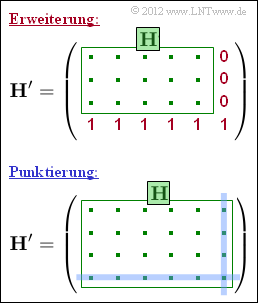
• $\color{red}{\boldsymbol{\rm Erweiterung}}$ (englisch Extension): Ausgehend vom $(n, k)$–Code, dessen Prüfmatrix H gegeben ist, erhält man einen $(n+1, k)$–Code, indem man die Prüfmatrix um eine Zeile und eine Spalte erweitert und die neuen Matrixelemente entsprechend der oberen Grafik mit Nullen und Einsen ergänzt. Man fügt ein neues Prüfbit

$$x_{n+1} = x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n$$

hinzu und damit auch eine neue Prüfgleichung, die in H' berücksichtigt ist.

• $\color{red}{\boldsymbol{\rm Punktierung}}$ (englisch Puncturing): Entsprechend der unteren Abbildung kommt man zu einem $(n–1, k)$–Code größerer Rate, wenn man auf ein Prüfbit und eine Prüfgleichung verzichtet, was gleichbedeutend damit ist, aus der Prüfmatrix H eine Zeile und eine Spalte zu streichen.

• $\color{red}{\boldsymbol{\rm Verkürzung}}$ (englisch Shortening): Verzichtet man anstelle eines Prüfbits auf ein Informationsbit, so ergibt sich ein $(n–1, k–1)$–Code kleinerer Rate.

In dieser Aufgabe sollen ausgehend von einem (5, 2)–Blockcode

$$\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.1cm}, (0, 1, 0, 1, 1) \hspace{0.1cm},(1, 0, 1, 1, 0) \hspace{0.1cm},(1, 1, 1, 0, 1) \}$$

folgende Codes konstruiert und analysiert werden:

• ein (6, 2)–Code durch einmalige Erweiterung,

• ein (7, 2)–Code durch nochmalige Erweiterung,

• ein (4, 2)–Code durch Punktierung.

Die Prüfmatrix und die Generatormatrix des systematischen (5, 2)–Codes lauten:

$${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.3cm} \Leftrightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Hinweis :

Die Aufgabe bezieht sich auf das Kapitel Allgemeine Beschreibung linearer Blockcodes. In der Aufgabe 1.09 wird beispielhaft gezeigt, wie aus dem (7, 4, 3)–Hamming–Code durch Erweiterung ein (8, 4, 4)–Code entsteht.

Fragebogen

1

Geben Sie die Kenngrößen des vorgegebenen (5, 2)–Codes an.

$\ (5, 2)–{\rm Code}: R $ =

$\ d_{\rm mim}$=

2

Welche Codeworte besitzt der (6, 2)–Code nach Erweiterung?

	$(0 0 0 0 0 1), (0 1 0 1 1 0), (1 0 1 1 0 0), (1 1 1 0 1 1).$
	$(0 0 0 0 0 0), (0 1 0 1 1 1), (1 0 1 1 0 1), (1 1 1 0 1 0).$

3

Geben Sie die Kenngrößen des erweiterten (6, 2)–Codes an.

$\ (6, 2)–{\rm Code}: R $ =

$\ d_{\rm mim}$=

4

Wie lautet die systematische Generatormatrix des (7, 2)–Codes?

	Zeile 1 von ${\boldsymbol{\rm G}}: 1, 0, 1, 1, 0, 1, 0.$
	Zeile 2 von ${\boldsymbol{\rm G}}: 0, 1, 0, 1, 1, 1, 0.$

5

Geben Sie die Kenngrößen des erweiterten (7, 2)–Codes an.

$\ (7, 2)–{\rm Code}: R $ =

$\ d_{\rm mim}$=

6

Welche Aussagen gelten für den (4, 2)–Code (Punktierung des letzten Prüfbits)?

	Die Coderate beträgt nun $R = 2/4 = 0.5.$
	$C_{(4, 2)} = {(0, 0, 0, 0), (1, 0, 1, 1), (0, 1, 0, 1), (1, 1, 1, 0)}.$
	Die Minimaldistanz bleibt gegenüber dem (5, 2)–Code gleich.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.