Exercise 4.4Z: Supplement to Exercise 4.4

Hamming–Gewicht und Wahrscheinlichkeiten

Der Informationstheoretiker Robert G. Gallager hat sich bereits 1963 mit folgender Fragestellung beschäftigt:

Gegeben ist ein Zufallsvektor $\underline{x} = (x_1, \, x_2, \ ... \ , \, x_n)$ mit $n$ binären Elementen $x_i ∈ \{0, \, 1\}$ .
Bekannt sind alle Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ und $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ mit Inex $i = 1, \ ... \ , \ n$ .
Gesucht ist die Wahrscheinlichkeit, dass die Anzahl der Einsen in diesem Vektor geradzahlig ist.
Oder ausgedrückt mit dem Hamming–Gewicht: Wie groß ist die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$ ?

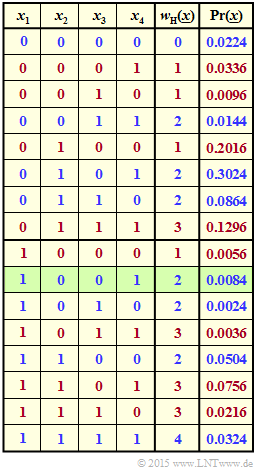
Die Grafik verdeutlicht die Aufgabenstellung für das Beispiel $n = 4$ sowie $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3$ und $p_4 = 0.6$ .

Für die grün hinterlegte Zeile ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ gilt $w_{\rm H}(\underline{x}) = 2$ und ${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084$ .
Blaue Schrift bedeutet ein geradzahliges Hamming–Gewicht. Rote Schrift steht für „ $w_{\rm H}(\underline{x})$ ist ungerade”.
Die Wahrscheinlichkeite ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$ ist gleich der Summe der blauen Zahlen in der letzten Spalte. Die Summe der roten Zahlen ergibt ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ ungerade}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x} {\rm \ ist \ gerade}]$ .

Gallager hat das Problem in analytischer Weise gelöst:

$\hspace{0.2cm} {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$

${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$

Fragebogen

Musterlösung

Solution

(1) (2) (3) (4) (5)

	correct
	false