Exercise 1.13: Binary Erasure Channel Decoding

• Return to book

Zur BEC–Decodierung

Wir gehen hier von dem Modell auf der letzten Theorieseite im Kapitel 1.5 aus (grün hinterlegte BEC–Konfiguration):

• Jedes Informationswort $\underline{u}$ wird blockweise codiert und liefert das Codewort $\underline{x}$. Der Blockcode sei linear und durch seine Prüfmatrix $\boldsymbol{\rm H}$ vollständig gegeben.

• Bei der Übertragung werden $n_{\rm E}$ Bit des Codewortes ausgelöscht ⇒ Binary Erasure Channel (BEC). Aus dem Codewort $\underline{x}$ wird somit das Empfangswort $\underline{y}$.

• Ist die Anzahl $n_{\rm E}$ der Auslöschungen kleiner als die minimale Distanz $d_{\rm min}$ des Codes, so gelingt es, aus $\underline{y}$ das Codewort $\underline{z} = \underline{x}$ ohne Fehler zu rekonstruieren, und man erhält so auch das richtige Informationswort $\underline{\upsilon} = \underline{u}$.

• Zur Aufgabenbeschreibung betrachten wir beispielhaft das Hamming–Codewort $\underline{x} = (0, 1, 0, 1, 1, 0, 0)$ und das Empfangswort $\underline{y} = (0, 1, {\rm E} , {\rm E}, 1, 0, 0).$

Ausgelöscht wurden somit durch den Kanal das dritte und vierte Bit. Der Codewortfinder hat somit die Aufgabe, den Vektor $z_{\rm E} = (z_{3}, z_{4})$ mit $z_{3}, z_{4} \in$ {0, 1} zu bestimmen. Dies geschieht entsprechend der Gleichung

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm},$$

wobei im vorliegenden Beispiel gilt:

$$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$

Diese Gleichung liefert zwei Bestimmungsgleichungen für die zu bestimmenden Bits, deren Lösung zum Ergebnis $z_{3} = 0$ und $z_{4} = 1$ führt.

Hinweis:

Die Aufgabe gehört zu Kapitel Decodierung linearer Blockcodes Der Algorithmus zur Zuordnung des Empfangswortes $\underline{y}$ zum richtigen Codewort $\underline{z} = \underline{x}$ ist im Theorieteil ausführlich beschrieben. Wir möchten nochmals daran erinnern, dass wir bei der BEC–Decodierung den ersten Decoderblock $\underline{y} → \underline{z}$ als Codewortfinder bezeichnen, da hier Fehlentscheidungen ausgeschlossen sind. Jedes Empfangswort wird richtig decodiert, oder es kann gar nicht decodiert werden. Beim BSC–Modell lassen sich dagegen Decodierfehler nicht vermeiden. Dementsprechend heißt der entsprechende Block dort Codewortschätzer.

Fragebogen

1

Empfangen wurde $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Für welche Sequenz entscheidet sich der Codewortschätzer?

	$\underline{z} \ = \ (1, 0, 0, 1, 0, 0, 0),$
	$\underline{z} \ = \ (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} \ = \ (1, 0, 0, 1, 0, 0, 1).$

2

Welche Konsequenzen ergeben sich aus den roten Eintragungen für $\boldsymbol{\rm H}_{\rm K}$ und $z_{\rm K}$ (siehe Grafik auf der Angabenseite)?

	Der Erasure–Vektor lautet $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}).$
	Das Empfangswort lautet $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm E}$ ist eine 2 x 3–Matrix.
	$\boldsymbol{\rm H}_{\rm E}$ ist eine 3 x 3–Matrix.

3

Nun gelte $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$ Welches Codewort wird ausgewählt?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	Für das vorliegende y ist keine eindeutige Decodierung möglich.

4

Welche Konsequenzen ergeben sich aus den grünen Eintragungen für $\boldsymbol{\rm H}_{\rm K}$ und $z_{\rm K}$ (siehe Grafik auf der Angabenseite)?

	Das Empfangswort lautet $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm K}$ unterscheidet sich gegenüber Teilfrage (2) in der letzten Zeile.
	$\boldsymbol{\rm H}_{\rm K}$ unterscheidet sich gegenüber Teilfrage (2) in der letzten Spalte.

5

Nun gelte $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$ Welches Codewort wird ausgewählt?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	Für das vorliegende $\underline{y}$ ist keine eindeutige Decodierung möglich.

6

Welche Aussagen ergeben sich für die Korrekturfähigkeit beim BEC? $n_{\rm E}$ gibt dabei Anzahl der Auslöschungen (Erasures) an.

	Für $n_{\rm E} \ < \ d_{\rm min}$ ist stets eine eindeutige Decodierung möglich.
	Für $n_{\rm E} \ = \ d_{\rm min}$ ist stets eine eindeutige Decodierung möglich.
	Für $n_{\rm E} \ = \ d_{\rm min}$ ist manchmal eine eindeutige Decodierung möglich.
	Für $n_{\rm E} \ >\ d_{\rm min}$ ist eine eindeutige Decodierung nie möglich.

Musterlösung

Solution

(1)  Der Empfangsvektor lautet $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Ausgelöscht wurden also die Codesymbole an den Positionen 2 und 7. Ausgehend von der vorgegebenen Prüfmatrix

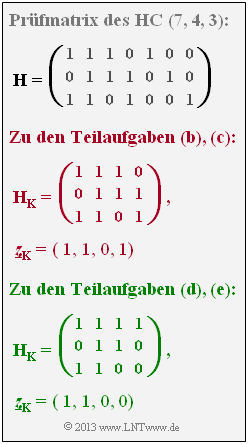
$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}$$

des Hammingcodes erhält man für Vektor und Matrix hinsichtlich

• aller $\color{red}{\boldsymbol{\rm korrekt \ übertragenen \ Codesymbole}}$ (Index K), die dem Codewortfinder bekannt sind:

$$\underline{z}_{\rm K} = (1, 0, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \hspace{0.05cm},$$

• hinsichtlich der beiden $\color{red}{\boldsymbol{\rm ausgelöschten \ Codesymbole}}$ $z_{2}$ und $z_{7}$ (Index E), die zu ermitteln sind:

$$\underline{z}_{\rm E} = (z_2, z_7)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Die Bestimmungsgleichung lautet somit:

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}$$

$$\Rightarrow \hspace{0.3cm} \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_7 \end{pmatrix} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm}.$$

Daraus ergeben sich drei Gleichungen für die beiden Unbekannten $z_{2}$ und $z_{7}$:

(a) $z_{2} = 1$, (b) $z_{2} = 1$, (c) $z_{2} + z_{7} = 0 ⇒z_{7}= 1$.

Somit liefert der Codewortfinder $\underline{z} = (1, 1, 0, 1, 0, 0, 1)$ ⇒ Lösungsvorschlag 2.

(2)  Betrachtet man die vorgegebene Matrix $\boldsymbol{\rm H}_{\rm K}$, so erkennt man, dass diese mit dem ersten vier Spalten der Prüfmatrix $\boldsymbol{\rm H}$ übereinstimmt. Die Auslöschungen betreffen also die letzten 3 Bit des Empfangswortes ⇒ $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}) ⇒ \underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$ und die Erasure–Matrix lautet:

$${ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

Richtig sind demzufolge die Aussagen 1, 2 und 4.

(3)  Man erhält nach einigen Matrizenmultiplikationen:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0\\ 0 &1 &1 &1\\ 1 &1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm},$$

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} \hspace{0.05cm}.$$

Durch Gleichsetzen folgt $z_{5} = 0, z_{6} = 0, z_{7} = 1$ ⇒ Lösungsvorschlag 2.

(4)  Der Matrizenvergleich zeigt, dass die ersten drei Spalten von $\boldsymbol{\rm H}$ und $\boldsymbol{\rm H}_{\rm K}$ identisch sind. Die vierte Spalte von $\boldsymbol{\rm H}_{\rm K}$ ist gleich der fünften Spalte der Prüfmatrix. Daraus folgt für den Vektor $z_{\rm E} = (z_{4}, z_{6}, z_{7})$ und weiter für den Empfangsvektor $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$ ⇒ Lösungsvorschlag 1 und 3.

(5)  Analog zur Teilaufgabe (3) erhält man nun:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &1\\ 0 &1 &1 &0\\ 1 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm},$$

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 0 &0 &0\\ 1 &1 &0\\ 1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_4 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} 0 \\ z_4 + z_6 \\ z_4 + z_7 \end{pmatrix} \hspace{0.05cm}.$$

Setzt man nun die beiden Spaltenvektoren gleich, so erhält man nur mehr zwei Gleichungen für die drei Unbekannten ⇒ Lösungsvorschlag 4. Oder anders ausgedrückt: Ist die Anzahl der Auslöschungen des BEC–Kanals größer als der Rang der Matrix $\boldsymbol{\rm H}_{\rm E}$, so ergibt sich keine eindeutige Lösung des resultierenden Gleichungssystems.

(6)  Zur Lösung dieser Aufgabe beziehen wir uns wieder auf den systematischen Hamming–Code $(7, 4, 3)$ entsprechend der angegebenen Prüfgleichung und der nachfolgenden Codetabelle. Die Informationsbit sind schwarz dargestellt und die Prüfbit rot. Die minimale Distanz dieses Codes beträgt $d_{\rm min} = 3$.

Codetabelle des systematischen (7, 4, 3)–Hamming–Codes

Weiter nehmen wir an, dass stets das gelb hinterlegte Codewort $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ gesendet wurde:

• Ist die Anzahl $n_{\rm E}$ der Auslöschungen kleiner als $d_{\rm min} = 3$, so ist eine Decodierung nach der hier beschriebenen Methode immer möglich ⇒ siehe beispielsweise Teilaufgabe (1) mit $n_{E }= 2$.

• Auch für $n_{\rm E} = d_{\rm min} = 3$ ist manchmal eine Decodierung möglich, wie in Aufgabe (3) gezeigt. In der Codetabelle gibt es nur ein einziges Codewort, das zum Empfangsvektor $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$ passen könnte, nämlich das gelb hinterlegte Codewort $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$.

• Dagegen konnte $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$ entsprechend Teilaufgabe (4) nicht decodiert werden. In der Codetabelle erkennt man neben (1, 1, 0, 1, 0, 0, 1) mit (1, 1, 0, 0, 0, 1, 0) ein weiteres Codewort (grün hinterlegt), das durch die $n_{\rm E} = 3$ gegebenen Auslöschungen zum Empfangswort $\underline{y}$ wird. Dieser Fall, wenn die $n_{\rm E} = d_{\rm min}$ Auslöschungen genau die dmin unterschiedlichen Bit zweier Codeworte betreffen, führt zu einer Matrix HE mit einem Rang kleiner als dmin.

• Ist $\boldsymbol{\rm H}_{\rm E} > d_{\rm min}$, so ist die Anzahl $n – n_{\rm E}$ der nicht ausgelöschten Bit kleiner als die Anzahl $k$ der Informationsbit. In diesem Fall kann das Codewort natürlich nicht decodiert werden.

Das heißt: Zutreffend sind die Aussagen 1, 3 und 4.