Exercise 1.6Z: Ergodic Probabilities

• Return to book

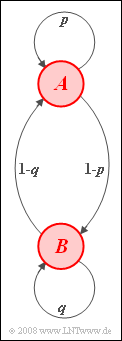
Wir betrachten eine homogene stationäre Markovkette erster Ordnung mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten entsprechend dem nebenstehenden Markovdiagramm:

Für die Teilaufgaben (1) bis (4) wird vorausgesetzt:

• Nach dem Ereignis $A$ folgen $A$ und $B$ mit gleicher Wahrscheinlichkeit.

• Nach $B$ ist das Ereignis $A$ doppelt so wahrscheinlich wie $B$.

Ab Teilaufgabe (5) sind $p$ und $q$ als freie Parameter zu verstehen, während die Ereigniswahrscheinlichkeiten ${\rm Pr}(A) = 2/3$ und ${\rm Pr}(B) = 1/3$ fest vorgegeben sind.

Hinweise:

• Die Aufgabe gehört zum Kapitel Markovketten.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Sie können Ihre Ergebnisse mit dem nachfolgenden Berechnungstool überprüfen:

Ereigniswahrscheinlichkeiten einer Markovkette 1. Ordnung

Fragebogen

1

Wie groß sind die Übergangswahrscheinlichkeiten $p$ und $q$?

$p \ =$

$q \ =$

2

Berechnen Sie die ergodischen Wahrscheinlichkeiten.

${\rm Pr}(A) \ =$

${\rm Pr}(B) \ =$

3

Wie groß ist die bedingte Wahrscheinlichkeit, dass das Ereignis $B$ auftritt, wenn zwei Takte vorher das Ereignis $A$ aufgetreten ist?

${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})\ =$

4

Wie groß ist die Rückschlusswahrscheinlichkeit, dass zwei Takte vorher das Ereignis $A$ aufgetreten ist, wenn aktuell $B$ auftritt?

${\rm Pr}(A_{\nu-2}\hspace{0.05cm}|\hspace{0.05cm}B_{\nu})\ =$

5

Es gelte nun $p = 1/2$ und ${\rm Pr}(A) = 2/3$. Welcher Wert ergibt sich für $q$?

$q\ =$

6

Wie muss man die Parameter wählen, damit die Folgenelemente der Markovkette statistisch unabhängig sind und zusätzlich ${\rm Pr}(A) = 2/3$ gilt?

$p \ =$

$q \ =$

Musterlösung

Solution

(1)  Gemäß der Angabe gilt $p = 1 - p$,   ⇒   $\underline{p =1/2}$, und $q = (1 - q)/2$,   ⇒   $\underline{q =1/3}$.

(2)  Für die Ereigniswahrscheinlichkeit von $A$ gilt:

$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$

Damit ergibt sich ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$.

(3)  Über den Zeitpunkt $\nu-1$ ist keine Aussage getroffen. Zu diesem Zeitpunkt kann $A$ oder $B$ aufgetreten sein. Deshalb gilt:

$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) = \frac{5}{12} \hspace{0.15cm}\underline {\approx 0.417}.$$

(4)  Nach dem Satz von Bayes gilt:

$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$

Die Wahrscheinlichkeit ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$ wurde bereits im Unterpunkt (3) berechnet. Aufgrund der Stationarität gilt ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$ und ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$. Damit erhält man für die gesuchte Rückschlusswahrscheinlichkeit nach obiger Gleichung den Wert 5/9.

(5)  Entsprechend der Teilaufgabe (2) gilt mit ${p =1/2}$ für die Wahrscheinlichkeit von $A$ allgemein:

$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$

Aus ${\rm Pr}(A) = 2/3$ folgt somit $\underline{q =0}$.

(6)  Im Fall der statistischen Unabhängigkeit muss beispielsweise gelten:

$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$

Daraus folgt $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$ und dementsprechend $q = 1-p \hspace{0.15cm}\underline {= 1/3}$.