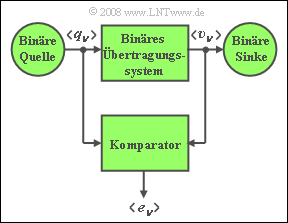
Exercise 3.7: Bit Error Rate (BER)
Wir betrachten ein binäres Übertragungssystem mit
- der Quellensymbolfolge $\langle q_\nu \rangle $ und
- der Sinkensymbolfolge $\langle v_\nu \rangle $.
Stimmen Sinkensymbol $v_\nu$ und Quellensymbol $q_\nu$ nicht überein, so liegt ein Bitfehler vor ⇒ $e_\nu = 1$ Ansonsten gilt $e_\nu = 0$.
Wichtigstes Beurteilungskriterium eines solchen Digitalsystems ist die Bitfehlerwahrscheinlichkeit (englisch: Bit Error Probability).
Mit dem Erwartungswert ${\rm E}[ ... ]$ ist diese ist wie folgt definiert:
$$\it p_{\rm B} = \rm E[\rm Pr(\it v_{\nu} \ne q_{\nu} \rm )]=\rm E[\rm Pr(\it e_{\nu}=\rm 1)]=\lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm Pr(\it e_{\nu}=\rm 1).$$
Der rechte Teil dieser Gleichung beschreibt eine Zeitmittelung und muss z. B. bei zeitvarianten Kanälen stets angewandt werden. Ist dagegen die Fehlerwahrscheinlichkeit für alle Symbole gleich (was hier vorausgesetzt werden soll), so kann man die obige Gleichung wie folgt vereinfachen: $$\it p_{\rm B} = \rm E[\rm Pr(\it e_{\nu}=\rm 1)]=\rm E[\it e_{\nu} \rm ].$$
Die Bitfehlerwahrscheinlichkeit ist eine A-priori-Kenngröße, erlaubt also eine Vorhersage für das zu erwartende Resultat. Dagegen muss zur messtechnischen Ermittlung der Übertragungsqualität oder bei der Systemsimulation auf die vergleichbare A-posteriori-Kenngröße Bitfehlerquote (englisch: Bit Error Rate) übergegangen werden:
- $$h_{\rm B}=\frac{n_{\rm B}}{N}=\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu}.$$
Diese ist eine relative Häufigkeit, wobei $n_{\rm B}$ die Anzahl der aufgetretenen Bitfehler angibt, wenn insgesamt $N$ Symbole (Bit) übertragen wurden.
- Im Grenzfall $N \to \infty$ stimmt die relative Häufigkeit $h_{\rm B}$ mit der Wahrscheinlichkeit $p_{\rm B}$ überein.
- Hier soll nun die Frage geklärt werden, mit welcher statistischen Unsicherheit bei endlichem N gerechnet werden muss.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gaußverteilte Zufallsgröße.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Lösen Sie die Aufgaben so weit wie möglich allgemein. Verwenden Sie zur Kontrolleingabe die Parameterwerte $p_{\rm B} = 10^{-3}$ und $N = 10^{5}$.
- Nachfolgend finden Sie einige Werte der sogenannten Q-Funktion:
- $$\rm Q(\rm 1.00)=\rm 0.159,\hspace{0.5cm}\rm Q(\rm 1.65)=\rm 0.050,\hspace{0.5cm}\rm Q(\rm 1.96)=\rm 0.025,\hspace{0.5cm}\rm Q(\rm 2.59)=\rm 0.005.$$
Fragebogen
Musterlösung
- Bezüglich der Zufallsgröße $n_{\rm B}$ liegt der klassische Fall einer Binomialverteilung vor.
- Es wird die Summe über $N$ binäre Zufallsgrößen gebildet.
- Die möglichen Werte von $n_{\rm B}$ liegen somit zwischen $0$ und $N$.
- Der lineare Mittelwert ergibt $m_{n{\rm B}}=p_{\rm B}\cdot N=\rm 10^{-3}\cdot 10^{5}=\rm 100.$
(2) Für die Streuung der Binomialverteilung gilt mit guter Näherung:
$$\sigma_{n{\rm B}}=\sqrt{N\cdot p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}
\hspace{0.15cm}\underline{\approx 10}.$$
(3) Mögliche Werte von $h_{\rm B}$ sind alle ganzzahligen Vielfachen von $1/N$. Diese liegen zwischen $0$ und $1$ liegen. Für den Mittelwert erhält man: $$m_{h{\rm B}}=m_{n{\rm B}}/N=p_{\rm B} = 10^{-3}.$$
Die Streuung ergibt sich zu $$\sigma_{h{\rm B}}=\frac{\sigma_{n{\rm B}}}{N}=\sqrt{\frac{p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}{N}}\hspace{0.15cm}\underline{\approx \rm 10^{-4}}.$$
(4) Richtig ist der erste Vorschlag. Es gilt: $${\rm Pr}(h_{\rm B} > p_{\rm B} + \varepsilon)=\rm Q({\it\varepsilon}/{\it\sigma_{h{\rm B}}}),\hspace{0.5cm}\rm Pr(\it h_{\rm B} < p_{\rm B} - \varepsilon {\rm )}=\rm Q(\it{\varepsilon}/{\sigma_{h{\rm B}}}{\rm )}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\rm Pr(\it |h_{\rm B} - p_{\rm B}| \le \varepsilon \rm )=\rm 1-\rm 2\cdot \rm Q({\it \varepsilon}/{\it \sigma_{h{\rm B}}}).$$
(5) Man erhält mit den Zahlenwerten$\varepsilon = \sigma_{h{\rm B}} = 10^{-4}$: $$p_{\varepsilon}=\rm 1-\rm 2\cdot \rm Q(\frac{\rm 10^{\rm -4}}{\rm 10^{\rm -4}} {\rm )}=\rm 1-\rm 2\cdot\rm Q(\rm 1)\hspace{0.15cm}\underline{\approx\rm 0.684}.$$
Das heißt: Bestimmt man die Bitfehlerquote per Simulation über $10^5$ Symbole, so erhält man mit einem Konfidenzniveau von 68.4% einen Wert zwischen $0.9 \cdot 10^{-3}$ und $1.1 \cdot 10^{-3}$, wenn $p_{\rm B} = 10^{-3}$ ist.
(6) Aus der Beziehung $p_{\varepsilon}=\rm 1-\rm 2\cdot {\rm Q}(\alpha) = 0.95$ folgt direkt: $$\alpha_{\rm min}=\rm Q^{\rm -1}\Big(\frac{\rm 1-\it p_{\varepsilon}}{\rm 2}\Big)=\rm Q^{\rm -1}(\rm 0.025)\hspace{0.15cm}\underline{=\rm 1.96}\hspace{0.15cm}{\approx\rm 2}.$$
(7) Es muss $\alpha = \varepsilon/\sigma_{h{\rm B}}$ gelten. Mit dem Ergebnis der Teilaufgabe (2) folgt dann: $$\frac{\varepsilon}{\sqrt{p_{\rm B}\cdot(\rm 1-\it p_{\rm B})/N}}\ge {\rm 2} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} N\ge \frac{\rm 4\cdot \it p_{\rm B}\cdot(\rm 1-\it p_{\rm B})}{\varepsilon^{\rm 2}}\approx \frac{\rm 4\cdot 10^{-3}}{10^{-8}}\hspace{0.15cm}\underline{=\rm 400000}.$$