Exercise 5.8Z: Cyclic Prefix and Guard Interval

• Return to book

Zyklisches Präfix,
Guard-Intervall und Ausgangssysmbol

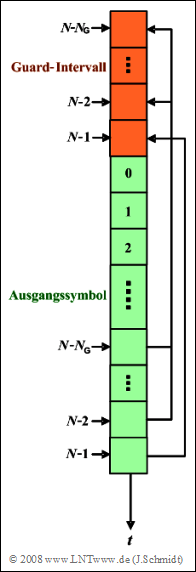
Wir gehen in dieser Aufgabe von einem OFDM–System mit $N = 8$ Trägern und zyklischem Präfix aus. Der Subträgerabstand sei $f_0 = 4 \ \rm kHz$. Die Grafik zeigt das Prinzip des zyklischen Präfixes.

• Die Übertragung erfolgt über einen Zweiwegekanal, wobei beide Pfade verzögert sind. Die Kanalimpulsantwort lautet somit mit $τ_1 = \ \rm 50 μs$ und $τ_2 = 125\ \rm μs$:

$$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$

• Der Einsatz eines solchen zyklischen Präfixes vermindert allerdings die Bandbreiteneffizienz (Verhältnis von Symbolrate zu Bandbreite) um den Faktor

$$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$

und führt auch zu einer Verringerung des Signal–Rausch–Verhältnisses um ebenfalls diesen Wert β.

• Voraussetzung für die Gültigkeit des hier angegebenen SNR–Verlustes ist allerdings, dass die Impulsantworten $g_{\rm S}(t)$ und $g_{\rm E}(t)$ von Sende– und Empfangsfilter an die Symboldauer $T$ angepasst sind (Matched–Filter–Ansatz).

Hinweise:

• Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
• Bezug genommen wird insbesondere auf die Seiten Zyklisches Präfix sowie OFDM-System mit zyklischem Präfix.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Geben Sie die Kernsymboldauer $T$ an.

$T \ = \ $ $\ \rm μs$

2

Wie lang sollte das Guard–Intervall $T_{\rm G}$ mindestens sein?

$T_{\rm G}\ = \ $ $\ \rm μs$

3

Bestimmen Sie die resultierende Rahmendauer $T_{\rm R}$.

$T_{\rm R}\ = \ $ $\ \rm μs$

4

Welche Aussagen sind richtig? Durch eine Guardlücke, also das Nullsetzen des OFDM–Signals im Guard–Intervall, können

	Intercarrier–Interferenzen (ICI) unterdrückt werden,
	Impulsinterferenzen (ISI) unterdrückt werden.

5

Welche Aussagen sind richtig? Durch ein zyklisches Präfix, also durch eine zyklische Erweiterung des OFDM–Signals im Guard–Intervall, können

	Intercarrier–Interferenzen (ICI) unterdrückt werden,
	Impulsinterferenzen (ISI) unterdrückt werden.

6

Nennen Sie die jeweilige Anzahl der Abtastwerte für das Kernsymbol $(N)$, das Guard–Intervall $(N_{\rm G})$ und den gesamten Rahmen $(N_{\rm R})$.

$N \hspace{0.35cm} = \ $

$N_{\rm G} \ = \ $

$N_{\rm R} \ = \ $

7

Geben Sie unter der Vorraussetzung, dass lediglich der erste Träger mit dem Trägerkoeffizienten $-1$ verwendet wird, die Abtastwerte des Guard–Intervalls vor der Übertragung über den Kanal an.

$\text{Re}[d_{-1}] \ = \ $

$\text{Im}[d_{-1}] \ = \ $

$\text{Re}[d_{-2}] \ = \ $

$\text{Im}[d_{-2}] \ = \ $

$\text{Re}[d_{-3}] \ = \ $

$\text{Im}[d_{-3}] \ = \ $

$\text{Re}[d_{-4}] \ = \ $

$\text{Im}[d_{-4}] \ = \ $

8

Welche Bandbreiteneffizienz $\beta$ ergibt sich inklusive des Guard–Intervalls?

$\beta\ = \ $

9

Wie groß ist der damit verbundene SNR–Verlust $10 · \lg \ Δ_ρ$ (in dB) unter der Voraussetzung des Matched–Filter–Ansatzes?

$10 · \lg \ Δ_ρ \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Die Kernsymboldauer ist gleich dem Kehrwert des Trägerabstands  ⇒   $ T = {1}/{f_0} \hspace{0.15cm}\underline {= 250\,\,{\rm \mu s}}.$

(2)  Um Interferenzen zu vermeiden, ist die Dauer des Guard–Intervalls $T_{\rm G}$ mindestens so groß zu wählen wie die maximale Verzögerung (hier: $τ_2 = 125\ \rm μs$) des Kanals   ⇒   $ T_{\rm G} \hspace{0.15cm}\underline {= 125\,\,{\rm \mu s}}.$

(3)  Für die Rahmendauer gilt somit:  $ T_{\rm{R}} = T + T_{\rm G}\hspace{0.15cm}\underline {= 375\,\,{\rm \mu s}}.$

(4)  Richtig ist der Lösungsvorschlag 2:

• Durch eine Guardlücke geeigneter Länge können ausschließlich Impulsinterferenzen (ISI) vermieden werden.
• Die Lückendauer $T_{\rm G}$ muss dabei so groß gewählt werden, dass das aktuelle Symbol durch das Vorgängersymbol nicht beeinträchtigt wird.
• Im vorliegenden Beispiel muss $T_{\rm G}≥ 125\ \rm μs$ sein.

(5)  Beide Lösungsvorschläge sind zutreffend:

• Durch ein zyklisches Präfix geeigneter Länge werden zusätzlich auch Intercarrier–Interferenzen (ICI) unterdrückt.
• Es wird damit sichergestellt, dass für alle Träger innerhalb der Kernsymboldauer $T$ eine vollständige und unverfälschte Schwingung auftritt, auch wenn andere Träger aktiv sind.

(6)  Die Anzahl der Abtastwerte innerhalb des Kernsymbols ist gleich der Anzahl der Träger   ⇒   $\underline{N=8}$.
Wegen $T_{\rm G}= T/2$ gilt $N_{\rm G}\hspace{0.15cm}\underline {= 4}$ und damit $N_{\rm R} = N + N_{\rm G}\hspace{0.15cm}\underline {= 12}$.

(7)  Die Belegung des ersten Trägers (Frequenz $f_0$) mit dem Koeffizienten „–1” führt zu den Abtastwerten

$$d_0 = -1, \hspace{0.3cm}d_1 = -0.707 - {\rm j} \cdot 0.707, \hspace{0.3cm}d_2 = -{\rm j} ,\hspace{0.3cm} d_3 = +0.707 -{\rm j} \cdot 0.707, $$

$$d_4 = +1, \hspace{0.3cm}d_5 = +0.707 + {\rm j} \cdot 0.707, \hspace{0.3cm}d_6 = +{\rm j} ,\hspace{0.3cm} d_7 = -0.707 +{\rm j} \cdot 0.707. $$

Die zyklische Erweiterung liefert die zusätzlichen Abtastwerte $d_{-1} = d_7$,   $d_{-2} = d_6$,   $d_{-3} = d_5$ und   $d_{-4} = d_4$:

$$\underline{{\rm Re}[d_{-1}] = -0.707,\hspace{0.3cm}{\rm Im}[d_{-1}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-2}] = 0,\hspace{0.3cm} {\rm Im}[d_{-2}] = 1},$$

$$\underline{{\rm Re}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Im}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-4}] = 1,\hspace{0.3cm} {\rm Im}\{d_{-4}] = 0}.$$

(8)  Entsprechend der angegebenen Gleichung ist die Bandbreiteneffizienz gleich

$$\beta = \frac{1}{1 + {T_{\rm{G}}}/{T}} = \frac{1}{1 + ({125\,\,{\rm \mu s}})/({250\,\,{\rm \mu s}})} \hspace{0.15cm}\underline {= 0.667}.$$

(9)  Die Bandbreiteneffizienz $β = 2/3$ führt zu einem SNR–Verlust von

$$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$