Exercise 4.11Z: Code Rate from the Parity-check Matrix
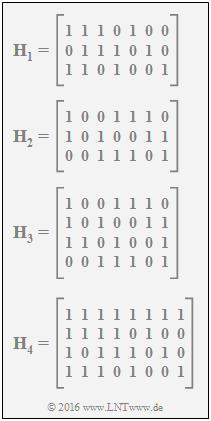
In dieser Aufgabe sollen die Coderaten der Codes $C_1, \, C_2, \, C_3$ und $C_4$ ermittelt werden, wobei die Codes allein durch ihre Prüfmatrizen gegeben sind. Eine untere Schranke für die Coderate $R$ lautet:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.05cm}.$$
Sind die $m$ Prüfgleichungen aller Matrix–Zeilen linear unabhängig, so gilt in obiger Ungleichung das Gleichheitszeichen.
Verwendet ist hier die folgende Nomenklatur:
- $w_{\rm Z}(j)$ mit $1 ≤ j ≤ m$ ist das Hamming–Gewicht der $j$–ten Zeile der Prüfmatrix.
- Durch Erwartungswertbildung ergibt sich:
- $${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} w_{\rm Z}(j)\hspace{0.05cm}.$$
- Entsprechend gibt $w_{\rm S}(i)$ mit $1 ≤ i ≤ n$ das Hamming–Gewicht der $i$–ten Spalte von $\mathbf{H}$ an, mit dem Erwartungswert
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} w_{\rm S}(i)\hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Themengebiet des Kapitels Grundlegendes zu den Low–density Parity–check Codes
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(2) Die Coderate des (7, 4, 3)–Hamming–Codes ist $\underline{R = 4/7 = 0.571}$. Das Hamming–Gewicht für alle $m = 3$ Zeilen ist $w_{\rm Z} = 4$ und für das mittlere Hamming–Gewicht über alle Spalten gilt:
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] = 12/7 \hspace{0.05cm}.$$
Damit gilt für die angegebene untere Schranke der Coderate:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} = 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$
Das bedeutet: Die tatsächliche Coderate ist gleich der unteren Schranke ⇒ die $m = 3$ Prüfgleichungen von $\mathbf{H}_1$ sind linear unabhängig.
(3) Die erste Zeile von $\mathbf{H}_2$ ist die Summe aus der ersten Zeile $(z_1)$ und der zweiten Zeile $(z_2)$ von $\mathbf{H}_1$. Die zweite Zeile ist gleich $z_2 + z_3$ und die dritte Zeile ist $z_1 + z_3$. Es handelt sich um den identischen Code ⇒ Rate $R = 4/7 = 0.571$. Weiterhin gilt $w_{\rm Z} = 4$ und ${\rm E}[w_{\rm S}] = 1/7 \cdot [0 + 6 \cdot 2] = 12/7$.
(4) Für diesen Code mit $n = 7$ (Spaltenzahl) und $m = 4$ (Zeilenzahl) gilt:
- $$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7$$
- $$\Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$
Das Gleichheitszeichen würde nur bei linear unabhängigen Prüfgleichungen gelten, was hier nicht zutrifft: Die dritte Zeile von $\mathbf{H}_3$ wurde von $\mathbf{H}_1$ übernommen. Streicht man diese Zeile, so ist $\mathbf{H}_3 = \mathbf{H}_2$ und deshalb gilt ebenfalls: $\ \underline{R = 4/7 = 0.571}$.
(5) Hier gilt $n = 7$ und $m = 4$, sowie
- $${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},$$
- $${\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$
- $$\Rightarrow \hspace{0.3cm}R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{23/8}{23/4} = 1/2 \hspace{0.05cm}.$$
Da alle vier Gleichungen linear unabhängig sind, ist die Coderate gleich der unteren Schranke: $\underline{R = 1/2}$. Hinweis: Es handelt sich um den erweiterten (8, 4, 4)–Hamming–Code.