Exercise 4.5: On the Extrinsic L-values again

Ergebnistabelle nach dem ersten $L_{\rm E}(i)$–Ansatz

Wir gehen wie im Theorieteil vom Single Parity–check Code $\rm SPC \, (3, \, 2, \, 2)$ aus. Die möglichen Codeworte sind $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} \{ \underline{x}_0,\hspace{0.05cm} \underline{x}_1,\hspace{0.05cm} \underline{x}_2,\hspace{0.05cm} \underline{x}_3\}$ mit

$$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$

$$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$

$$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$

$$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$

In der Aufgabe verwenden wir meist die zweite (bipolare) Darstellung der Codesymbole: $x_i ∈ \{+1, -1\}$.

Es ist nicht so, dass der $\rm SPC \, (3, \, 2, \, 2)$ von großem praktischen Interesse wäre, da zum Beispiel bei Hard Decision wegen $d_{\rm min} = 2$ nur ein Fehler erkannt und kein einziger korrigiert werden kann. Der Code ist aber wegen des überschaubaren Aufwands für Übungs– und Demonstrationszwecke gut geeignet.
Mit iterativer symbolweiser Decodierung kann man auch einen Fehler korrigieren. Beim vorliegenden Code müssen die extrinsischen $L$–Werte $\underline{L}_{\rm E} = L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)$ entsprechend der folgenden Gleichung berechnet werden.

$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$

Hierbei bezeichnet $\underline{x}^{(-1)}$ alle Symbole mit Ausnahme von $x_i$ und ist somit ein Vektor der Länge $n - 1 = 2$.

Als den ersten $L_{\rm E}(i)$–Ansatz bezeichnen wir die Vorgehensweise entsprechend den Gleichungen

$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$

$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$

$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$

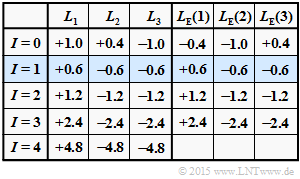
(1) Dieser $L_{\rm E}(i)$–Ansatz liegt der obigen Ergebnistabelle (rote Einträge) zugrunde, wobei von folgenden Aposteriori–$L$–Werten ausgegangen wird:

$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}{\rm kurz\hspace{-0.1cm}:}\hspace{0.25cm} L_1 = +1.0\hspace{0.05cm},\hspace{0.05cm} L_2 = +0.4\hspace{0.05cm},\hspace{0.05cm} L_3 = -1.0\hspace{0.05cm}.$$

(2) Die extrinsischen $L$–Werte für die nullte Iteration ergeben sich zu $L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337$ und $L_{\rm E}(3) = +0.1829$. Diese Werte werden in der Aufgabe 4.5Z berechnet.

(3) Die Aposteriori–Werte zu Beginn der ersten Iteration sind damit

$$\underline{L}^{(I=1)} = \underline{L}^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) \hspace{0.05cm} . $$

(4) Daraus ergeben sich die neuen extrinsischen Werte für die Iterationsschleife $I = 1$ wie folgt:

$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \right ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$

$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \right ] = - 0.3023\hspace{0.05cm}.$$

Weiter erkennt man aus der oberen Tabelle:

Eine harte Entscheidung entsprechend den Vorzeichen vor der ersten Iteration ⇒ Iteration $I = 0$ scheitert, da $(+1, +1, -1)$ kein gültiges $\rm SPC \, (3, \, 2, \, 2)$–Codewort ist.
Schon nach $I = 1$ Iterationen liefert eine harte Entscheidung ein gültiges Codewort, nämlich $\underline{x}_2 = (+1, -1, -1)$. Auch in späteren Grafiken sind die Zeilen erstmals richtige HD–Entscheidungen blau hinterlegt.
Harte Entscheidungen nach weiteren Iterationen $(I ≥ 2)$ führen jeweils zum gleichen Codewort $\underline{x}_2$. Diese Aussage gilt nicht nur für dieses Beispiel, sondern ganz allgemein.

Daneben betrachten wir in dieser Aufgabe einen zweiten $L_{\rm E}(i)$–Ansatz, der hier am Beispiel für das erste Symbol $(i = 1)$ angegeben wird:

$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)]\hspace{0.05cm},\hspace{0.8cm} |L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$

Dieser zweite Ansatz basiert auf der Annahme, dass die Zuverlässigkeit von $L_{\rm E}(i)$ im wesentlichen durch das unzuverlässige Nachbarsymbol bestimmt wird. Das bessere (größere) Eingangs–LLR wird dabei völlig außer Acht gelassen. – Betrachten wir hierzu zwei Beispiele:

(1) Für $L_2 = 1.0$ und $L_3 = 5.0$ ergibt sich beispielsweise

nach dem ersten Ansatz: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \right ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$
nach dem zweiten Ansatz: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \right ) = 1.000 \hspace{0.05cm}.$

(2) Dagegen erhält man für $L_2 = L_3 = 1.0$

nach dem ersten Ansatz: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \right ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$
nach dem zweiten Ansatz: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 1.000 \hspace{0.05cm}.$

Man erkennt die deutliche Diskrepanz zwischen beiden Ansätzen. Der zweite Ansatz (Näherung) ist deutlich positiver als der erste (richtige) Ansatz. Wichtig ist eigentlich aber nur, dass die Iterationen zum gewünschten Decodierergebnis führt.

Hinweise:

Die Aufgabe gehört zum Kapitel Soft–in Soft–Out Decoder.
Bezug genommen wird insbesondere auf die Seite Zur Berechnung der extrinsischen L–Werte.
Behandelt wird hier ausschließlich der zweite Lösungsansatz.
Zum ersten Lösungsansatz verweisen wir auf die Aufgabe 4.5Z .
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

Musterlösung

Solution

(1) Entsprechend dem zweiten $L_{\rm E}(i)$–Ansatz gilt:

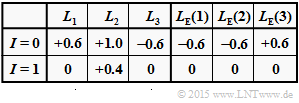
$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$

$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4$$

$$\Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$

$\underline{L}(+1.0, +0.4, –1.0)$–Ergebnistabelle

In gleicher Weise erhält man:

$$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, \hspace{0.3cm} L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$

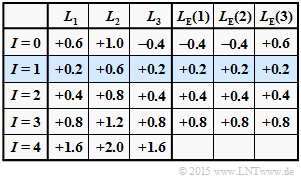
(2) Die Aposteriori–$L$–Werte zu Beginn der ersten Iteration $(I = 1)$ ergeben sich aus der Summe der bisherigen $L$–Werte (für $I = 0$) und den unter (1) berechneten extrinsischen Werten:

$$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$

$$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$

$$L_3 = L_{\rm APP}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (-1.0) + 0.4\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm}.$$

(3) Wie aus obiger Tabelle hervorgeht, sind die Lösungsvorschläge 1 und 2 richtig im Gegensatz zur Antwort 3: Mit jeder neuen Iteration werden die Beträge von $L(1), \ L(2)$ und $L(3)$ signifikant größer.

(4)

$\underline{L}(+0.6, +1.0, –0.4)$–Ergebnistabelle

Wie aus nebenstehender Tabelle hervorgeht, sind die Antworten 1 und 3 richtig. Die Entscheidung fällt also für das Codewort $\underline{x}_0 = (+1, +1, +1)$. Ab $I = 1$ wäre dies auch die Entscheidung von Hard Decision.

$\underline{L}(+0.6, +1.0, –0.8)$–Ergebnistabelle

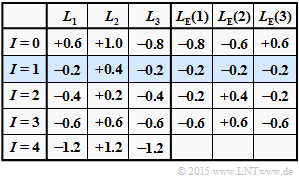
(5) Wegen $|L(3)| > |L(1)|$ gilt bereits ab $I = 1$:

$$L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} L_3 < 0 \hspace{0.05cm}.$$

Ab dieser Iterationsschleife liefert Hard Decision das Codewort $\underline{x}_2 = (-1, +1, -1)$. Richtig sind somit die Antworten 2 und 3.

(6)

$\underline{L}(+0.6, +1.0, –0.6)$–Ergebnistabelle

Die nebenstehende Tabelle zeigt, dass unter der Voraussetzung $|L(1)| = |L(3)|$ ab der Iterationsschleife $I = 1$ alle extrinsischen $L$–Werte $0$ sind. Damit bleiben die Aposteriori–$L$–Werte auch für $I > 1$ konstant gleich $\underline{L} = (0., +0.4, 0.)$, was keinem Codewort zugeordnet werden kann ⇒ Lösungsvorschlag 3.

	Hard Decision nach $I = 1$ führt zum Codewort $\underline{x}_1 = (+1, -1, -1)$.
	Daran ändert sich auch nach weiteren Iterationen nichts.
	Weitere Iterationen erhöhen die Zuverlässigkeit für $\underline{x}_1$ nicht.

	Die iterative Decodierung führt zum Ergebnis $\underline{x}_0 = (+1, +1, +1)$.
	Die iterative Decodierung führt zum Ergebnis $\underline{x}_2 = (-1, +1, -1)$.
	Dieses Ergebnis liefert auch Hard Decision ab $I = 1$.

	Die iterative Decodierung führt zum Ergebnis $\underline{x}_0 = (+1, +1, +1)$.
	Die iterative Decodierung führt zum Ergebnis $\underline{x}_2 = (-1, +1, -1)$.
	Die iterative Decodierung führt nicht zum Ziel.