Exercise 2.10Z: Noise with DSB-AM and SSB-AM
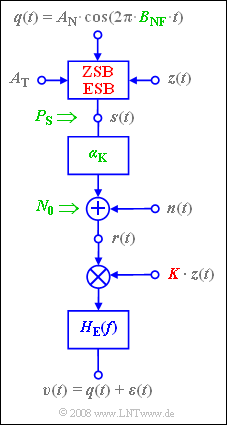
Nun soll der Einfluss von Rauschen auf den Sinken–Störabstand $10 · \lg ρ_v$ bei ZSB– bzw. ESB–AM–Übertragung vergleichend gegenübergestellt werden. Die Grafik zeigt das zugrundeliegende Blockschaltbild.
Rot hervorgehoben sind in diesem Bild die Unterschiede zwischen den beiden Systemvarianten, nämlich der Modulator (ZSB bzw. ESB) sowie die dimensionslose Konstante
- $$ K = \left\{ \begin{array}{c} 2/\alpha_{\rm K} \\ 4/\alpha_{\rm K} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm ESB} \hspace{0.05cm} \\ \end{array}$$
des empfängerseitigen Trägersignals $z_{\rm E}(t) = K · \cos(ω_{\rm T} · t)$, das als frequenz- und phasensynchron mit dem Trägersignal $z(t)$ beim Sender angenommen werden soll.
In grüner Farbe beschriftet sind diejenigen Systemkenngrößen, die in der gemeinsamen Leistungskenngröße
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
zusammengefasst sind. Weiter ist zu beachten:
- Das Cosinussignal $q(t)$ mit der Frequenz $B_{\rm NF}$ steht stellvertretend für ein aus mehreren Frequenzen zusammengesetztes Quellensignal der Bandbreite $B_{\rm NF}$.
- Die ZSB–AM mit Träger wird durch den Modulationsgrad $m = A_{\rm N}/A_{\rm T}$ parametrisiert, während die ESB–AM durch das Seitenband–zu–Träger–Verhältnis $μ = A_{\rm N}/(2 · A_{\rm T})$ bestimmt ist.
- Die frequenzunabhängige Kanaldämpfung $α_{\rm K}$ wird durch die Konstante $K$ ausgeglichen, so dass im rauschfreien Fall ($N_0 = 0$) das Sinkensignal $v(t)$ mit dem Quellensignal $q(t)$ übereinstimmt.
- Das Sinken–SNR kann somit wie folgt angegeben werden ($T_0$ gibt hierbei die Periodendauer des Quellensignals an):
- $$ \rho_{v } = \frac{P_{q}}{P_{\varepsilon }}\hspace{0.5cm}{\rm mit}\hspace{0.5cm} P_{q} = \frac{1}{T_{\rm 0}}\cdot\int_{0}^{ T_{\rm 0}} {q^2(t)}\hspace{0.1cm}{\rm d}t, \hspace{0.5cm}P_{\varepsilon} = \int_{-B_{\rm NF}}^{ +B_{\rm NF}} \hspace{-0.1cm}{\it \Phi_{\varepsilon}}(f)\hspace{0.1cm}{\rm d}f\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einseitenbandmodulation.
- Bezug genommen wird insbesondere auf die Seite Seitenband-zu-Träger-Verhältnis.
- Die Ergebnisse für die ZSB–AM finden Sie auf der Seite Einfluss von Rauschstörungen im Sinken-SNR und Leistungskenngröße.
Fragebogen
Musterlösung
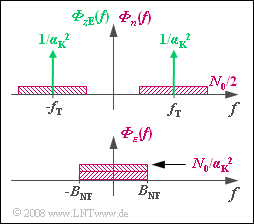
(2) Bei ZSB–AM ohne Träger gilt $P_{\rm S} = P_q/2$. Dies ist auch gleichzeitig die Leistung des Nutzanteils des Sinkensignals $v(t)$. Das Leistungsdichtespektrum ${\it Φ}_ε(f)$ des Rauschanteils von $v(t)$ ergibt sich aus der Faltung:
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{1}{\alpha_{\rm K}^2} \cdot \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
Der Ausdruck [ ... ] beschreibt das Leistungsdichtespektrum eines Cosinussignals mit der Signalamplitude $K = 2$. Mit $1/α_K^2$ wird die Korrektur der Kanaldämpfung berücksichtigt. Unter Berücksichtigung von ${\it \Phi}_n(f) = N_0/2$ ergibt sich somit:
- $${\it \Phi}_\varepsilon(f) = \frac{N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \int_{-B_{\rm NF}}^{+B_{\rm NF}} {{\it \Phi}_\varepsilon(f) }\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
Daraus folgt für das Signal-zu-Rausch-Leistungsverhältnis (SNR):
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}\hspace{0.15cm}\underline { = \xi} \hspace{0.05cm}.$$
Richtig ist also der Lösungsvorschlag 2.
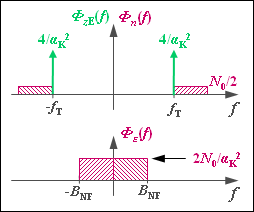
(3) Bei der ESB gilt im Gegensatz zur ZSB $P_S = P_q/4$ sowie
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{4}{\alpha_{\rm K}^2} \cdot \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
Unter Berücksichtigung von $B_{\rm HF} = B_{\rm NF}$ (siehe nebenstehende Skizze für die OSB–Modulation) erhält man nun:
- $${\it \Phi}_\varepsilon(f) = \frac{2 \cdot N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \frac{4 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
Das bedeutet: Verzichtet man auf die Übertragung des Trägers, so zeigt die Einseitenbandmodulation das gleiche Rauschverhalten wie die ZSB–AM ⇒ Lösungsvorschlag 2.
(4) Ausgehend vom cosinusförmigen Träger mit der Amplitude $A_{\rm T}$ und dem ebenfalls cosinusförmigen Nachrichtensignal $q(t)$ erhält man bei ZSB–AM mit Träger:
- $$ s(t) = (q(t) + A_{\rm T}) \cdot \cos( \omega_{\rm T} \cdot t)= = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t) + \frac{A_{\rm N}}{2}\cdot \cos(( \omega_{\rm T}+ \omega_{\rm N}) \cdot t)+ \frac{A_{\rm N}}{2}\cdot \cos(( \omega_{\rm T}- \omega_{\rm N}) \cdot t)\hspace{0.05cm}.$$
Die Sendeleistung ergibt sich somit zu
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + 2 \cdot \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.05cm}.$$
Unter Berücksichtigung von $P_q = A_{\rm N}^2/2$ und $m = A_{\rm N}/A_{\rm T}$ kann hierfür auch geschrieben werden:
- $$P_{\rm S}= \frac{A_{\rm N}^2}{4} \cdot \left[ 1 + \frac{2 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{2} \cdot \left[ 1 + {2 }/{m^2}\right]\hspace{0.05cm}.$$
Mit der Rauschleistung $P_ε$ gemäß Teilaufgabe (2) erhält man somit:
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}\cdot (1 + 2/m^2)}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{2 }/{m^2}} \hspace{0.05cm},$$
und in logarithmischer Darstellung:
- $$ 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{2 }/{m^2}}\right] \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 0.5) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (9) \hspace{0.15cm}\underline {= 30.46\, {\rm dB}}$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 1.0) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (3) \hspace{0.15cm}\underline {= 35.23\, {\rm dB} \hspace{0.05cm}}.$$
(5) Bei der ESB–AM gibt es nur ein Seitenband und es gilt unter Berücksichtigung des Seitenband–zu–Träger–Verhältnisses $μ = A_{\rm N}/(2A_{\rm T})$:
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm N}^2}{8} \cdot \left[ 1 + \frac{4 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{4} \cdot \left[ 1 + {1 }/{\mu^2}\right] \hspace{0.05cm}.$$
Somit erhält man mit der Rauschleistung entsprechend der Teilaufgabe (3):
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{4 \cdot P_{\rm S}\cdot (1 + 1/\mu^2)}{4 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{1 }/{\mu^2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{1 }/{\mu^2}}\right] \hspace{0.05cm}.$$
Das bedeutet: Man erhält bei der ESB–AM das gleiche Ergebnis wie bei einer ZSB–AM mit dem Modulationsgrad $m = \sqrt{2} · μ$. Daraus folgt weiter:
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ESB,} \hspace{0.1cm}\mu = {0.5}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ZSB,} \hspace{0.1cm}m=0.5) \hspace{0.15cm}\underline {=30.46\,{\rm dB}},$$
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ESB,} \hspace{0.1cm}\mu = {1.0}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ZSB,} \hspace{0.1cm}m=1.0) \hspace{0.15cm}\underline {=35.23\,{\rm dB}}\hspace{0.05cm}.$$