Exercise 2.5: DSB-AM via a Gaussian channel
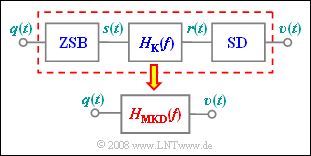
Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen:
- ZSB–AM ohne Träger mit $f_{\rm T} = 50 \ \rm kHz$ bzw. $f_{\rm T} = 55 \ \rm kHz$:
- $$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$
- Gaußförmiger Bandpass–Kanalfrequenzgang (der Betrag $|f|$ im Exponenten berücksichtigt, dass $H_K(–f) = H_K(f)$ gilt):
- $$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{|f| - f_{\rm M}}{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$
- Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $v(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_{\rm K}(f) = 1$ ist.
Auf der Seite Einfluss linearer Kanalverzerrungen wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right]$$
ausreichend genau charakterisiert ist. Der Index steht hierbei für „Modulator–Kanal–Demodulator”.
Das Quellensignal $q(t)$ setzt sich aus zwei Cosinus-Schwingungen zusammen:
- $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seite Einfluss linearer Kanalverzerrungen.
Fragebogen
Musterlösung
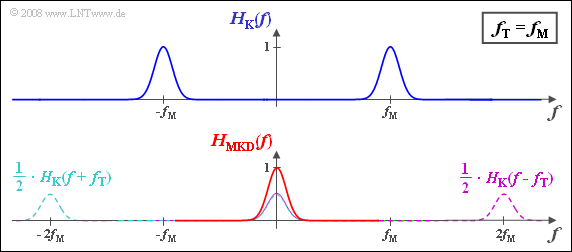
Bei niedrigen Frequenzen ergibt sich dann eine Gaußfunktion um die Mittenfrequenz „0”:
- $$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$
Die beiden Anteile bei $±2f_{\rm T}$ müssen nicht weiter betrachtet werden. Für die zwei gesuchten Frequenzen $f_1 = 1\ \rm kHz$ und $f_5 = 5 \ \rm kHz$ erhält man:
- $$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$
- $$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$
(2) Mit $ω_1 = 2π · 1\ \rm kHz$ und $ω_5 = 2π · 5 \ \rm kHz$ gilt:
- $$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$
Man erkennt, dass nun – im Gegensatz zum Quellensignal $q(t)$ – der Anteil bei $1 \ \rm kHz$ ⇒ $A_1 = 1.938 \ \rm V$ größer ist als der $5 \ \rm kHz$–Anteil ⇒ $A_5 = 1.368 \ \rm V$, da der Kanal die Frequenzen $49 \ \rm kHz$ und $51 \ \rm kHz$ weniger dämpft als die Spektralanteile bei $45 \ \rm kHz$ und $55 \ \rm kHz$.
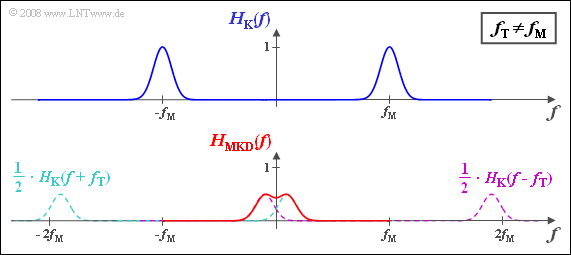
(3) Die beiden um $±f_{\rm T}$ verschobenen Spektralfunktionen kommen nun nicht mehr direkt übereinander zu liegen, sondern sind um $10 \ \rm kHz$ gegeneinander versetzt. Der resultierende Frequenzgang $H_{\rm MKD}(f)$ ist somit nicht mehr gaußförmig, sondern es gilt entsprechend der unteren Skizze:
- $$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$
Für die Frequenzen $f_1$ und $f_5$ erhält man:
- $$H_{\rm MKD}(f = 1\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 56\,{\rm kHz}) + H_{\rm K}(f = -54\,{\rm kHz})\right]=$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{56\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-54\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.161 + 0.302 \hspace{0.15cm}\underline {= 0.463}\hspace{0.05cm},$$
- $$H_{\rm MKD}(f = 5\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 60\,{\rm kHz}) + H_{\rm K}(f = -50\,{\rm kHz})\right]= \hspace{0.75cm}$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$
Während bei $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ der Synchrondemodulator die Information über das Nachrichtensignal aus beiden Seitenbändern in gleicher Weise gewinnt, liefert mit $f_{\rm T} = 55\ \rm kHz$ das untere Seitenband (USB) den größeren Beitrag. Zum Beispiel liegt das USB des $5 \ \rm kHz$–Anteils nun genau bei $f_{\rm M} = 50 \ \rm kHz$ und wird ungedämpft übertragen, während das OSB bei $60 \ \rm kHz$ starken Dämpfungen unterliegt.
(4) Mit dem Ergebnis der letzten Teilaufgabe erhält man:
- $$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$
- $$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$
In diesem Fall sind die linearen Verzerrungen sogar weniger stark, da auch der $1 \ \rm kHz$–Anteil stärker gedämpft wird.
(5) Richtig ist JA:
- Mit der Trägerfrequenz $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ wird der $5 \ \rm kHz$–Anteil stärker gedämpft als der $1 \ \rm kHz$–Anteil, während mit $f_{\rm T} = 55 \ \rm kHz \ne f_{\rm M}$ der $1 \ \rm kHz$–Anteil etwas mehr gedämpft wird.
- Wählt man nun zum Beispiel $f_{\rm T} \approx 54.5 \ \rm kHz$, so werden beide Anteile gleich gedämpft (etwa um den Faktor $0.53$) und es gibt keine Verzerrungen.
- Dieses Ergebnis gilt allerdings nur für das betrachtete Quellensignal. Ein anderes $q(t)$ mit ebenfalls zwei Spektralanteilen würde eine andere „optimale Trägerfrequenz” erfordern.
- Bei einem Nachrichtensignal mit drei oder mehr Spektrallinien würde es stets zu linearen Verzerrungen kommen.