Bessel functions of the first kind

Programmbeschreibung

Dieses Applet ermöglicht die Berechnung und graphische Darstellung der Besselfunktionen erster Art und $n$–ter Ordnung entsprechend der Reihendarstellung:

$${\rm J}_n (x) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (x/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$

Graphisch dargestellt werden die Funktionen ${\rm J}_n (x)$ für die Ordnung $n=0$ bis $n=9$ in verschiedenen Farben.
Die Numerikausgabe liefert die Funtionswerte ${\rm J}_0 (x)$ ... ${\rm J}_9 (x)$ für einen per Slider einstellbaren Wert $x$ im Bereich $0 \le x \le 15$ mit Schrittweite $0.5$.

Theoretischer Hintergrund

Allgemeines zu den Besselfunktionen

Besselfunktionen (oder auch Zylinderfunktionen) sind Lösungen der Besselschen Differentialgleichung der Form

$$x^2 \cdot \frac{ {\rm d}^2}{{\rm d}x^2}{\rm J}_n (x) \ + \ x \cdot \frac{ {\rm d}}{{\rm d}x}{\rm J}_n (x) \ + \ (x^2 - n^2) \cdot {\rm J}_n (x)= 0. $$

Hierbei handelt es sich um eine gewöhnliche lineare Differentialgleichung zweiter Ordnung. Der Parameter $n$ ist meistens eine ganze Zahl, so auch in diesem Programm. Diese bereits 1844 von Friedrich Wilhelm Bessel eingeführten mathematischen Funktionen können auch in geschlossener Form als Integrale dargestellt werden:

$${\rm J}_n (x) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}[\hspace{0.05cm}x \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha \hspace{0.05cm}]}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$

Sie spielen eine wichtige Rolle in der Physik. Man trifft u.a. bei der Untersuchung von Eigenschwingungen von zylindrischen Resonatoren, der Analyse des Frequenzspektrums von frequenzmodulierten Signalen und dem Sättigungsverhalten von Klystrons auf die Besselfunktionen. Man zählt die Besselfunktionen wegen ihrer vielfältigen Anwendungen in der mathematischen Physik zu den speziellen Funktionen. Die Funktionswerte entnimmt man in der Praxis aus Bessel-Funktionstabellen. ${\rm Q}(x)$ und $1/2\cdot {\rm erfc}(x)$, die für die Fehlerwahrscheinlichkeitsberechnung von großer Bedeutung sind.

Sowohl die Abszisse als auch der Funktionswert kann entweder linear oder logarithmisch dargestellt werden.
Für beide Funktionen wird jeweils eine obere Schranke (englisch: Upper Bound ) und eine untere Schranke (englisch: Lower Bound) angegeben.

Diese bereits 1844 von Friedrich Wilhelm Bessel eingeführten mathematischen Funktionen sind wie folgt definiert (erste Gleichung) und können gemäß der zweiten Gleichung durch eine Reihe angenähert werden:

Zur Berechnung der Besselfunktionen

Die nebenstehende Grafik zeigt die jeweils ersten drei Summanden $(k = 0, 1, 2)$ der Reihen ${\rm J}_0(η)$, ... , ${\rm J}_3(η).$ Der rot umrandete Term – gültig für $n = 3$ und $k = 2$ – lautet beispielsweise in ausgeschriebener Form:

$$\frac{(-1)^2 \cdot (\eta/2)^{3 \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}2}}{2\hspace{0.05cm}! \cdot (3+2)\hspace{0.05cm}!} = \frac{1}{240}\cdot (\frac{\eta}{2})^7 \hspace{0.05cm}.$$

Die Besselfunktionen $J_n(η)$ findet man aber auch in Formelsammlungen oder mit Hilfe des von uns bereitgestellten Berechnungsmodul Besselfunktion erster Art und $n$–ter Ordnung.
Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden:

$${\rm J}_n (\eta) ={2 \cdot (n-1)}/{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$

Bei der Untersuchung digitaler Übertragungssysteme muss oft die Wahrscheinlichkeit bestimmt werden, dass eine (mittelwertfreie) gaußverteilte Zufallsgröße $x$ mit der Varianz $σ^2$ einen vorgegebenen Wert $x_0$ überschreitet. Für diese Wahrscheinlichkeit gilt:

$${\rm Pr}(x > x_0)={\rm Q}(\frac{x_0}{\sigma}) = 1/2 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$

Die Funktion ${\rm Q}(x )$

Die Funktion ${\rm Q}(x)$ bezeichnet man als das Komplementäre Gaußsche Fehlerintegral. Es gilt folgende Berechnungsvorschrift:

$${\rm Q}(x ) = \frac{1}{\sqrt{2\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}/\hspace{0.05cm} 2}\,{\rm d} u .$$

Dieses Integral ist nicht analytisch lösbar und muss – wenn man dieses Applet nicht zur Verfügung hat – aus Tabellen entnommen werden.
Speziell für größere $x$–Werte von (also für kleine Fehlerwahrscheinlichkeiten) liefern die nachfolgend angegebenen Schranken eine brauchbare Abschätzung für das Komplementäre Gaußsche Fehlerintegral, die auch ohne Tabellen berechnet werden können.
Eine obere Schranke (englisch: Upper Bound ) des Komplementären Gaußschen Fehlerintegrals lautet:

$${\rm Q}_{\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ] = \frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x).$$

Entsprechend gilt für die untere Schranke (englisch: Lower Bound ):

$${\rm Q}_{\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ] =\frac{1-1/x^2}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{-x^ 2/\hspace{0.05cm}2} ={\rm Q}_{\rm UB}(x ) \cdot (1-1/x^2)< {\rm Q}(x).$$

In vielen Programmbibliotheken findet man allerdings die Funktion ${\rm Q}(x )$ nicht.

Die Funktion $1/2 \cdot {\rm erfc}(x )$

In fast allen Programmbibliotheken findet man dagegen die Komplementäre Gaußsche Fehlerintegral (englisch: Complementary Gaussian Error Function)

$${\rm erfc}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$

die mit ${\rm Q}(x)$ wie folgt zusammenhängt: ${\rm Q}(x)=1/2\cdot {\rm erfc}(x/{\sqrt{2}}).$ Da bei fast allen Anwendungen diese Funktion mit dem Faktor $1/2$ verwendet wird, wurde in diesem Applet genau diese Funktion realisiert:

$$1/2 \cdot{\rm erfc}(x) = \frac{1}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$

Auch für diese Funktion kann wieder eine obere und eine untere Schranke angegeben werden:

$$\text{Upper Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ 1}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} ,$$

$$\text{Lower Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ {1-1/(2x^2)}}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} .$$

Wann bietet welche Funktion Vorteile?

$\text{Beispiel 1:}$ Wir betrachten die binäre Basisbandübertragung. Hier lautet die Bitfehlerwahrscheinlichkeit $p_{\rm B} = {\rm Q}({s_0}/{\sigma_d})$, wobei das Nutzsignal die Werte $\pm s_0$ annehmen kann und der Rauscheffektivwert $\sigma_d$ ist.

Es wird vorausgesetzt, dass Tabellen zur Verfügung stehen, in denen das Argument der Gaußschen Fehlerfunktionen im Abstand $0.1$ aufgelistet sind. Mit $s_0/\sigma_d = 4$ erhält man für die Bitfehlerwahrscheinlichkeit gemäß der Q–Funktion:

$$p_{\rm B} = {\rm Q} (4) \approx 0.317 \cdot 10^{-4}\hspace{0.05cm}.$$

Nach der zweiten Gleichung ergibt sich:

$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2} })= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.$$

Richtiger ist der erste Wert. Bei der zweiten Berechnungsart muss man runden oder – noch besser – interpolieren, was aufgrund der starken Nichtlinearität dieser Funktion sehr schwierig ist.
Bei den gegebenen Zahlenwerten ist demnach Q–Funktion besser geeignet. Außerhalb von Übungsbeispielen wird $s_0/\sigma_d$ in der Regel einen „krummen” Wert besitzen. In diesem Fall bietet ${\rm Q}(x)$ natürlich keinen Vorteil gegenüber $1/2 \cdot{\rm erfc}(x)$.

$\text{Beispiel 2:}$ Mit der Energie pro Bit $(E_{\rm B})$ und der Rauschleistungsdichte $(N_0)$ gilt für die Bitfehlerwahrscheinlichkeit von Binary Phase Shift Keying (BPSK):

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2 E_{\rm B} }/{N_0} }\right ) = {1}/{2} \cdot {\rm erfc} \left ( \sqrt{ {E_{\rm B} }/{N_0} }\right ) \hspace{0.05cm}.$$

Für die Zahlenwerte $E_{\rm B} = 16 \ \rm mWs$ und $N_0 = 16 \ \rm mW/Hz$ erhält man:

$$p_{\rm B} = {\rm Q} \left (4 \cdot \sqrt{ 2} \right ) = {1}/{2} \cdot {\rm erfc} \left ( 4\right ) \hspace{0.05cm}.$$

Der erste Weg führt zum Ergebnis $p_{\rm B} = {\rm Q} (5.657) \approx {\rm Q} (5.7) = 0.6 \cdot 10^{-8}\hspace{0.05cm}$, während $1/2 \cdot{\rm erfc}(x)$ hier den richtigeren Wert $p_{\rm B} \approx 0.771 \cdot 10^{-8}$ liefert.
Wie im ersten Beispiel erkennt man aber auch hier: Die Funktionen ${\rm Q}(x)$ und $1/2 \cdot{\rm erfc}(x)$ sind grundsätzlich gleich gut geeignet. Vor– oder Nachteile der einen oder anderen Funktion ergeben sich nur bei konkreten Zahlenwerten.

Zur Handhabung des Applets

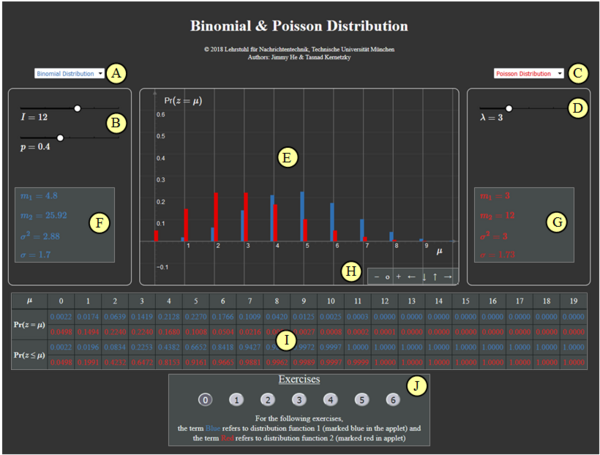
(A) Vorauswahl für blauen Parametersatz

(B) Parametereingabe $I$ und $p$ per Slider

(C) Vorauswahl für roten Parametersatz

(D) Parametereingabe $\lambda$ per Slider

(E) Graphische Darstellung der Verteilungen

(F) Momentenausgabe für blauen Parametersatz

(G) Momentenausgabe für roten Parametersatz

(H) Variation der grafischen Darstellung

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$

(J) Bereich für die Versuchsdurchführung

Andere Möglichkeiten zur Variation der grafischen Darstellung:

Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2007 von Thomas Großer im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2018 wurde das Programm von Marwen ??? (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab