Exercise 2.3Z: Asymmetrical Characteristic Operation

• Return to book

Einfluss nichtlinearer Verzerrungen

Am Eingang eines Systems $S$ liegt das Cosinussignal

$$x(t) = A \cdot \cos(\omega_0 t)$$

an, wobei für die Amplitude stets $A = 0.5$ gelten soll. Das System $S$ besteht

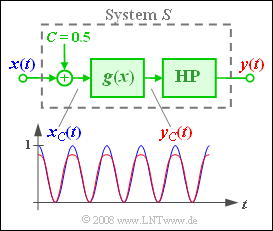
• aus der Addition eines Gleichanteils $C$,
• einer Nichtlinearität mit der Kennlinie

$$g(x) = \sin(x) \hspace{0.05cm} \approx x -{x^3}\hspace{-0.1cm}/{6} = g_3(x),$$

• sowie einem idealen Hochpass, der alle Frequenzen bis auf ein Gleichsignal $(f = 0)$ unverfälscht passieren lässt.

Das Ausgangssignal des Gesamtsystems kann allgemein wie folgt dargestellt werden:

$$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm}\text{...}$$

Die sinusförmige Kennlinie $g(x)$ soll in der gesamten Aufgabe entsprechend der obigen Gleichung durch die kubische Näherung  $g_3(x)$  approximiert werden. Für $C = 0$ ergäbe sich somit die exakt gleiche Konstellation wie in Aufgabe 2.3, in deren Unterpunkt (2) der Klirrfaktor berechnet wurde:

• $K = K_{g3} \approx 1.08 \%$  für  $A = 0.5$,
• $K = K_{g3} \approx 4.76 \%$  für  $A = 1.0$.

Unter Berücksichtigung der Konstanten $A = C = 0.5$ gilt für das Eingangssignal der Nichtlinearität:

$$x_{\rm C}(t) = C + A \cdot \cos(\omega_0 t) = {1}/{2} + {1}/{2}\cdot \cos(\omega_0 t).$$

• Die Kennlinie wird also unsymmetrisch betrieben mit Werten zwischen $0$ und $1$.
• In obiger Grafik sind zusätzlich die Signale $x_{\rm C}(t)$ und $y_{\rm C}(t)$ direkt vor und nach der Kennlinie $g(x)$ eingezeichnet.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel  Nichtlineare Verzerrungen.

• Als bekannt vorausgesetzt werden die folgenden trigonometrischen Beziehungen:

$$\cos^2(\alpha) = {1}/{2} + {1}/{2} \cdot \cos(2\alpha)\hspace{0.05cm}, \hspace{0.3cm} \cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie das Ausgangssignal $y(t)$ unter Berücksichtigung des Hochpasses. Wie lautet der Gleichsignalanteil $A_0$?

$A_0 \ = \ $

2

Geben Sie die weiteren Fourierkoeffizienten des Signals $y(t)$ an.

$A_1 \ = \ $

$A_2 \ = \ $

$A_3 \ = \ $

$A_4 \ = \ $

3

Berechnen Sie den Klirrfaktor des Gesamtsystems.

$K \ = \ $ $\ \%$

4

Berechnen Sie den Maximal– und den Minimalwert des Signals $y(t)$.

$y_\text{max} \ = \ $

$y_\text{min} \ = \ $

Musterlösung

Solution

(1)  Unter Berücksichtigung der kubischen Näherung $g_3(x)$ erhält man vor dem Hochpass:

$$y_{\rm C}(t) = g_3\left[x_{\rm C}(t)\right] = \left[ C + A \cdot \cos(\omega_0 t)\right] - {1}/{6} \cdot \left[ C + A \cdot \cos(\omega_0 t)\right]^3$$

$$\Rightarrow \; y_{\rm C}(t) = C + A \cdot \cos(\omega_0 t) - {1}/{6} \cdot [ C^3 + 3 \cdot C^2 \cdot A \cdot \cos(\omega_0 t) + \hspace{0.09cm}3 \cdot C \cdot A^2 \cdot \cos^2(\omega_0 t) + A^3 \cdot \cos^3(\omega_0 t)].$$

Das Signal $y_{\rm C}(t)$ beinhaltet eine Gleichkomponente $C- C^3/6$, die aufgrund des Hochpasses im Signal $y(t)$ nicht mehr enthalten ist:   $\underline{ A_0 = 0}$.

(2)  Bei Anwendung der angegebenen trigonometrischen Beziehungen erhält man folgende Koeffizienten mit $A= C = 0.5$:

$$A_1 = A - {1}/{6}\cdot 3 \cdot C^2 \cdot A - {1}/{6} cdot {3}/{4}\cdot A^3 = {1}/{2} - {1}/{16} - {1}/{64} = {27}/{64} \hspace{0.15cm}\underline{ \approx 0.422},$$

$$A_2 = - {1}/{6}\cdot 3 \cdot {1}/{2}\cdot C \cdot A^2 = - \frac{1}{32} \hspace{0.15cm}\underline{\approx -0.031},$$

$$A_3 = - {1}/{6}\cdot \frac{1}{4}\cdot A^3 = - {1}/{192} \hspace{0.15cm}\underline{\approx -0.005}.$$

Terme höherer Ordnung kommen nicht vor. Somit ist auch $\underline{A_4 = 0}$.

(3)  Die Klirrfaktoren zweiter und dritter Ordnung ergeben sich bei dieser Aufgabe zu $K_2 = 2/27 \approx 7.41\%$ und $K_3 = 1/81 \approx 1.23\%$ Damit ist der Gesamtklirrfaktor

$$K = \sqrt{K_2^2 + K_3^2} \hspace{0.15cm}\underline{\approx7.51 \%}.$$

(4)  Der Maximalwert tritt zum Zeitpunkt $t = 0$ und bei Vielfachen von $T$ auf:

$$y_{\rm max}= y(t=0) = A_1 + A_2 + A_3 = 0.422 -0.031 -0.005 \hspace{0.15cm}\underline{= 0.386}.$$

Die Minimalwerte liegen genau in der Mitte zwischen den Maxima und es gilt:

$$y_{\rm min}= - A_1 + A_2 - A_3 = -0.422 -0.031 +0.005\hspace{0.15cm}\underline{ = -0.448}.$$

Das Signal $y(t)$ ist gegenüber dem in der Skizze auf der Angabenseite eingezeichnetem Signal um $0.448$ nach unten verschoben. Dieser Signalwert ergibt sich aus folgender Gleichung mit $A = C = 1/2$:

$$C - \frac{C \cdot A^2}{4}- \frac{C^3}{6} = {1}/{2} - {1}/{32}- {1}/{48} = 0.448.$$