Exercise 4.15Z: MSK Basic Pulse and MSK Spectrum

• Return to book

MSK–Grundimpuls und –Spektrum

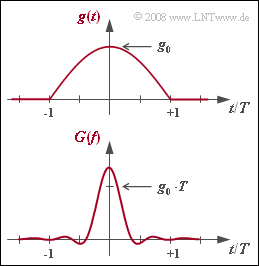
Der zur Realisierung der  MSK mittels Offset–QPSK  stets erforderliche Grundimpuls hat die in der Grafik oben dargestellte Form:

$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$

Darunter gezeichnet ist die Spektralfunktion  $G(f)$, also die  Fouriertransformierte  von  $g(t)$. Die dazugehörige Gleichung soll in dieser Aufgabe ermittelt werden, wobei zu berücksichtigen ist:

$$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$

Hierbei sind folgende Abkürzungen verweendet:

• $c(t)$  ist eine Cosinusschwingung mit Amplitude  $1$  und (noch zu bestimmender) Frequenz  $f_0$.
• $r(t)$  ist eine Rechteckfunktion mit der Amplitude  $g_0$  und der Dauer  $2T$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Nichtlineare digitale Modulation.
• Bezug genommen wird insbesondere auf den Abschnitt  Realisierung der MSK als Offset-QPSK.

• Das hier gewonnene Ergebnis wird auch in der  Aufgabe 4.15  verwendet.

Fragebogen

1

Wie ist die Frequenz  $f_0$  der Cosinusschwingung  $c(t)$  zu wählen, damit  $g(t) = c(t) · r(t)$  gilt?

$f_0 \ = \ $ $\ \cdot 1/T$

2

Wie lautet das Spektrum  $R(f)$  der Rechteckfunktion  $r(t)$? Welcher Spektralwert tritt bei  $f = 0$  auf?

$R(f=0) \ = \ $ $\ \cdot g_0 \cdot T$

3

Berechnen Sie das Spektrum  $G(f)$  des MSK–Impuses  $g(t)$, insbesondere den Spektralwert bei  $f = 0$.

$G(f=0) \ = \ $ $\ \cdot g_0 \cdot T$

4

Fassen Sie das Ergebnis der Teilaufgabe (3) in einem Term zusammen. Bei welcher Frequenz  $f_1$  besitzt  $G(f)$  seine erste Nullstelle?

$f_1 \ = \ $ $\ \cdot 1/T$

Musterlösung

Solution

(1)  Die Periodendauer des Cosinussignals muss $T_0 = 4T$ sein. Damit ist die Frequenz $f_0 = 1/T_0\hspace{0.15cm}\underline {= 0.25} · 1/T$.

(2)  Die Spektralfunktion eines Rechteckimpulses der Höhe $g_0$ und der Dauer 2T lautet:

$$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} \Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$

(3)  Aus $g(t) = c(t) · r(t)$ folgt nach dem Faltungssatz:   $G(f) = C(f) \star R(f)\hspace{0.05cm}.$ Die Spektralfunktion $C(f)$ besteht aus zwei Diracfunktionen bei $± f_0$, jeweils mit dem Gewicht $1/2$. Daraus folgt:

$$G(f) = 2 \cdot g_0 \cdot T \cdot \left [ \frac {1}{2} \cdot \delta (f - f_0 ) + \frac {1}{2} \cdot \delta (f + f_0 )\right ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \left [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \right ] \hspace{0.05cm}.$$

Mit dem Ergebnis $f_0 = 1/(4T)$ der Teilaufgabe (1) gilt weiter:

$$G(f) = g_0 \cdot T \cdot \left [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \right ]$$

$$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \left [ {\rm si} ( - \frac{\pi}{2} ) + {\rm si} ( +\frac{\pi}{2} ) \right ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \frac{\pi}{2} ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$

(4)  Schreibt man die si–Funktion aus, so erhält man mit $\sin (α ± π/2) = ± \cos(α)$:

$$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$

$$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$

• Die Nullstellen von $G(f)$ werden allein durch die Cosinusfunktion im Zähler bestimmt und würden bei den Frequenzen $f · T = 0.25, 0.75, 1.25,$ ... liegen.
• Allerdings wird die erste Nullstelle bei $f · T = 0.25$ durch die gleichzeitige Nullstelle des Nenners aufgehoben. Deshalb gilt:

$$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$