Exercise 2.8: Code Comparison: Binary, AMI and 4B3T

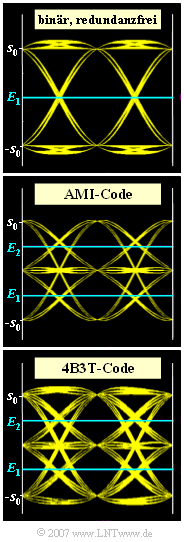
Augendiagramme von verschiedenen Codes

In der Grafik sind drei Augendiagramme (ohne Rauschen) dargestellt, wobei jeweils ein rechteckförmiger NRZ–Sendegrundimpuls und für das Gesamtsystem eine Cosinus–Rolloff–Charakteristik mit Rolloff–Faktor $r = 0.8$ zugrunde liegen. Für die einzelnen Augendiagramme ist weiterhin vorausgesetzt (von oben nach unten):

der redundanzfreie Binärcode,
der AMI–Code (ca. $37 \%$ Redundanz),
der 4B3T–Code (ca. $16 \%$ Redundanz).

Weiter kann von folgenden Voraussetzungen ausgegangen werden:

Es liegt AWGN–Rauschen vor, wobei gilt:

$$10 \cdot {\rm lg}\hspace{0.1cm} ({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB}\hspace{0.05cm}.$$

Die Detektionsstörleistung hat beim Binärsystem folgenden Wert (wegen des nicht optimalen Empfangsfilters $12 \%$–Aufschlag):

$$\sigma_d^2 = 1.12 \cdot {N_0}/({2 T})\hspace{0.05cm}.$$

Die Symbolfehlerwahrscheinlichkeit des Binärsystems lautet:

$$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right) \hspace{0.05cm}.$$

Dagegen gilt für die beiden redundanten Ternärsysteme:

$$p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( s_0/(2 \sigma_d) \right) \hspace{0.05cm}.$$

Zu berücksichtigen ist, dass sich der Rauscheffektivwert $\sigma_{d}$ gegenüber dem redundanzfreien Binärsystem durchaus verändern kann.

Hinweise:

Die Aufgabe gehört zum Kapitel Symbolweise Codierung mit Pseudoternärcodes.
Bezug genommen wird auch auf das Kapitel Blockweise Codierung mit 4B3T-Codes.

Zur numerischen Auswertung der Q–Funktion können Sie das interaktve Applet Komplementäre Gaußsche Fehlerfunktionen verwenden.

Fragebogen

$\sigma_{d}/s_{0} \ = \ $

$\ p_{\rm S} \ = \ $

$\ \cdot 10^{-5}$

$\sigma_{d}/s_{0} \ = \ $

$\ p_{\rm S} \ = \ $

$\ \%$

$\sigma_{d}/s_{0} \ = \ $

$\ p_{\rm S} \ = \ $

$\ \%$

Musterlösung

Solution

(1) Aus dem angegebenen S/N-Verhältnis erhält man:

$$10 \cdot {\rm lg}\hspace{0.1cm}{s_0^2 \cdot T}/{N_0} = 10\, {\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{N_0} = { s_0^2 \cdot T}/{10}$$

$$ \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma_d^2 = 1.12 \cdot {N_0}/({2 T}) = 0.056 \cdot s_0^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{ \sigma_d}/{s_0} \hspace{0.15cm}\underline { = 0.237}\hspace{0.05cm}.$$

(2) Daraus folgt für die Symbolfehlerwahrscheinlichkeit des binären redundanzfreien Referenzsystems:

$$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right)\approx {\rm Q}(4.22)\hspace{0.15cm}\underline { = 1.22 \cdot 10^{-5}} \hspace{0.05cm}.$$

(3) Die Symboldauer $T$ des AMI–codierten Signals ist gleich der Bitdauer $T_{\rm B}$ des Binärsignals. Deshalb ändert sich an den Bandbreitenverhältnissen nichts und man erhält den gleichen Rauscheffektivwert wie unter Punkt (1) berechnet:

$${ \sigma_d}/{s_0}\hspace{0.15cm}\underline { = 0.237} \hspace{0.05cm}.$$

(4) Aufgrund der ternären Entscheidung wird das Argument der Q–Funktion halbiert:

$$p_{\rm S} \approx{4}/{3}\cdot {\rm Q}(2.11)={4}/{3} \cdot 1.74 \cdot 10^{-2}\hspace{0.15cm}\underline { = 2.32 \cdot 10^{-2}} \hspace{0.05cm}.$$

Der Faktor $4/3$ berücksichtigt hierbei, dass das innere Symbol „$0$” nach zwei Richtungen hin verfälscht werden kann.

(5) Bei Anwendung einer 4B3T–Codierung wird die Symbolrate um $25 \%$ verringert. Um den gleichen Faktor $0.75$ wird dadurch die Rauschleistung kleiner als unter (1) und (3) berechnet. Daraus folgt:

$${ \sigma_d}/{s_0} = \sqrt{0.75} \cdot 0.237 \hspace{0.15cm}\underline {\approx 0.205} \hspace{0.05cm}.$$

(6) Aufgrund des kleineren Rauscheffektivwertes ergibt sich nun eine kleinere Fehlerwahrscheinlichkeit als mit dem AMI–Code:

$$p_{\rm S} \approx {4}/{3} \cdot {\rm Q} \left( \frac{0.5}{ 0.205} \right) = {4}/{3} \cdot 0.833 \cdot 10^{-2}\hspace{0.15cm}\underline { = 1.11 \cdot 10^{-2}} \hspace{0.05cm}.$$

Die deutlich kleinere Fehlerwahrscheinlichkeit des redundanzfreien Binärcodes kann der 4B3T–Code aufgrund der ternären Entscheidung (halbe Augenöffnung) jedoch nicht erreichen.