PDF, CDF and Moments of Special Distributions

Open Applet in a new tab

Programmbeschreibung

Das Applet stellt die Beschreibungsformen zweier wertkoninuierlicher Zufallsgrößen  $X$  und  $Y\hspace{-0.1cm}$  vergleichend gegenüber, wobei für die rote Zufallsgröße  $X$  und die blaue Zufallsgröße  $Y$  jeweils folgende Grundformen zur Auswahl stehen:

• Gaußverteilung, Gleichverteilung, Dreieckverteilung, Exponentialverteilung, Laplaceverteilung, Rayleighverteilung, Riceverteilung, Weibullverteilung, Wigner–Halbkreisverteilung, Wigner–Parabelverteilung, Cauchyverteilung.

Die folgenden Angaben beziehen sich auf die Zufallsgrößen  $X$. Graphisch dargestellt werden

• die Wahrscheinlichkeitsdichtefunktion  $f_{X}(x)$  (oben) und
• die Verteilungsfunktion  $F_{X}(x)$  (unten).

Zusätzlich werden noch einige integrale Kenngrößen ausgegeben, nämlich

• der lineare Mittelwert  $m_X = {\rm E}\big[X \big]$,
• der quadratische Mittelwert  $P_X ={\rm E}\big[X^2 \big]$,
• die Varianz  $\sigma_X^2 = P_X - m_X^2$,
• die Standardabweichung (oder Streuung)  $\sigma_X$,
• die Charliersche Schiefe  $S_X$,
• die Kurtosis  $K_X$.

Definition und Eigenschaften der dargestellten Beschreibungsgrößen

In diesem Applet betrachten wir ausschließlich (wert–)kontinuierliche Zufallsgrößen, also solche, deren mögliche Zahlenwerte nicht abzählbar sind.

• Der Wertebereich dieser Zufallsgrößen ist somit im allgemeinen der der reellen Zahlen  $(-\infty \le X \le +\infty)$.
• Es ist aber möglich, dass der Wertebereich auf ein Intervall begrenzt ist:  $x_{\rm min} \le X \le +x_{\rm max}$.

Wahrscheinlichkeitsdichtefunktion (WDF)

Bei einer kontinuierlichen Zufallsgröße  $X$  sind die Wahrscheinlichkeiten, dass  $X$  ganz bestimmte Werte  $x$  annimmt, identisch Null:  ${\rm Pr}(X= x) \equiv 0$.  Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die  Wahrscheinlichkeitsdichtefunktion  – abgekürzt  $\rm WDF$  – übergegangen werden.

$\text{Definition:}$  Der Wert der  Wahrscheinlichkeitsdichtefunktion  $f_{X}(x)$  an der Stelle  $x$  ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße  $X$  in einem (unendlich kleinen) Intervall der Breite  $Δx$  um  $x$  liegt, dividiert durch  $Δx$:

$$f_X(x) = \lim_{ {\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0} \frac{ {\rm Pr} \big [x - {\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/2 \big ] }{ {\rm \Delta} x}.$$

Die englische Bezeichnung für die Wahrscheinlichkeitsdichtefunktion (WDF) ist  Probability Density Function  (PDF).

Die WDF weist folgende Eigenschaften auf:

• Für die Wahrscheinlichkeit, dass die Zufallsgröße  $X$  im Bereich zwischen  $x_{\rm u}$  und  $x_{\rm o} > x_{\rm u}$  liegt, gilt:

$${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{X}(x) \ {\rm d}x.$$

• Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen  $x_{\rm u} → \hspace{0.1cm} – \hspace{0.05cm} ∞$  und  $x_{\rm o} → +∞$:

$$\int_{-\infty}^{+\infty} f_{X}(x) \ {\rm d}x = 1.$$

Verteilungsfunktion (VTF)

Die  Verteilungsfunktion  – abgekürzt  $\rm VTF$  – liefert die gleiche Information über die Zufallsgröße  $X$  wie die Wahrscheinlichkeitsdichtefunktion.

$\text{Definition:}$  Die  Verteilungsfunktion  $F_{X}(x)$  entspricht der Wahrscheinlichkeit, dass die Zufallsgröße  $X$  kleiner oder gleich einem reellen Zahlenwert  $x$  ist:

$$F_{X}(x) = {\rm Pr}( X \le x).$$

Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist  Cumulative Distribution Function  (CDF).

Die VTF weist folgende Eigenschaften auf:

• Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion  $f_{X}(x)$  durch Integration berechenbar. Es gilt:

$$F_{X}(x) = \int_{-\infty}^{x}f_X(\xi)\,{\rm d}\xi.$$

• Da die WDF nie negativ ist, steigt  $F_{X}(x)$  zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten

$$F_{X}(x → \hspace{0.1cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{X}(x → +∞) = 1.$$

• Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen:

$$f_{X}(x)=\frac{{\rm d} F_{X}(\xi)}{{\rm d}\xi}\Bigg |_{\hspace{0.1cm}x=\xi}.$$

• Für die Wahrscheinlichkeit, dass die Zufallsgröße  $X$  im Bereich zwischen  $x_{\rm u}$  und  $x_{\rm o} > x_{\rm u}$  liegt, gilt:

$${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = F_{X}(x_{\rm o}) - F_{X}(x_{\rm u}).$$

Erwartungswerte und Momente

Die Wahrscheinlichkeitsdichtefunktion bietet ebenso wie die Verteilungsfunktion sehr weitreichende Informationen über die betrachtete Zufallsgröße. Weniger, aber dafür kompaktere Informationen in Form einzelner Zahlenwerte liefern die so genannten  Erwartungswerte  und  Momente.

$\text{Definition:}$  Der  Erwartungswert  bezüglich einer beliebigen Gewichtungsfunktion  $g(x)$  kann mit der WDF  $f_{\rm X}(x)$  in folgender Weise berechnet werden:

$${\rm E}\big[g (X ) \big] = \int_{-\infty}^{+\infty} g(x)\cdot f_{X}(x) \,{\rm d}x.$$

Setzt man in diese Gleichung für  $g(x) = x^k$  ein, so erhält man das  Moment $k$-ter Ordnung:

$$m_k = {\rm E}\big[X^k \big] = \int_{-\infty}^{+\infty} x^k\cdot f_{X} (x ) \, {\rm d}x.$$

Aus dieser Gleichung erhält man

• mit  $k = 1$  für den  linearen Mittelwert:

$$m_1 = {\rm E}\big[X \big] = \int_{-\infty}^{ \rm +\infty} x\cdot f_{X} (x ) \,{\rm d}x,$$

• mit  $k = 2$  für den  quadratischen Mittelwert:

$$m_2 = {\rm E}\big[X^{\rm 2} \big] = \int_{-\infty}^{ \rm +\infty} x^{ 2}\cdot f_{ X} (x) \,{\rm d}x.$$

In Zusammenhang mit Signalen sind auch folgende Bezeichnungen üblich:

• $m_1$  gibt den  Gleichanteil  an;    bezüglich der Zufallsgröße  $X$  schreiben wir im Folgenden auch  $m_X$.
• $m_2$  entspricht der  (auf den Einheitswiderstand  $1 \ Ω$  bezogenen) Signalleistung  $P_X$.

Bezeichnet  $X$  beispielsweise eine Spannung, so hat nach diesen Gleichungen  $m_X$  die Einheit  ${\rm V}$  und die Leistung  $P_X$  die Einheit  ${\rm V}^2.$ Will man die Leistung in „Watt”  $\rm (W)$ angeben, so muss  $P_X$  noch durch den Widerstandswert  $R$  dividiert werden.

Zentralmomente

Besondere Bedeutung haben in der Statistik allgemein die so genannten  Zentralmomente, von denen viele Kenngrößen abgeleitet werden,

$\text{Definition:}$  Die  Zentralmomente  sind im Gegensatz zu den herkömmlichen Momenten jeweils auf den Mittelwert  $m_1$  bezogen. Für diese gilt mit  $k = 1, \ 2,$ ...:

$$\mu_k = {\rm E}\big[(X-m_{\rm 1})^k\big] = \int_{-\infty}^{+\infty} (x-m_{\rm 1})^k\cdot f_x(x) \,\rm d \it x.$$

• Bei mittelwertfreien Zufallsgrößen stimmen die zentrierten Momente  $\mu_k$  mit den nichtzentrierten Momente  $m_k$  überein.

• Das Zentralmoment erster Ordnung ist definitionsgemäß gleich  $\mu_1 = 0$.

• Die nichtzentrierten Momente  $m_k$  und die Zentralmomente  $\mu_k$  können direkt ineinander umgerechnet werden.  Mit  $m_0 = 1$  und  $\mu_0 = 1$  gilt dabei:

$$\mu_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot m_\kappa \cdot (-m_1)^{k-\kappa},$$

$$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$

Einige häufig benutzte Zentralmomente

Aus der letzten Definition können folgende statistische Kenngrößen abgeleitet werden:

$\text{Definition:}$  Die  Varianz  der betrachteten Zufallsgröße  $X$  ist das Zentralmoment zweiter Ordnung:

$$\mu_2 = {\rm E}\big[(X-m_{\rm 1})^2\big] = \sigma_X^2.$$

• Die Varianz  $σ_X^2$  entspricht physikalisch der „Wechselleistung” und die  Streung  $σ_X$  (oder auch  Standardabweichung) gibt den „Effektivwert” an.
• Aus dem linearen und dem quadratischen Mittelwert ist die Varianz nach dem  Satz von Steiner  in folgender Weise berechenbar:  $\sigma_X^{2} = {\rm E}\big[X^2 \big] - {\rm E}^2\big[X \big].$

$\text{Definition:}$  Die  Charliersche Schiefe  $S_X$  der betrachteten Zufallsgröße  $X$  bezeichnet das auf $σ_X^3$ bezogene dritte Zentralmoment.

• Bei symmetrischer Dichtefunktion ist die Kenngröße  $S_X$  sets Null.
• Je größer  $S_X = \mu_3/σ_X^3$  ist, um so unsymmetrischer verläuft die WDF um den Mittelwert  $m_X$.
• Beispielsweise ergibt sich für die Exponentialverteilung die Schiefe  $S_X =2$, und zwar unabhängig vom Verteilungsparameter  $λ$.

$\text{Definition:}$  Als  Kurtosis  der betrachteten Zufallsgröße  $X$  bezeichnet man den Quotienten  $K_X = \mu_4/σ_X^4$    $(\mu_4:$  Zentralmoment vierter Ordnung$)$.

• Bei einer gaußverteilten Zufallsgröße ergibt sich hierfür immer der Wert  $K_X = 3$.
• Anhand dieser Kenngröße kann man beispielsweise überprüfen, ob eine vorliegende Zufallsgröße tatsächlich gaußisch ist oder zumindest durch eine Gaußverteilung approximiert werden kann.

Zusammenstellung einiger wertkontinuierlicher Zufallsgrößen

Das Applet berücksichtigt folgende Verteilungen: 

Gaußverteilung, Gleichverteilung, Dreieckverteilung, Exponentialverteilung, Laplaceverteilung, Rayleighverteilung,
Riceverteilung, Weibullverteilung, Wigner–Halbkreisverteilung, Wigner–Parabelverteilung, Cauchyverteilung.

Einige von diesen sollen hier detailliert beschrieben werden.

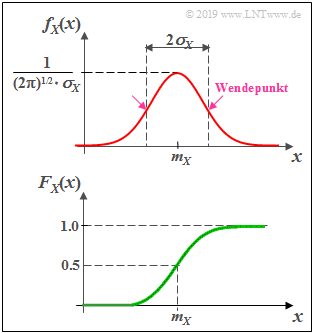
Gaußverteilte Zufallsgrößen

Gaußsche Zufallsgröße:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion   $($achsensymmetrisch um  $m_X)$

$$f_X(x) = \frac{1}{\sqrt{2\pi}\cdot\sigma_X}\cdot {\rm e}^{-(X-m_X)^2 /(2\sigma_X^2) }.$$

WDF–Parameter: 

• $m_X$  (Mittelwert bzw. Gleichanteil),
• $σ_X$  (Streuung bzw. Effektivwert).

(2)    Verteilungsfunktion   $($punktsymmetrisch um  $m_X)$

$$F_X(x)= \phi(\frac{\it x-m_X}{\sigma_X})\hspace{0.5cm}\rm mit\hspace{0.5cm}\rm \phi (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\it \pi}}\int_{-\rm\infty}^{\it x} \rm e^{\it -u^{\rm 2}/\rm 2}\,\, d \it u.$$

$ϕ(x)$:   Gaußsches Fehlerintegral (nicht analytisch berechenbar, muss aus Tabellen entnommen werden).

(3)    Zentralmomente

$$\mu_{k}=(k- 1)\cdot (k- 3) \ \cdots \ 3\cdot 1\cdot\sigma_X^k\hspace{0.2cm}\rm (falls\hspace{0.2cm}\it k\hspace{0.2cm}\rm gerade).$$

• Charliersche Schiefe  $S_X = 0$,  da  $\mu_3 = 0$  $($WDF ist symmetrisch um  $m_X)$.
• Kurtosis  $K_X = 3$,  da  $\mu_4 = 3 \cdot \sigma_X^2$  ⇒   $K_X = 3$  ergibt sich nur für die Gauß–WDF.

(4)    Weitere Bemerkungen

• Die Namensgebung geht auf den bedeutenden Mathematiker, Physiker und Astronomen Carl Friedrich Gauß zurück.
• Ist  $m_X = 0$  und  $σ_X = 1$, so spricht man oft auch von der  Normalverteilung.

• Die Streuung kann aus der glockenförmigen WDF $f_{X}(x)$ auch grafisch ermittelt werden  (als Abstand von Maximalwert und Wendepunkt).
• Zufallsgrößen mit Gaußscher WDF sind wirklichkeitsnahe Modelle für viele physikalische Größen und auch für die Nachrichtentechnik von großer Bedeutung.
• Die Summe vieler kleiner und unabhängiger Komponenten führt stets zur Gauß–WDF   ⇒   Zentraler Grenzwertsatz der Statistik   ⇒   Grundlage für Rauschprozesse.
• Legt man ein gaußverteiltes Signal zur spektralen Formung an ein lineares Filter, so ist das Ausgangssignal ebenfalls gaußverteilt.

Signal und WDF eines Gaußschen Rauschsignals

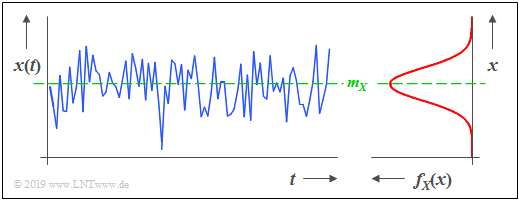
$\text{Beispiel 1:}$  Die Grafik zeigt einen Ausschnitt eines stochastischen Rauschsignals  $x(t)$, dessen Momentanwert als eine kontinuierliche Zufallsgröße  $X$  aufgefasst werden kann. Aus der rechts dargestellten WDF erkennt man:

• Es liegt eine Gaußsche Zufallsgröße vor.
• Momentanwerte um den Mittelwert  $m_X$  treten am häufigsten auf.
• Wenn zwischen den Abtastwerten  $x_ν$  der Folge keine statistischen Bindungen bestehen, bezeichnet man ein solches Signal auch als „Weißes Rauschen”.

Gleichverteilte Zufallsgrößen

Gleichverteilung:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion

• Die Wahrscheinlichkeitsdichtefunktion (WDF)  $f_{X}(x)$  ist im Bereich von  $x_{\rm min}$  bis  $x_{\rm max}$  konstant gleich  $1/(x_{\rm max} - x_{\rm min})$  und außerhalb Null.
• An den Bereichsgrenzen ist für  $f_{X}(x)$  jeweils nur der halbe Wert  (Mittelwert zwischen links- und rechtsseitigem Grenzwert)  zu setzen.

(2)    Verteilungsfunktion

• Die Verteilungsfunktion (VTF) steigt im Bereich von  $x_{\rm min}$  bis  $x_{\rm max}$  linear von Null auf  $1$  linear an.

(3)    Momente und Zentralmomente

• Mittelwert und Streuung haben bei der Gleichverteilung die folgenden Werte:

$$m_X = \frac{\it x_ {\rm max} \rm + \it x_{\rm min}}{2},\hspace{0.5cm} \sigma_X^2 = \frac{(\it x_{\rm max} - \it x_{\rm min}\rm )^2}{12}.$$

• Bei symmetrischer WDF   ⇒   $x_{\rm min} = -x_{\rm max}$  ist der Mittelwert  $m_X = 0$  und die Varianz  $σ_X^2 = x_{\rm max}^2/3.$
• Aufgrund der Symmetrie um den Mittelwert  $m_X$  ist die Charliersche Schiefe  $S_X = 0$.
• Die Kurtosis ist mit   $K_X = 1.8$  deutlich kleiner als bei der Gaußverteilung, weil die WDF–Ausläufer fehlen.

(4)    Weitere Bemerkungen

• Für die Modellierung übertragungstechnischer Systeme sind gleichverteilte Zufallsgrößen die Ausnahme. Ein Beispiel für eine tatsächlich (nahezu) gleichverteilte Zufallsgröße ist die Phase bei kreissymmetrischen Störungen, wie sie beispielsweise bei  Quadratur–Amplitudenmodulationsverfahren  (QAM) auftreten.

• Die Bedeutung gleichverteilter Zufallsgrößen für die Informations– und Kommunikationstechnik liegt eher darin, dass diese WDF–Form aus Sicht der Informationstheorie unter der Nebenbedingung „Spitzenwertbegrenzung” ein Optimum bezüglich der differentiellen Entropie darstellt.

• In der Bildverarbeitung & Bildcodierung wird häufig mit der Gleichverteilung anstelle der tatsächlichen, meist sehr viel komplizierteren Verteilung des Originalbildes gerechnet, da der Unterschied des Informationsgehaltes zwischen einem natürlichen Bild und dem auf der Gleichverteilung basierenden Modell relativ gering ist.

• Bei der Simulation nachrichtentechnischer Systeme verwendet man häufig auf der Gleichverteilung basierende „Pseudo–Zufallsgeneratoren” (die relativ einfach zu realisieren sind), woraus sich andere Verteilungen  (Gaußverteilung, Exponentialverteilung, etc.)  leicht ableiten lassen.

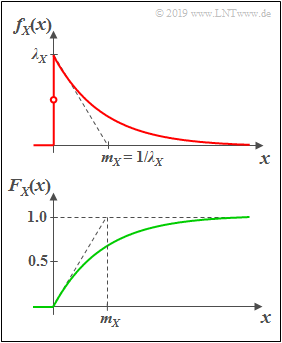
Exponentialverteilte Zufallsgrößen

(1)    Wahrscheinlichkeitsdichtefunktion

Exponentialverteilung:  WDF und VTF

Eine exponentialverteilte Zufallsgröße  $X$  kann nur nicht–negative Werte annehmen. Für  $x>0$  hat die WDF den folgenden Verlauf hat:

$$f_X(x)=\it \lambda_X\cdot\rm e^{\it -\lambda_X \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$

• Je größer der Verteilungsparameter  $λ_X$  ist, um so steiler erfolgt der Abfall.
• Definitionsgemäß gilt  $f_{X}(0) = λ_X/2$, also der Mittelwert aus linksseitigem Grenzwert  $(0)$  und rechtsseitigem Grenzwert  $(\lambda_X)$.

(2)    Verteilungsfunktion

Durch Integration über die WDF erhält man für  $x > 0$:

$$F_{X}(x)=1-\rm e^{\it -\lambda_X\hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$

(3)    Momente und Zentralmomente

• Die  Momente  der (einseitigen) Exponentialverteilung sind allgemein gleich:

$$m_k = \int_{-\infty}^{+\infty} x^k \cdot f_{X}(x) \,\,{\rm d} x = \frac{k!}{\lambda_X^k}.$$

• Daraus und aus dem Satz von Steiner ergibt sich für Mittelwert und Streuung:

$$m_X = m_1=\frac{1}{\lambda_X},\hspace{0.6cm}\sigma_X^2={m_2-m_1^2}={\frac{2}{\lambda_X^2}-\frac{1}{\lambda_X^2}}=\frac{1}{\lambda_X^2}.$$

• Die WDF ist hier deutlich unsymmetrisch. Für die Charliersche Schiefe ergibt sich  $S_X = 2$.
• Die Kurtosis ist mit   $K_X = 9$  deutlich größer als bei der Gaußverteilung, weil die WDF–Ausläufer sehr viel weiter reichen.

(4)    Weitere Bemerkungen

• Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen; in diesem Zusammenhang ist auch der Begriff „Lebensdauerverteilung” üblich.
• Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit  $t$, die bis zum Ausfall einer Komponente vergeht.
• Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Laplaceverteilung in Zusammenhang steht.

Laplaceverteilte Zufallsgrößen

Laplaceverteiung:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion

Wie aus der Grafik zu ersehen ist die Laplaceverteilung eine „zweiseitige Exponentialverteilung”:

$$f_{X}(x)=\frac{\lambda_X} {2}\cdot{\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}.$$

• Der Maximalwert ist hier  $\lambda_X/2$.
• Die Tangente bei  $x=0$  schneidet die Abszisse wie bei der Exponentialverteilung bei  $1/\lambda_X$.

(2)    Verteilungsfunktion

$$F_{X}(x) = {\rm Pr}\big [X \le x \big ] = \int_{-\infty}^{x} f_{X}(\xi) \,\,{\rm d}\xi$$

$$\Rightarrow \hspace{0.5cm} F_{X}(x) = 0.5 + 0.5 \cdot {\rm sign}(x) \cdot \big [ 1 - {\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}\big ]$$

$$\Rightarrow \hspace{0.5cm} F_{X}(-\infty) = 0, \hspace{0.5cm}F_{X}(0) = 0.5, \hspace{0.5cm} F_{X}(+\infty) = 1.$$

(3)    Momente und Zentralmomente

• Für ungeradzahliges  $k$  ergibt sich bei der Laplaceverteilung aufgrund der Symmetrie stets  $m_k= 0$. Unter Anderem:  Linearer Mittelwert  $m_X =m_1 = 0$.

• Für geradzahliges  $k$  stimmen die Momente von Laplaceverteilung und Exponentialverteilung überein:  $m_k = {k!}/{\lambda^k}$.

• Für die Varianz  $(=$ Zentralmoment zweiter Ordnung $=$ Moment zweiter Ordnung$)$  gilt:  $\sigma_X^2 = {2}/{\lambda_X^2}$   ⇒   doppelt so groß wie bei der Exponentialverteilung.

• Für die Charliersche Schiefe ergibt sich hier aufgrund der symmetrischen WDF   $S_X = 0$.

• Die Kurtosis ist mit  $K_X = 6$  deutlich größer als bei der Gaußverteilung, aber kleiner als bei der Exponentialverteilung.

(4)    Weitere Bemerkungen

• Die Momentanwerte von Sprach– und Musiksignalen sind mit guter Näherung laplaceverteilt.
  Siehe Lernvideo  Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion,  Teil 2.
• Durch eine zusätzliche Diracfunktion bei  $x=0$  lassen sich auch Sprachpausen modellieren.

Kurzbeschreibung weiterer Verteilungen

$\text{(A) Rayleighverteilung}$     Genauere Beschreibung

• Anwendung:     Modellierung des Mobilfunkkanals (nichtfrequenzselektives Fading, nur Dämpfungs–, Beugungs– und Brechungseffekte, keine Sichtverbindung)

• Wahrscheinlichkeitsdichtefunktion:

$$f_X(x) = \left\{ \begin{array}{c} x/\lambda_X^2 \cdot {\rm e}^{- x^2/(2 \hspace{0.05cm}\cdot\hspace{0.05cm} \lambda_X^2)} \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.1cm} x\hspace{-0.05cm} \ge \hspace{-0.05cm}0, \\ {\rm f\ddot{u}r}\hspace{0.1cm} x \hspace{-0.05cm}<\hspace{-0.05cm} 0. \\ \end{array}.$$

$\text{B) Riceverteilung}$     Genauere Beschreibung

• Anwendung:     Modellierung des Mobilfunkkanals (nichtfrequenzselektives Fading, nur Dämpfungs–, Beugungs– und Brechungseffekte, mit Sichtverbindung)

• Wahrscheinlichkeitsdichtefunktion  $(\rm I_0$  bezeichnet die modifizierte Bessel–Funktion nullter Ordnung$)$:

$$f_X(x) = \frac{x}{\lambda_X^2} \cdot {\rm exp} \big [ -\frac{x^2 + C_X^2}{2\cdot \lambda_X^2}\big ] \cdot {\rm I}_0 \left [ \frac{x \cdot C_X}{\lambda_X^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$

$\text{C) Weibullverteilung}$     [Genauere Beschreibung]

• Anwendung:     Modellierung des Mobilfunkkanals (nichtfrequenzselektives Fading, nur Dämpfungs–, Beugungs– und Brechungseffekte, mit Sichtverbindung)

• Wahrscheinlichkeitsdichtefunktion  $(\rm I_0$  bezeichnet die modifizierte Bessel–Funktion nullter Ordnung$)$:

$$f_X(x) = \frac{x}{\lambda_X^2} \cdot {\rm exp} \big [ -\frac{x^2 + C_X^2}{2\cdot \lambda_X^2}\big ] \cdot {\rm I}_0 \left [ \frac{x \cdot C_X}{\lambda_X^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$

Versuchsdurchführung

• Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
• Lösung nach Drücken von „Musterlösung”.
• Im Folgenden steht  $\text{Rot}$  für die Zufallsgröße  $X$  und  $\text{Blau}$  für  $Y$.

Die Nummer 0 entspricht einem „Reset”:

• Gleiche Einstellung wie beim Programmstart.
• Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.

Was noch?

(1)  Wählen Sie  $\text{Rot: Gaußverteilung}\ (m_X = 1, \ \sigma_X = 0.4)$  und $\text{Blau: Gleichverteilung}\ (y_{\rm min} = -2, \ y_{\rm max} = +3)$. Interpretieren Sie die  $\rm WDF$–Grafik.

•  $\text{Gaußverteilung}$:  Das  $\rm WDF$–Maximum ist gleich  $f_{X}(x = m_X) = \sqrt{1/(2\pi \cdot \sigma_X^2)} = 0.9974 \approx 1$.
•  $\text{Gleichverteilung}$:  Alle  $\rm WDF$–Werte sind im Bereich  $-2 < y < +3$  gleich  $0.2$. An den Rändern gilt  $f_Y(-2) = f_Y(+3)= 0.1$  (halber Wert).

(2)  Gleiche Einstellung wie bei  (1). Wie groß sind die Wahrscheinlichkeiten  ${\rm Pr}(X = 0)$  und  ${\rm Pr}(0.5 \le X \le 1.5)$  sowie  ${\rm Pr}(Y = 0)$  und  ${\rm Pr}(0.5 \le Y \le 1.5)$ .

•  ${\rm Pr}(X = 0)={\rm Pr}(Y = 0) \equiv 0$   ⇒   Wahrscheinlichkeit einer wertdiskreten Zufallsgröße, dass diese exakt einen bestimmten Wert annimmt.
•  Die beiden anderen Wahrscheinlichkeiten können durch Integration über die WDF im Bereich  $+0.5\ \text{...} \ +\hspace{-0.1cm}1.5$  ermittelt werden.
•  Oder:  ${\rm Pr}(0.5 \le X \le 1.5)= F_X(1.5) - F_X(0.5) = 0.8944-0.1056 = 0.7888$. Entsprechend:  ${\rm Pr}(0.5 \le Y \le 1.5)= 0.7-0.5=0.2$.

(3)  Gleiche Einstellungen wie bisher. Wie muss die Streung  $\sigma_X$  verändert werden, damit bei gleichem Mittelwert  $m_X$  für den quadratische Mittelwert gilt:  $P_X=2$ ?

•  Nach dem Satz von Steiner gilt:  $P_X=m_X^2 + \sigma_X^2$   ⇒   $\sigma_X^2 = P_X-m_X^2 = 2 - 1^2 = 1$   ⇒   $\sigma_X = 1$.

(4)  Gleiche Ausgangslage wie bisher:  Wie müssen die Parameter  $y_{\rm min}$  und  $y_{\rm max}$  der Gleichverteilung geändert werden, damit sich  $m_Y = 0$  und $\sigma_Y^2 = 0.75$ ergibt?

•  Ausgehend von der bisherigen Einstellung  $(y_{\rm min} = -2, \ y_{\rm max} = +3)$  verändern wir  $y_{\rm max}$, bis sich  $\sigma_Y^2 = 0.75$  einstellt.   ⇒     $y_{\rm max} = 1$.
•  Die Breite des Rechtecks ist nun  $3$. Den gewünschten Mittelwert   $m_Y = 0$  erreicht man durch eine Verschiebung:  $y_{\rm min} = -1.5, \ y_{\rm max} = +1.5$.
•  Sie könnten auch berücksichtigen, dass für eine mittelwertfreie Zufallsgröße  $(y_{\rm min} = -y_{\rm max})$  folgende Gleichung gilt:   $\sigma_Y^2 = y_{\rm max}^2/3$.

(5)  Bei welchen der einstellbaren Verteilungen ist die Charliersche Schiefe  $S \ne 0$ ?

•  Die Charliersche Schiefe bezeichnet das auf  $σ_X^3$  bezogene dritte Zentralmoment:  $S_X = \mu_3/σ_X^3$  $($gültig für die Zufallsgröße  $X)$.
•  Ist die WDF  $f_X(x)$  um den Mittelwert  $m_X$  symmetrisch, dann ist die Kenngröße  $S_X$  stets Null.
•  Exponentialverteilung:  $S_X =2$;  Rayleighverteilung:  $S_X =0.631$  $($jeweils unabhängig von $λ_X)$;   Riceverteilung:  $S_X >0$  $($abhängig von $C_X, \ λ_X)$.
•  Bei der Weibullverteilung kann die Charliersche Schiefe  $S_X$  abhängig vom WDF–Parameter  $K_X$  Null, positiv oder negativ sein.

(6)  Wählen Sie  $\text{Rot: Gaußverteilung}\ (m_X = 1, \ \sigma_X = 0.4)$  und $\text{Blau: Gaußverteilung}\ (m_X = 0, \ \sigma_X = 1)$ . Wie groß ist jeweils die Kurtosis?

•  Bei jeder  $\text{Gaußverteilung}$  hat die Kurtosis den gleichen Wert:   $K_X = K_Y =3$. Man bezeichnet deshalb  $K−3$  als die „Gaußabweichung”.
• Anhand dieser Kenngröße kann man überprüfen, ob eine vorliegende Zufallsgröße durch eine Gaußverteilung approximiert werden kann.

(7)  Bei welchen Verteilungen ergibt sich beispielsweise ein deutlich kleinerer Kurtosiswert als  $K=3$? Und bei welchen Verteilungen ein deutlich größerer?

•  $K<3$  ergibt sich immer dann, wenn die WDF–Werte stärker um den Mittelwert konzentriert sind als bei der Gaußverteilung.
•  Dies trifft zum Beispiel für die Gleichverteilung  $(K=1.8)$  und für die Dreieckverteilung  $(K=2.4)$  zu.
•  Sind die WDF–Ausläufer ausgeprägter als bei „Gauß”, so ist der Kurtosiswert  $K>3$. Beispiel:  Exponentialverteilung  $(K=9)$.

(8)  Wählen Sie  $\text{Rot: Exponentialverteilung}\ (\lambda_X = 1)$  und $\text{Blau: Laplaceverteilung}\ (\lambda_Y = 1)$ . Interpretieren Sie die Unterschiede?

•  Die Laplaceverteilung ist symmetrisch um ihren Mittelwert  $(S_Y=0, \ m_Y=0)$  im Gegensatz zur Exponentialverteilung  $(S_X=2, \ m_X=1)$.
•  Die geraden Momente  $m_2, \ m_4, \ \text{...}$  sind gleich, also auch der quadratische Mittelwert:  $P_X=P_Y=2$. Nicht aber die Varianzen:  $\sigma_X^2 =1, \ \sigma_Y^2 =2$.
•  Die Wahrscheinlichkeiten ${\rm Pr}(|X| < 2) = F_X(2) = 0.865$  und  ${\rm Pr}(|Y| < 2) = F_Y(2) - F_Y(-2)= 0.9323 - 0.0677 = 0.865$  sind gleich.
•  Bei der Laplaceverteilung sind die Werte enger um den Mittelwert konzentriert als bei der Exponentialverteilung:  $K_Y =6 < K_X = 9$.

(9)  Wählen Sie  $\text{Rot: Riceverteilung}\ (\lambda_X = 1, \ C_X = 1)$  und  $\text{Blau: Rayleighverteilung}\ (\lambda_Y = 1)$. Variieren Sie  $C_X$. Interpretieren Sie die Unterschiede?

•   Mit  $C_X = 0$  geht die Riceverteilung exakt in die Rayleighverteilung über. Ein größeres  $C_X$  „verbessert” die Performance, z.B. beim Mobilfunk.
•   Bei „Rayleigh” und „Rice” ist die Abszisse der (zeitabhängige) Betrag  $A$  des Empfangssignals. Günstig ist, wenn  ${\rm Pr}(A \le A_0)$  klein ist  $(A_0$  vorgegeben$)$.
•   Bei  $C_X \ne 0$  und gleichem  $\lambda$  liegt die Rice–VTF im gesamten Definitionsbereich unterhalb der Rayleigh–VTF   ⇒   kleineres  ${\rm Pr}(A \le A_0)$  für alle  $A_0$.

(10)  Wählen Sie  $\text{Rot: Riceverteilung}\ (\lambda_X = 0.6, \ C_X = 2)$. Durch welche Verteilung  $F_Y(y)$  lässt sich diese Riceverteilung gut approximieren?

•   Die Kurtosis   $K_X = 2.9539 \approx 3$  weist auf die Gaußverteilung hin. Günstige Parameter:  $m_Y = 2.15 > C_X, \ \sigma_Y = \lambda_X = 0.6$.
•   Je größer der Quotient  $C_X/\lambda_X$  ist, umso besser wird die Riceverteilung durch eine Gaußverteilung angenähert.
•   Bei großem   $C_X/\lambda_X$  hat die die Riceverteilung keine Ähnlichkeit mehr mit der Rayleighverteilung.

(11)  Wählen Sie  $\text{Rot: Weibullverteilung}\ (\lambda_X = 1, \ k_X = 1)$  und  $\text{Blau: Weibullverteilung}\ (\lambda_Y = 1, \ k_Y = 2)$. Interpretieren Sie die Ergebnisse.

•   $f_X(x)$  ist identisch mit der Exponentialverteilung und  $f_Y(y)$  mit der Rayleighverteilung.
• Nach bestmöglicher Anpassung unterscheiden sich allerdings die Parameter  $\lambda_{\rm Weibull} = 1$  und  $\lambda_{\rm Rayleigh} = 0.7$.
•   Für  $K_X < 1$  gilt zudem  $f_X(x = 0) \to \infty$. Dies wirkt sich allerdings nicht durch unendlich große Momente aus.

(12)  Wählen Sie  $\text{Rot: Weibullverteilung}\ (\lambda_X = 1, \ k_X = 1.6)$  und  $\text{Blau: Weibullverteilung}\ (\lambda_Y = 1, \ k_Y = 5.6)$. Interpretieren Sie die Charliersche Schiefe.

•   Man beobachtet: Für  $K < K_*$  ist die Charliersche Schiefe positiv und für  $K > K_*$  negativ. Es gilt näherungsweise  $K_* = 3.6$.

(13)  Wählen Sie  $\text{Rot: Halbkreisverteilung}\ (m_X = 0, \ R_X = 1)$  und  $\text{Blau: Parabelverteilung}\ (m_Y = 0, \ R_Y = 1)$. Variieren Sie jeweils den $R$–Parameter.

•   Die WDF ist jeweils mittelwertfrei und symmetrisch  $(S_X = S_Y =0)$  mit  $\sigma_X^2 = 0.25, \ K_X = 2$  bzw.  $\sigma_Y^2 = 0.2, \ K_Y \approx 2.2$.

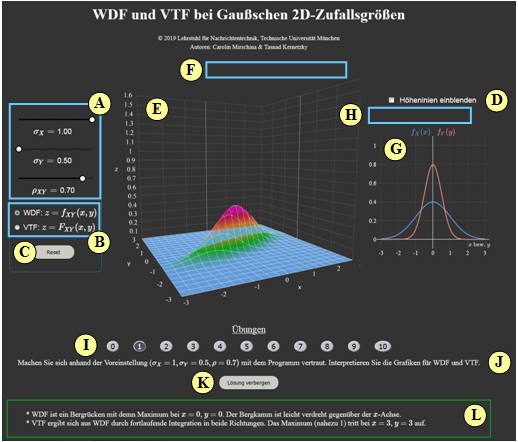
Zur Handhabung des Applets

    (A)     Parametereingabe per Slider:  $\sigma_X$,  $\sigma_Y$ und  $\rho$

    (B)     Auswahl:  Darstellung von WDF oder VTF

    (C)     Reset:  Einstellung wie beim Programmstart

    (D)     Höhenlinien darstellen anstelle von „1D-WDF”

    (E)     Darstellungsbereich für „2D-WDF”

    (F)     Manipulation der 3D-Grafik (Zoom, Drehen, ...)

    (G)     Darstellungsbereich für „1D-WDF” bzw. „Höhenlinien”

    (H)     Manipulation der 2D-Grafik („1D-WDF”)

    ( I )     Bereich für die Versuchsdurchführung: Aufgabenauswahl

    (J)     Bereich für die Versuchsdurchführung: Aufgabenstellung

    ( L)     Bereich für die Versuchsdurchführung: Musterlösung







Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2019 wurde das Programm von Matthias Niller  im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch  Studienzuschüsse  der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab