Exercise 2.2: Modulation Depth

• Return to book

Modulationsgrad-Definition bei ZSB–AM

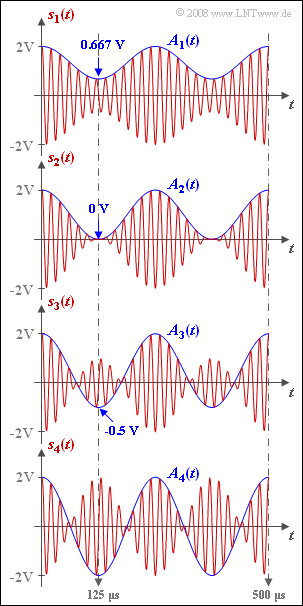
Die Grafik zeigt ZSB–amplitudenmodulierte Signale  $s_1(t)$  bis  $s_4(t)$  mit unterschiedlichem Modulationsgrad  $m$. Nachrichtensignal  $q(t)$  und Trägersignal  $z(t)$  seien jeweils cosinusförmig:

$$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$

$$z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$

Das modulierte Signal (Sendesignal) lautet mit dem im Modulator zugesetzten Gleichanteil  $A_{\rm T}$:

$$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$

Bei den Grafiken wurde zur Normierung gewählt:

$$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$

• Ist der Modulationsgrad  $m ≤ 1$, so ist  $A(t)= q(t) + A_{\rm T}$  gleich der Hüllkurve  $a(t)$.
• Dagegen gilt für den Modulationsgrad  $m > 1$:

$$a(t ) = |A(t)|\hspace{0.05cm}.$$

• Der Cosinusverlauf  $A(t)$  schwankt zwischen  $A_{\rm max}$  und  $A_{\rm min}$; wegen der Normierung ist stets  $A_{\rm max} = 2 \ \rm V$.
• Die Minimalwerte von  $A(t)$  treten bei der halben Periodendauer des Quellensignals  $($also für  $t = 125 \ \rm µ s)$  auf:

$$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$

• Die Zahlenwerte sind in der Grafik angegeben.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Zweiseitenband-Amplitudenmodulation.
• Bezug genommen wird insbesondere auf die Seite  ZSB-Amplitudenmodulation mit Träger.

Fragebogen

1

Bestimmen Sie für die Signale  $s_1(t)$,  $s_2(t)$,  $s_3(t)$  jeweils den Modulationsgrad.

$m_1 \ = \ $

$m_2 \ = \ $

$m_3 \ = \ $

2

Welche Aussagen treffen für das Signal  $s_4(t)$  zu?

	Es handelt sich um  „ZSB–AM ohne Träger”.
	Der Modulationsgrad ist  $m = 0$.
	Der Modulationsgrad  $m$  ist unendlich groß.

3

Es gelte nun  $A_{\rm T} = A_{\rm N} = 1\ \rm V$, also  $m = 1$.  Wie lautet das Spektrum  $S_+(f)$  des analytischen Signals?
Welche Diracgewichte treten bei  $f_{\rm T}$  sowie bei  $f_{\rm T}± f_{\rm N}$  auf?

$S_+(f_{\rm T}) \ = \ $ $\ \text{V}$

$S_+(f_{\rm T} ± f_{\rm N}) \ = \ $ $\ \text{V}$

4

Es gelte weiter  $m = 1$.  Welcher Anteil  $P_{\rm T}/P_{\rm S}$  der gesamten Sendeleistung  $P_{\rm S}$  geht allein auf den Träger zurück, der nicht zur Demodulation genutzt werden kann?

$P_{\rm T}/P_{\rm S} \ = \ $

5

Verallgemeinern Sie das Ergebnis aus  (4)  für einen beliebigen Modulationsgrad  $m$.
Welche Leistungsverhältnisse ergeben sich für  $m = 0.5$,  $m = 3$  und  $m → ∞$ ?

$m = 0.5\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m = 3.0\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m → ∞ \text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

6

Welche der nachfolgenden Bewertungen erscheinen Ihnen nach den bisherigen Berechnungen als sinnvoll?

	$m ≈ 1$  ist aus energetischen Gründen günstiger als ein kleines  $m$.
	Nur bei Hüllkurvendemodulation ist der Träger sinnvoll.

Musterlösung

Solution

(1)  Aus den beiden Gleichungen

$$A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$

folgt direkt

$$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2,\hspace{0.3cm} A_{\rm T} = (A_{\rm max} + A_{\rm min})/2\hspace{0.05cm}.$$

Somit lautet der Modulationsgrad

$$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$

Mit den angegebenen Zahlenwerten erhält man: $$m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm}\underline {= 1.0}\hspace{0.05cm}, \hspace{0.5cm} m_3 = \frac{2\,{\rm V} -(-1\,{\rm V})}{2\,{\rm V} + (-1\,{\rm V})} \hspace{0.15cm}\underline{=3.0}\hspace{0.05cm}.$$

(2)  Richtig sind die Aussagen 1 und 3:

• In diesem Fall ist $A_{\rm T} = 0$, das heißt, es liegt tatsächlich eine „ZSB–AM ohne Träger” vor.
• Der Modulationsgrad $m = A_{\rm N}/A_{\rm T}$ ist unendlich groß.

Spektrum des analytischen Signals

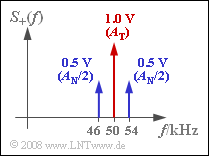
(3)  Das Spektrum $S_+(f)$ setzt sich für jeden Modulationsgrad $m$ aus drei Diraclinien zusammen mit folgenden Gewichten:

• $A_{\rm T}$ (bei $f = f_{\rm T}$)
• $m/2 · A_{\rm T}$ (bei $f = f_{\rm T} ± f_{\rm N}$).

Für $m = 1$ ergeben sich die Gewichte entsprechend der Skizze:

• $S_+(f_{\rm T}) = 1\ \rm V$,
• $S_+(f_{\rm T} ± f_{\rm T}) = 0.5\ \rm V$.

(4)  Die auf den Widerstand $1 \ Ω$ bezogene Leistung (Quadrat des Effektivwertes) einer harmonischen Schwingung mit der Amplitude $A_{\rm T} = 1 \ \rm V$ beträgt:

$$P_{\rm T} ={A_{\rm T}^2}/{2} = 0.5\,{\rm V}^2 \hspace{0.05cm}.$$

In gleicher Weise erhält man für die Leistungen des unteren und des oberen Seitenbandes:

$$P_{\rm USB} = P_{\rm OSB} =({A_{\rm N}}/{2})^2/2 = 0.125\,{\rm V}^2 \hspace{0.05cm}.$$

Das gesuchte Verhältnis für $m=1$ ist somit:

$${P_{\rm T}}/{P_{\rm S}}= \frac{P_{\rm T}}{P_{\rm USB} + P_{\rm T}+ P_{\rm OSB}}= \frac{0.5\,{\rm V}^2}{0.125\,{\rm V}^2 + 0.5\,{\rm V}^2+ 0.125\,{\rm V}^2}= 2/3\hspace{0.15cm}\underline { = 0.667}\hspace{0.05cm}.$$

(5)  Mit den Diracgewichten $m/2 · A_{\rm T}$ der beiden Seitenbänder entsprechend der Teilaufgabe (3) erhält man:

$${P_{\rm T}}/{P_{\rm S}}= \frac{A_{\rm T}^2/2}{A_{\rm T}^2/2 + 2 \cdot (m/2)^2 \cdot A_{\rm T}^2/2}= \frac{2}{2 + m^2}\hspace{0.05cm}.$$

Dies führt zu den Zahlenwerten $8/9 = 0.889$ (für $m = 0.5$),     $2/11 = 0.182$ (für $m = 3$) und     $0$ (für m → ∞).

(6)  Beide Aussagen treffen zu:

• Die Zusetzung des Trägers macht nur Sinn, um den einfacheren Hüllkurvendemodulator verwenden zu können. Dies geht nur für $m \le 1$.
• Ist dagegen der Modulationsgrad $m > 1$ und somit der Einsatz eines Synchrondemodulators erforderlich, sollte man aus energetischen Gründen auf den Träger (fast) ganz verzichten.
• Ebenso ist bei Anwendung eines Hüllkurvendemodulators aus energetischen Gründen ein möglichst großer Modulationsgrad $m < 1$   ⇒   $m \to 1$ anzustreben.
• Allerdings kann durch einen kleinen Restträger die Trägerrückgewinnung erleichtert werden, die beim Synchrondemodulator zur Frequenz  und Phasensynchronisation benötigt wird. Die zweite Aussage ist somit nur bedingt als richtig zu bewerten.