Exercise 2.5: Scatter Function

• Return to book

Verzögerungs–Doppler–Funktion

Für den Mobilfunkkanal als zeitvariantes System gibt es insgesamt vier Systemfunktionen, die über die Fouriertransformation miteinander verknüpft sind. Mit der in unserem Lerntutorial formalisierten Nomenklatur sind diese:

• die zeitvariante Impulsantwort  $h(\tau, \hspace{0.05cm}t)$, die wir hier auch mit  $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$  bezeichnen,
• die Verzögerungs–Doppler–Funktion  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$,
• die Frequenz–Doppler–Funktion  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$,
• die zeitvariante Übertragungsfunktion  $\eta_{\rm FZ}(f,\hspace{0.05cm}t)$  oder  $H(f, \hspace{0.05cm}t)$.

Die Indizes stehen für die Verzögerung  $\tau$, die Zeit  $t$, die Frequenz  $f$  sowie die Dopplerfrequenz  $f_{\rm D}$.

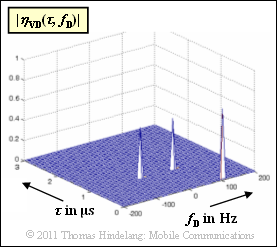
Gegeben ist die Verzögerungs–Doppler–Funktion  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$  entsprechend der oberen Grafik:

$$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2}} \cdot \delta (\tau) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})-$$

$$\hspace{1.75cm} \ - \ \hspace{-0.1cm} \frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})- \frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) \hspace{0.05cm}.$$

In der Literatur wird  $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$  oft auch Scatter–Funktion genannt und mit  $s(\tau, \hspace{0.05cm}f_{\rm D})$  bezeichnet.

In dieser Aufgabe sollen die zugehörige Verzögerungs–Zeit–Funktion  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$  und die Frequenz–Doppler–Funktion  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$  ermittelt werden.

Hinweise:

• Die Aufgabe soll den Lehrstoff des Kapitels  Das GWSSUS–Kanalmodell verdeutlichen.
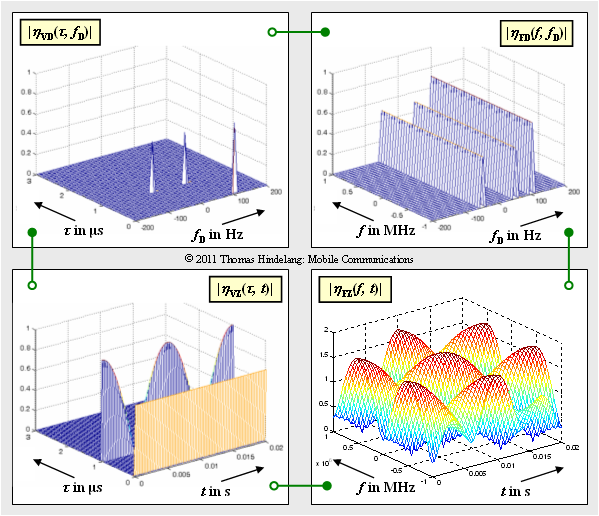
• Der Zusammenhang zwischen den einzelnen Systemfunktionen ist in der  Grafik auf der ersten Seite  dieses Kapitels angegeben.
• Beachten Sie, dass oben die Betragsfunktion  $|\eta_{\rm VD}(\tau, \hspace{0.05cm} f_{\rm D})|$  dargestellt ist, so dass negative Gewichte der Diracfunktionen nicht zu erkennen sind.

Fragebogen

1

Bei welchen  $\tau$–Werten hat die 2D–Impulsantwort  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$  Anteile? Bei

	$\tau = 0$,
	$\tau = 1 \ \rm µ s$,
	anderen $\tau$–Werte.

2

Berechnen Sie  $|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm}t)|$. Welche der folgenden Aussagen treffen zu?

	$|\eta_{\rm VZ}(\tau = 0,\hspace{0.05cm} t)|$  ist unabhängig von  $t$.
	Es gilt  $\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$.
	Es gilt  $\eta_{\rm VZ}(\tau = 0, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$.

3

Berechnen Sie  $|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$. Welche der Aussagen treffen zu?

	$|\eta_{\rm VZ}(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)|$  ist unabhängig von  $t$.
	Es gilt  $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \cos {(2\pi f_0 t)}$.
	Es gilt  $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, \hspace{0.05cm}t) = A \cdot \sin {(2\pi f_0 t)}$.

4

Betrachten Sie nun die Frequenz–Doppler–Darstellung  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D})$. Für welche  $f_{\rm D}$–Werte ist diese Funktion ungleich Null? Für

	$f_{\rm D} = 0$,
	$f_{\rm D} = ± 50 \ \rm Hz$,
	$f_{\rm D} = ± 100 \ \rm Hz$.

5

Welche der folgenden Aussagen gelten für  $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$?

	$|\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D} = 100 \ \rm Hz)|$  ist unabhängig von  $f_{\rm D}$.
	Es gilt  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \cos {(2\pi t_0 f)}$.
	Es gilt  $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 50 \ {\rm Hz}) = A \cdot \sin {(2\pi t_0 f)}$.

6

Wie kommt man zur zeitvarianten Übertragungsfunktion  $\eta_{\rm FZ}(f, \hspace{0.05cm}t)$?

	Durch Fouriertransformation von  $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D})$  bezüglich  $\tau$.
	Durch Fouriertransformation von  $\eta_{\rm VZ}(\tau, \hspace{0.05cm}t)$  bezüglich  $\tau$.
	Durch Fourierrücktransformation von  $\eta_{\rm FD}(f,\hspace{0.05cm} f_{\rm D})$  bezüglich  $f_{\rm D}$.

Musterlösung

Solution

(1)  Die zeitvariante Impulsantwort $h(\tau, \hspace{0.05cm} t) = \eta_{\rm VZ}(\tau, \hspace{0.05cm} t)$ ist die Fourierrücktransformierte der Verzögerungs–Doppler–Funktion $\eta_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) = s(\tau, \hspace{0.05cm} f_{\rm D})$:

$$\eta_{\rm VZ}(\tau, \hspace{0.05cm} t) \hspace{0.2cm} \stackrel{t, \hspace{0.02cm}f_{\rm D}}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.$$

• Dementsprechend ist $\eta_{\rm VZ}(\tau,\hspace{0.05cm} t)$ für alle Werte von $\tau$ identisch $0$, für die auch in der Scatter–Funktion $\eta_{\rm VD}(\tau, f_{\rm D})$ keine Anteile zu erkennen sind.
• Richtig sind also die Lösungsvorschläge 1 und 2: Nur für $\tau = 0$ und $\tau = 1 \ \rm \mu s$ besitzt die zeitvariante Impulsantwort endliche Werte.

(2)  Für die Verzögerung $\tau = 0$ besteht die Scatter–Funktion ($\eta_{\rm VD}$) aus einem einzigen Dirac bei $f_{\rm D} = 100 \ \rm Hz$.

• Für die gesuchte Zeitfunktion gilt gemäß dem zweiten Fourierintegral:

$$\eta_{\rm VZ}(\tau = 0, t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2}} \cdot \int\limits_{-\infty}^{+\infty} \delta (f_{\rm D} - 100\,{\rm Hz}) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}f_{\rm D} =\frac{1}{\sqrt{2}} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi t \hspace{0.05cm}\cdot \hspace{0.05cm}100\,{\rm Hz}} .$$

• Richtig ist demzufolge der Lösungsvorschlag 1.

(3)  Bei der Verzögerungszeit $\tau = 1 \ \rm µ s$ besteht die Verzögerungs–Doppler–Funktion dagegen aus zwei Diracfunktionen bei $±50 \ \rm Hz$, jeweils mit dem Gewicht $-0.5$.

• Die Zeitfunktion ergibt sich damit zu

$$\eta_{\rm VZ}(\tau = 1\,{\rm \mu s}, t) = - \cos( 2 \pi t \cdot 50\,{\rm Hz})\hspace{0.05cm}.$$

• Diese Funktion lässt sich mit $A = -1$ und $f_0 = 50 \ \rm Hz$ gemäß Lösungsvorschlag 2 darstellen.

(4)  Die drei Diracfunktionen $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ liegen bei den Dopplerfrequenzen $+100 \ \rm Hz$, $+50 \ \rm Hz$ und $-50 \ \rm Hz$.

• Für alle anderen Dopplerfrequenzen muss deshalb auch $\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}) \equiv 0$ sein.
• Richtig ist hier also der Lösungsvorschlag 2.

(5)  Betrachtet man die Scatter–Funktion $\eta_{\rm VD}(\tau, \hspace{0.05cm}f_{\rm D})$ in Richtung der $\tau$–Achse, so erkennt man bei den Dopplerfrequenzen $100 \ \rm Hz$ und $±50 \ \rm Hz$ nur jeweils eine Diracfunktion.

• Hier ergeben sich in Abhängigkeit von $f$ jeweils komplexe Exponentialschwingungen mit konstantem Betrag (woraus folgt, dass der Lösungsvorschlag 1 richtig ist):

$$|\eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D} = 100\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{\sqrt{2}} = {\rm const.}$$

$$| \eta_{\rm FD}(f, \hspace{0.05cm}f_{\rm D}= \pm 50\,{\rm Hz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5 = {\rm const.}$$

Zusammenhang aller Systemfunktionen

(6)  Wie aus der angegebenen Grafik zu ersehen, treffen die Lösungsalternativen 2 und 3 zu.

• Die Grafik zeigt alle Systemfunktionen.
• Die Fourierkorrespondenzen (grün eingezeichnet) verdeutlichen die Zusammenhänge zwischen diesen Systemfunktionen.

Hinweis:

Vergleichen Sie die zeitvariante Übertragungsfunktion $|\eta_{\rm FZ}(f, \hspace{0.05cm} t)|$ im Bild unten rechts mit der entsprechenden Grafik für Aufgabe 2.4:

• Die jeweils dargestellten Betragsfunktionen unterscheiden sich signifikant, obwohl $|\eta_{\rm VZ}(\tau, t)|$ in beiden Fällen gleich ist.
• In der Aufgabe 2.4 wurde für $\eta_{\rm VZ}(\tau = 1 \ {\rm µ s}, t)$ implizit ein Cosinus vorausgesetzt, hier eine Minus–Cosinusfunktion.
• Die (nicht explizit) angegebene Verzögerungs–Dopplerfunktion für die Aufgabe 2.4 lautete:

$$\eta_{\rm VD}(\tau, f_{\rm D}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2}} \cdot \delta (\tau) \cdot \delta (f_{\rm D} - 100\,{\rm Hz})+$$

$$\hspace{2cm}+\hspace{0.22cm}\frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} - 50\,{\rm Hz})+$$

$$\hspace{2cm}+\hspace{0.22cm} \frac{1}{2} \cdot \delta (\tau- 1\,{\rm \mu s}) \cdot \delta (f_{\rm D} + 50\,{\rm Hz}) \hspace{0.05cm}.$$

• Ein Vergleich mit der Gleichung auf der Angabenseite zeigt, dass sich nur die Vorzeichen der Diracs bei $\tau = 1 \ \rm µ s$ geändert haben.