Abtastung analoger Signale und Signalrekonstruktion

Programmbeschreibung

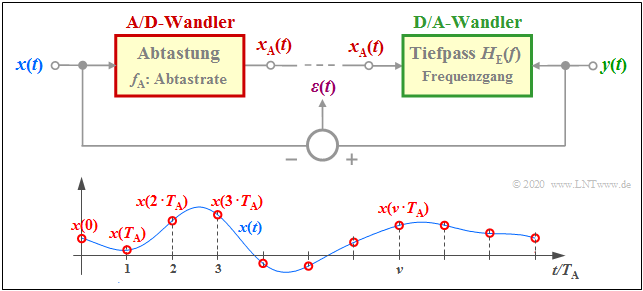
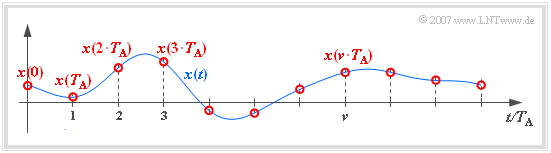
Das Applet behandelt die Systemkomponenten „Abtastung” und „Signalrekonstruktion”, zwei Komponenten, die zum Beispiel für das Verständnis der Pulscodemodulation $({\rm PCM})$ von großer Wichtigkeit sind. Die obere Grafik zeigt das für dieses Applet zugrundeliegende Modell. Darunter gezeichnet sind die Abtastwerte $x(\nu \cdot T_{\rm A})$ des zeitkontinuierlichen Signals $x(t)$ . Die (unendliche) Summe über alle diese Abtastwerte bezeichnen wir als das abgetastete Signal $x_{\rm A}(t)$ .

Oben: Zugrundeliegendes Modell für Abtastung und Signalrekonstruktion
Unten: Beispiel zur Zeitdiskretisierung des zeitkontinuierlichen Signals

$x(t)$

Beim Sender wird aus dem zeitkontinuierlichen Quellensignal $x(t)$ das zeitdiskrete (abgetastete) Signal $x_{\rm A}(t)$ gewonnen. Man nennt diesen Vorgang Abtastung oder A/D–Wandlung.
Der entsprechende Programmparameter für den Sender ist die Abtastrate $f_{\rm A}= 1/T_{\rm A}$ . In der unteren Grafik ist der Abtastabstand $T_{\rm A}$ eingezeichnet.
Beim Empfänger wird aus dem zeitdiskreten Empfangssignal $y_{\rm A}(t)$ das zeitkontinuierliche Sinkensignal $y(t)$ erzeugt ⇒ Signalrekonstruktion oder D/A–Wandlung entsprechend dem Empfänger–Frequenzgang $H_{\rm E}(f)$ .

Das Applet berücksichtigt nicht die PCM–Blöcke „Quantisierung”, „Codierung / Decodierung” und der Digitale Übertragungskanal ist als ideal angenommen.

Daraus ergeben sich folgende Konsequenzen:

Im Programm ist vereinfachend $y_{\rm A}(t) = x_{\rm A}(t)$ gesetzt.
Bei geeigneten Systemparametern ist somit auch das Fehlersignal $\varepsilon(t) = y(t)-x(t)\equiv 0$ möglich.

Empfänger–Frequenzgang

$H_{\rm E}(f)$

Das Abtasttheorem und die Signalrekonstruktion lassen sich im Frequenzbereich besser erklären. Im Programm werden deshalb auch alle Spektralfunktionen angezeigt;

$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t)$ , $X_{\rm A}(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x_{\rm A}(t)$ , $Y(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ y(t)$ , $E(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ \varepsilon(t).$

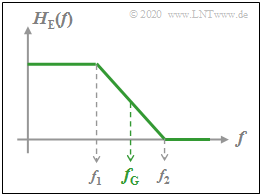
Parameter für den Empfänger–Frequenzgang $H_{\rm E}(f)$ sind die Grenzfrequenz und der Rolloff–Faktor (siehe untere Grafik):

$f_{\rm G} = \frac{f_2 +f_1}{2},\hspace{1cm}r = \frac{f_2 -f_1}{f_2 +f_1}.$

Hinweise:

(1) Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen.

(2) Für die ausgegebenen Leistungen gilt mit der jeweiligen Periodendauer $T_0$ :

$P_x = \frac{1}{T_0} \cdot \int_0^{T_0} x^2(t)\ {\rm d}t,\hspace{0.8cm}P_\varepsilon = \frac{1}{T_0} \cdot \int_0^{T_0} \varepsilon^2(t).$

(3) Die Signalleistung $P_x$ und die Verzerrungsleistung $P_\varepsilon$ werden ebenfalls normiert ausgegeben, was implizit den Bezugswiderstand $R = 1\, \rm \Omega$ voraussetzt.

(4) Daraus kann der Signal–Verzerrungs–Abstand $10 \cdot \lg \ (P_x/P_\varepsilon)$ berechnet werden.

Theoretischer Hintergrund

Beschreibung der Abtastung im Zeitbereich

Zur Zeitdiskretisierung des zeitkontinuierlichen Signals

$x(t)$

Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur:

Das zeitkontinuierliche Signal sei $x(t)$ .
Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$ .
Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) \equiv 0$ .
Die Laufvariable $\nu$ sei ganzzahlig: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\}$ .
Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$ :

$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$

Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$ .

Beschreibung der Abtastung mit Diracpuls

Im Folgenden gehen wir von einer geringfügig anderen Beschreibungsform aus. Die folgenden Seiten werden zeigen, dass diese gewöhnungsbedürftigen Gleichungen durchaus zu sinnvollen Ergebnissen führen, wenn man sie konsequent anwendet.

$\text{Definitionen:}$

Unter Abtastung verstehen wir hier die Multiplikation des zeitkontinuierlichen Signals $x(t)$ mit einem Diracpuls:

$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$

Der Diracpuls (im Zeitbereich) besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$ :

$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$

Aufgrund dieser Definition ergeben sich für das abgetastete Signal folgende Eigenschaften:

$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$

Das abgetastete Signal zum betrachteten Zeitpunkt $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$ .
Da $\delta (t)$ zur Zeit $t = 0$ unendlich ist, sind eigentlich alle Signalwerte $x_{\rm A}(\nu \cdot T_{\rm A})$ ebenfalls unendlich groß und auch der oben eingeführte Faktor $K$ .
Zwei Abtastwerte $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ und $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ unterscheiden sich jedoch im gleichen Verhältnis wie die Signalwerte $x(\nu_1 \cdot T_{\rm A})$ und $x(\nu_2 \cdot T_{\rm A})$ .
Die Abtastwerte von $x(t)$ erscheinen in den Impulsgewichten der Diracfunktionen:
Die zusätzliche Multiplikation mit $T_{\rm A}$ ist erforderlich, damit $x(t)$ und $x_{\rm A}(t)$ gleiche Einheit besitzen. Beachten Sie hierbei, dass $\delta (t)$ selbst die Einheit „1/s” aufweist.

Beschreibung der Abtastung im Frequenzbereich

Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des Faltungssatzes. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht:

$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$

Entwickelt man den Diracpuls $p_{\delta}(t)$ (im Zeitbereich) in eine Fourierreihe und transformiert diese unter Anwendung des Verschiebungssatzes in den Frequenzbereich, so ergibt sich mit dem Abstand $f_{\rm A} = 1/T_{\rm A}$ zweier benachbarter Diraclinien im Frequenzbereich folgende Korrespondenz ⇒ Beweis:

$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$

Diracpuls im Zeit- und Frequenzbereich mit

$T_{\rm A} = 50\ {\rm µs}$ und

$f_{\rm A} = 1/T_{\rm A} = 20\ \text{kHz}$

Das Ergebnis besagt:

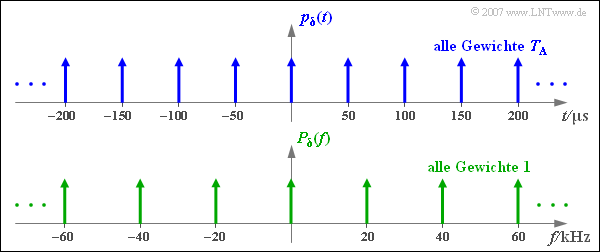
Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$ .
Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$ .
Auch $P_{\delta}(f)$ besteht aus unendlich vielen Diracimpulsen, nun im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$ .
Die Abstände der Diraclinien in Zeit– und Frequenzbereich folgen demnach dem Reziprozitätsgesetz: $T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$

Daraus folgt: Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie:

$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich:

$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

$\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer periodischen Fortsetzung von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$ .

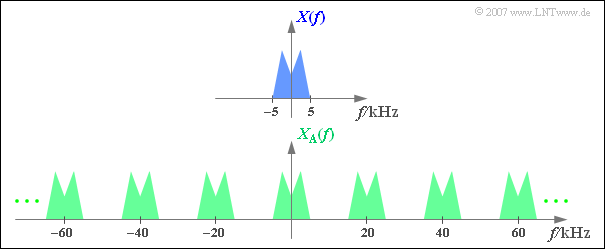
Spektrum des abgetasteten Signals

$\text{Beispiel 1:}$ Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$ , das Frequenzen bis $5 \text{ kHz}$ beinhaltet.

Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$ , also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$ .

Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile.
Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.

Signalrekonstruktion

Gemeinsames Modell von „Signalabtastung” und „Signalrekonstruktion”

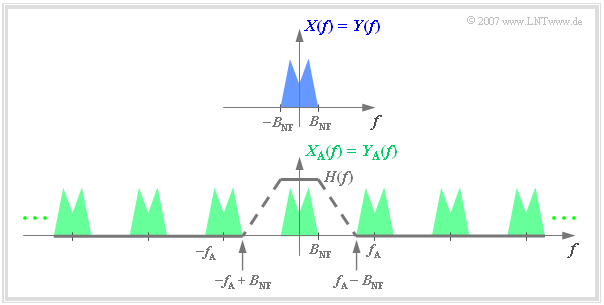
Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden. Betrachten wir zum Beispiel das folgende System:

Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet.
Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor.
Die Frage ist nun, wie der Block Signalrekonstruktion zu gestalten ist, damit auch $y(t) = x(t)$ gilt.

Frequenzbereichsdarstellung der „Signalrekonstruktion”

Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet:

Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch ein Tiefpass Filter mit dem Frequenzgang $H_{\rm E}(f)$ , der

die tiefen Frequenzen unverfälscht durchlässt:

$H_{\rm E}(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$

die hohen Frequenzen vollständig unterdrückt:

$H_{\rm E}(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$

Weiter ist aus der nebenstehenden Grafik zu erkennen: Solange die beiden oben genannten Bedingungen erfüllt sind, kann $H_{\rm E}(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann,

beispielsweise linear abfallend (gestrichelter Verlauf)
oder auch rechteckförmig,

Das Abtasttheorem

Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde.

Aus der obigen Grafik erkennt man, dass folgende Bedingung erfüllt sein muss: $f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$

$\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ nur Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$ , so kann dieses aus seinem abgetasteten Signal $x_{\rm A}(t)$ nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist:

$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$

Für den Abstand zweier Abtastwerte muss demnach gelten:

$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$

Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen,

so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten
ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden.

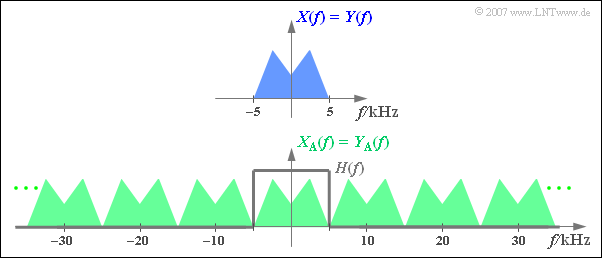
$\text{Beispiel 2:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$ .

Abtasttheorem im Frequenzbereich

Zusätzlich eingezeichnet ist der Frequenzgang $H_{\rm E}(f)$ des tiefpassartigen Empfangsfilters zur Signalrekonstruktion, dessen Grenzfrequenz exakt $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss.

Mit jedem anderen $f_{\rm G}$ –Wert ergäbe sich $Y(f) \neq X(f)$ .
Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$ –Anteile.
Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$ .

Wäre am Sender die Abtastung mit einer Abtastrate $f_{\rm A} < 10\ \text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \ {\rm µ s}$ , so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.

Versuchsdurchführung

Wählen Sie zunächst die Nummer (1, ... , ?) der zu bearbeitenden Aufgabe.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen. Auch die ausgegebenen Leistungen sind normierte Größen.

(1) Für das Quellensignal gelte $x(t) = A \cdot \cos (2\pi \cdot f_0 \cdot t -\varphi)$ mit $f_0 = \text{4 kHz}$ . Abtastung mit $f_{\rm A} = \text{10 kHz}$ . Rechteck–Tiefpass; Grenzfrequenz: $f_{\rm G} = \text{5 kHz}$ .
Interpretieren Sie die ausgegebenen Grafiken und bewerten Sie die vorliegende Signalrekonstruktion für alle erlaubten Parameterwerte von $A$ und $\varphi$ .

Das Spektrum $X(f)$ besteht aus zwei Diraclinien bei $\pm \text{4 kHz}$ , jeweils mit Impulsgewicht $0.5$ .
Durch die periodische Fortsetzung hat $X_{\rm A}(f)$ Linien gleicher Höhe bei $\pm \text{4 kHz}$ , $\pm \text{6 kHz}$ , $\pm \text{14 kHz}$ , $\pm \text{16 kHz}$ , $\pm \text{24 kHz}$ , $\pm \text{26 kHz}$ , usw.
Der Rechteck–Tiefpass mit der Grenzfrequenz $f_{\rm G} = \text{5 kHz}$ entfernt alle Linien bis auf die beiden bei $\pm \text{4 kHz}$ ⇒ $Y(f) =X(f)$ ⇒ $y(t) =x(t)$ ⇒ $\varepsilon \equiv 0$ .
Die Signalrekonstruktion funktioniert hier und zwar für alle Amplituden $A$ und beliebige Phasen $\varphi$ .

Carolin: Bitte Kreise im Imaginärteil von $X_A$ bei der Höhe 0 einzeichnen, wenn der Imaginärteil zwar 0 ist, der Betrag aber größer als 0 (gültig für das Cosinussignal. Das gleiche beim Realteil von $X_A$ . Das betrifft das Sinussignal.

(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$ . Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.

Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$ .

(3) Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?

Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$ , $\varphi_2(t) = s_2(t)$ , $\varphi_3(t) = s_3(t)$ .

(4) Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.

Es gilt $s_3(t) = s_1(t)/4 - s_2(t)/2$ und $s_4(t) = -s_1(t) - s_2(t)$ . Das heißt: $s_3(t)$ und $s_4(t)$ liefern keine neuen Basisfunktionen.

(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$ .

Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$ .
Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).

(6) Welches Ergebnis liefern die vier Signale gemäß der Einstellung $\rm F$ ?

Die die Signale $s_1(t)$ , ... , $s_4(t)$ basieren alle auf einer einzigen Basisfunktion $\varphi_1(t)$ , die formgleich mit $s_1(t)$ ist. Es gilt $N=1$ .
Die vektoriellen Repräsentanten der Signale $s_1(t)$ , ... , $s_4(t)$ sind $\pm 0.866$ und $\pm 1.732$ . Sie liegen alle auf einer Linie.

(7) Es gilt nun die „M–ASK / BPSK”–Einstellung $\rm G$ . Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen.

Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm A$ .
Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor $\sqrt{2}$ aus.
Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (-1.021, \hspace{0.15cm} -0.289, \hspace{0.15cm} +0.500)$ anstelle von $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$ .
Bei der Einstellung $\rm H$ sind gegenüber $\rm G$ alle Amplituden verdoppelt. Somit ergibt sich hier wieder $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$ .

(8) Es gelte die „M–ASK / BPSK”–Einstellung $\rm I$ . Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.

Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm C$ , aber nun mit nur halb so großen Energien.
Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$ .

(9) Wählen Sie die Einstellungen $M=4 \text{, nach Spalt–TP, }T_{\rm E}/T = 1$ , $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ und $12 \ {\rm dB}$ . Interpretieren Sie die Ergebnisse.

Es gibt nun drei Augenöffnungen. Gegenüber (5) ist also $ö_{\rm norm}$ um den Faktor $3$ kleiner, $\sigma_{\rm norm}$ dagegen nur um etwa den Faktor $\sqrt{5/9)} \approx 0.75$ .
Für $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ ergibt sich nun die Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2.27\%$ und für $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ nur mehr $0.59\%$ .

(10) Für die restlichen Aufgaben gelte stets $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ . Betrachten Sie das Augendiagramm für $M=4 \text{, CRO–Nyquist, }r_f = 0.5$ .

In $d_{\rm S}(t)$ müssen alle „Fünf–Symbol–Kombinationen” enthalten sein ⇒ mindestens $4^5 = 1024$ Teilstücke ⇒ maximal $1024$ unterscheidbare Linien.
Alle $1024$ Augenlinien gehen bei $t=0$ durch nur vier Punkte: $ö_{\rm norm}= 0.333$ . $\sigma_{\rm norm} = 0.143$ ist etwas größer als in (9) ⇒ ebenso $p_{\rm U} \approx 1\%$ .

(11) Wählen Sie die Einstellungen $M=4 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ und variieren Sie $f_{\rm G}/R_{\rm B}$ . Interpretieren Sie die Ergebnisse.

$f_{\rm G}/R_{\rm B}=0.48$ führt zur minimalen Fehlerwahrscheinlichkeit $p_{\rm U} \approx 0.21\%$ . Kompromiss zwischen $ö_{\rm norm}= 0.312$ und $\sigma_{\rm norm}= 0.109$ .
Bei zu kleiner Grenzfrequenz dominieren die Impulsinterferenzen. Beispiel: $f_{\rm G}/R_{\rm B}= 0.3$ : $ö_{\rm norm}= 0.157;$ $\sigma_{\rm norm}= 0.086$ ⇒ $p_{\rm U} \approx 3.5\%$ .
Bei zu großer Grenzfrequenz dominiert das Rauschen. Beispiel: $f_{\rm G}/R_{\rm B}= 1.0$ : $ö_{\rm norm}= 0.333;$ $\sigma_{\rm norm}= 0.157$ ⇒ $p_{\rm U} \approx 1.7\%$ .
Aus dem Vergleich mit (9) erkennt man: Bei Quaternärcodierung ist es günstiger, Impulsinterferenzen zuzulassen.

(12) Welche Unterschiede zeigt das Auge für $M=3 \text{ (AMI-Code), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ gegenüber dem vergleichbaren Binärsystem? Interpretation.

Der Detektionsgrundimpuls $g_d(t)$ ist in beiden Fällen gleich. Die Abtastwerte sind jeweils $g_0 = 0.771, \ g_1 = 0.114$ .
Beim AMI–Code gibt es zwei Augenöffnungen mit je $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$ . Beim Binärcode: $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$ .
Die AMI–Folge besteht zu 50% aus Nullen. Die Symbole $+1$ und $-1$ wechseln sich ab ⇒ es gibt keine lange $+1$ –Folge und keine lange $-1$ –Folge.
Darin liegt der einzige Vorteil des AMI–Codes: Dieser kann auch bei einem gleichsignalfreien Kanal ⇒ $H_{\rm K}(f= 0)=0$ angewendet werden.

(13) Gleiche Einstellung wie in (12), zudem $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ . Analysieren Sie die Fehlerwahrscheinlichkeit des AMI–Codes.

Trotz kleinerem $\sigma_{\rm norm} = 0.103$ hat der AMI–Code eine höhere Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2\%$ als der Binärcode: $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
Für $f_{\rm G}/R_{\rm B}<0.34$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ ⇒ $p_{\rm U} =50\%$ . Beim Binärcode: Für $f_{\rm G}/R_{\rm B}>0.34$ ist das Auge geöffnet.

(14) Welche Unterschiede zeigt das Auge für $M=3 \text{ (Duobinärcode), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.30$ gegenüber dem vergleichbaren Binärsystem?

Redundanzfreier Binärcode: $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\%$ Duobinärcode: $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\%$ .
Insbesondere bei kleinem $f_{\rm G}/R_{\rm B}$ liefert der Duobinärcode gute Ergebnisse, da die Übergänge von $+1$ nach $-1$ (und umgekehrt) im Auge fehlen.
Selbst mit $f_{\rm G}/R_{\rm B}=0.2$ ist das Auge noch geöffnet. Im Gegensatz zum AMI–Code ist aber „Duobinär” bei gleichsignalfreiem Kanal nicht anwendbar.

Zur Handhabung des Applets

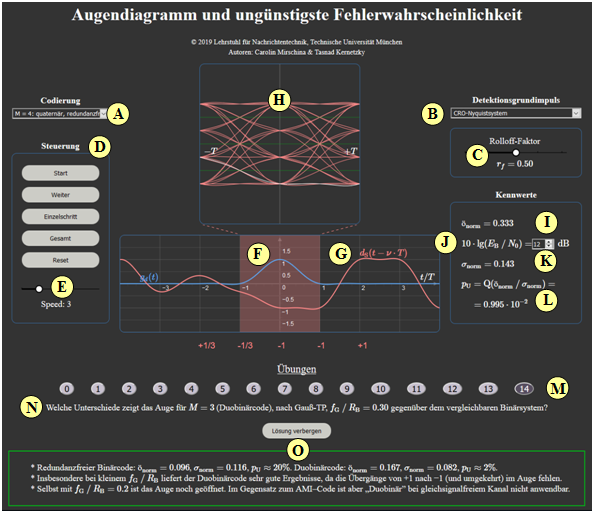
(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)

(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}

(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)

(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)

(E) Geschwindigkeit der Augendiagrammdarstellung

(F) Darstellung: Detektionsgrundimpuls $g_d(t)$

(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$

(H) Darstellung: Augendiagramm im Bereich $\pm T$

( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)

(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)

(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)

(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)

(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl

(N) Bereich für die Versuchsdurchführung: Aufgabenstellung

(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2008 von Thomas Großer im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab