Zur Verdeutlichung digitaler Filter

Theoretischer Hintergrund

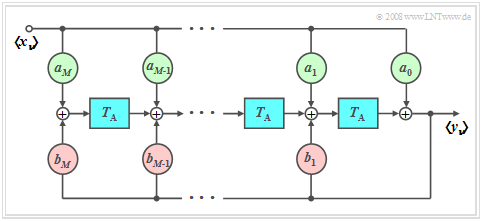
Allgemeines Blockschaltbild

Jedes Signal $x(t)$ kann an einem Rechner nur durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt werden, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht.

Blockschaltbild eines digitalen (IIR–) Filters $M$–Ordnung

Der zeitliche Abstand $T_{\rm A}$ zwischen zwei Abtastwerten ist dabei durch das Abtasttheorem nach oben begrenzt.
Wir beschränken uns hier auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ für $ν \le 0$.

Um den Einfluss eines linearen Filters mit Frequenzgang $H(f)$ auf das zeitdiskrete Eingangssignal $〈x_ν〉$ zu erfassen, bietet es sich an, auch das Filter zeitdiskret zu beschreiben. Im Zeitbereich geschieht das mit der zeitdiskreten Impulsantwort $〈h_ν〉$.
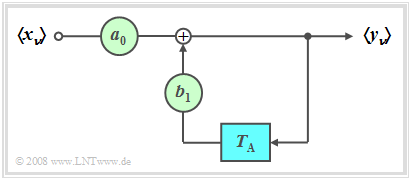
Rechts sehen Sie das entsprechende Blockschaltbild. Für die Abtastwerte des Ausgangssignals $〈y_ν〉$ gilt somit:

$$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu } \cdot x_{\nu - \mu } + \sum\limits_{\mu = 1}^M {b_\mu } \cdot y_{\nu - \mu } .$$

Hierzu ist Folgendes zu bemerken:

Der Index $\nu$ bezieht sich auf Folgen, zum Beispiel Eingang $〈x_ν〉$ und Ausgang $〈y_ν〉$.
Den Index $\mu$ verwenden wir dagegen für die Kennzeichnung der $a$– und $b$–Filterkoeffizienten.
Die erste Summe beschreibt die Abhängigkeit des aktuellen Ausgangs $y_ν$ vom aktuellen Eingang $x_ν$ und von den $M$ vorherigen Eingangswerten $x_{ν-1}$, ... , $x_{ν-M}.$
Die zweite Summe kennzeichnet die Beeinflussung von $y_ν$ durch die vorherigen Werte $y_{ν-1}$, ... , $y_{ν-M}$ am Filterausgang. Sie gibt den rekursiven Teil des Filters an.
Den ganzzahligen Parameter $M$ bezeichnet man als die Ordnung des digitalen Filters. Im Programm ist dieser Wert auf $M\le 2$ begrenzt.

$\text{Definitionen:}$

(1) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Impulsantwort $〈h_ν〉$, wenn am Eingang die „zeitdiskrete Diracfunktion” anliegt:

$$〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉 .$$

(2) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Sprungantwort $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt:

$$〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 .$$

(3) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Recheckantwort $〈\rho_ν^{(2, 4)}〉$, wenn am Eingang die „zeitdiskrete Rechteckfunktion” anliegt:

$$〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 .$$

In Hochkommata angegeben sind hier der Beginn der Einsen $(2)$ und die Stelle der letzten Eins $(4)$.

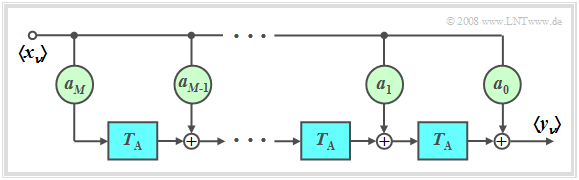
Nichtrekursives Filter ⇒ FIR–Filter

Nichtrekursives digitales Filter $($FIR–Filter$)$ $M$–Ordnung

$\text{Definition:}$ Sind alle Rückführungskoeffizienten $b_{\mu} = 0$, so spricht von einem nichtrekursiven Filter. Insbesondere in der englischsprachigen Literatur ist hierfür auch die Bezeichnung FIR Filter (Finite Impulse Response) gebräuchlich.

Für die Ordnung $M$ gilt:

Der Ausgangswert $y_ν$ hängt nur vom aktuellen und den $M$ vorherigen Eingangswerten ab:

$$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu \cdot x_{\mu - \nu } } .$$

Zeitdikrete Impulsantwort mit $〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉$:

$$〈h_\mu〉= 〈a_0,\ a_1,\ \text{...},\ a_M〉 .$$

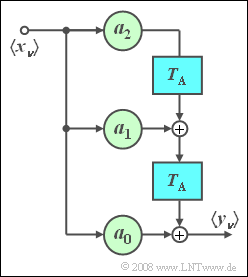
$\text{Beispiel 1:}$ Ein Zweiwegekanal, bei dem

das Signal auf dem Hauptpfad gegenüber dem Eingangssignal ungedämpft, aber um $2\ \rm µ s$ verzögert ankommt, und
in $4\ \rm µ s$ Abstand – also absolut zur Zeit $t = 6\ \rm µ s$ – ein Echo mit halber Amplitude nachfolgt,

kann durch ein nichtrekursives Filter entsprechend obiger Skizze nachgebildet werden, wobei folgende Parameterwerte einzustellen sind:

$$M = 3,\quad T_{\rm A} = 2\;{\rm{µ s} },\quad a_{\rm 0} = 0,\quad a_{\rm 1} = 1, \quad a_{\rm 2} = 0, \quad a_{\rm 3} = 0.5.$$

$\text{Beispiel 2:}$ Betrachtet wird ein nichtrekursives Filter mit den Filterkoeffizienten $a_0 = 1,\hspace{0.5cm} a_1 = 2,\hspace{0.5cm} a_2 = 1.$

Nichtrekursives Filter

(1) Die herkömmliche Impulsantwort lautet: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$
⇒ Zeitdiskrete Impulsantwort: $〈h_\mu〉= 〈1,\ 2,\ 1〉 .$

(2) Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$. Durch Anwendung des Verschiebungssatzes:

$$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }\cdot }f \cdot T_{\rm A} } )} \big ] \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm A} }\hspace{0.5cm}\Rightarrow \hspace{0.5cm}H(f = 0) = 4.$$

(3) Daraus folgt: Die zeitdiskrete Sprungantwort $〈\sigma_ν〉$ tendiert für große $\nu$ gegen $4$.

(4) Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;0,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt

$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;2,\;1,\;0,\;1,\;2,\;1,\;0,\;0,\;0,\;0,\; \text{...} \;} \right\rangle. $$

(5) Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;1,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt

$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;3,\;1,\;0,\;0,\;0,\;0,\;0,\;0,\;0,\; \text{...} \;} \right\rangle. $$

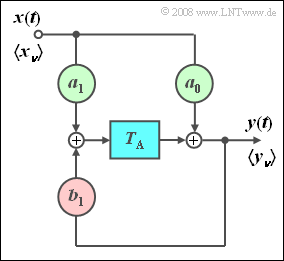
Rekursives Filter ⇒ IIR–Filter

Rekursives Filter erster Ordnung

$\text{Definition:}$

Ist zumindest einer der Rückführungskoeffizienten $b_{\mu} \ne 0$, so spricht von einem rekursiven Filter (siehe rechte Grafik). Insbesondere in der englischsprachigen Literatur ist hierfür auch die Bezeichnung IIR Filter (Infinite Impulse Response) gebräuchlich. Dieses Filter wird in der Verrsuchsdurchführung ausführlich behandelt.

Sind zusätzlich alle Vorwärtskoeffizienten identisch $a_\mu = 0$ mit Ausnahme von $a_0$, so liegt ein rein rekursives Filter vor (siehe linke Grafik).

Rein rekursives Filter erster Ordnung

Im Folgenden beschränken wir uns auf den Sonderfall „Rein rekursives Filter erster Ordnung”. Dieses Filter weist folgende Eigenschaften auf:

Der Ausgangswert $y_ν$ hängt (indirekt) von unendlich vielen Eingangswerten ab:

$$y_\nu = \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot x_{\nu - \mu } .}$$

Dies zeigt die folgende Rechung:

$$y_\nu = a_0 \cdot x_\nu + b_1 \cdot y_{\nu - 1} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + {b_1} ^2 \cdot y_{\nu - 2} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + a_0 \cdot {b_1} ^2 \cdot x_{\nu - 2} + {b_1} ^3 \cdot y_{\nu - 3} = \text{...}. $$

Die zeitdiskrete Impulsantwort ist definitionsgemäß der Ausgangsfolge, wenn am Eingang eine einzelne „Eins” bei $t =0$ anliegt.

$$h(t)= \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉= 〈\hspace{0.05cm}a_0, \ a_0\cdot {b_1}, \ a_0\cdot {b_1}^2 \ \text{...} \hspace{0.05cm}〉.$$

$\text{Fazit:}$ Bei einem rekursiven Filter reicht die (zeitdiskrete) Impulsantwort schon mit $M = 1$ bis ins Unendliche:

Aus Stabilitätsgründen muss $b_1 < 1$ gelten.
Bei $b_1 = 1$ würde sich die Impulsantwort $h(t)$ bis ins Unendliche erstrecken und bei $b_1 > 1$ würde $h(t)$ sogar bis ins Unendliche anklingen.
Bei einem solchen rekursiven Filter erster Ordnung ist jede einzelne Diraclinie genau um den Faktor $b_1$ kleiner als die vorherige Diraclinie:

$$h_{\mu} = h(\mu \cdot T_{\rm A}) = {b_1} \cdot h_{\mu -1}.$$

rechts

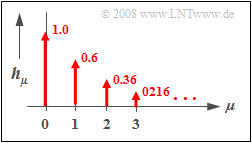
$\text{Beispiel 3:}$ Die nebenstehende Grafik zeigt die zeitdiskrete Impulsantwort $〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉$ eines rekursiven Filters erster Ordnung mit den Parametern $a_0 = 1$ und $b_1 = 0.6$.

Der Verlauf ist exponentiell abfallend und erstreckt sich bis ins Unendliche.
Das Verhältnis der Gewichte zweier aufeinander folgender Diracs ist jeweils $b_1 = 0.6$.

Versuchsdurchführung

Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.

In den folgenden Aufgabenbeschreibungen werden folgende Kurzbezeichnungen verwendet:

Rot: Regressionsgerade $R_{Y \to X}$ (im Applet rot gezeichnet),
Blau: Regressionsgerade $R_{X \to Y}$ (im Applet blau gezeichnet).

(1) Mit welcher Parametereinstellung sind die beiden Regressionsgeraden $R_{Y \to X}$ und $R_{X \to Y}$ deckungsgleich?

Es ist offensichtlich, dass gleiche Regressionsgeraden nur möglich sind, wenn diese unter dem Winkel $45^\circ$ verlaufen ⇒ „Winkelhalbierende”.
Da die fest vorgegebenen Punkte $3$ und $4$ auf der Winkelhalbierenden liegen, muss dies auch für die Punkte $1$ und $2$ gelten ⇒ $y_1 = x_1$.
Dies gilt für alle Parametereinstellungen $y_1 = x_1$ und auch für alle $p_1$ im erlaubten Bereich von $0$ bis $0.5$.

(2) Nun gelte $x_1 = 0.5,\ y_1 = 0,\ p_1 = 0.3$ Interpretieren Sie die Ergebnisse. Aktivieren Sie hierzu die Hilfsgerade.

Diese Einstellung stimmt mit den Voraussetzungen zu $\text{Beispiel 1}$ und $\text{Beispiel 2}$ überein. Insbesondere gilt $ \theta_{X \to Y}= 45^\circ$ und $ \theta_{Y \to X}\approx 36^\circ$.
Durch Variation des Winkels $ \theta_{\rm HG}$ erkennt man, dass für $ \theta_{\rm HG}= 45^\circ$ die Kenngröße ${\rm MQA}_X =0.15$ tatsächlich den kleinsten Wert annimmt.
Ebenso ergibt sich der kleinstmögliche Abstand ${\rm MQA}_Y =0.109$ in $y$–Richtung für $ \theta_{\rm HG}= 36^\circ$, also entsprechend der Geraden $R_{Y \to X}$.

(3) Es gelten zunächst weiter die Einstellungen von (2). Wie ändern sich die Ergebnisse nach Variation von $p_1$ im erlaubten Bereich $(0\le p_1 \le 0.5)$?

Die blaue Regressionsgerade $ R_{X \to Y}$ verläuft weiter unter dem Winkel $ \theta_{X \to Y}= 45^\circ$ ⇒ es gilt hier $\mu_{XY} =\sigma_Y^2$, und zwar unabhängig von $p_1 < 0.5$.
Im Grenzfall $p_1 = 0.5$ ist wegen $\sigma_Y =0$ die blaue Regressionsgerade undefiniert. Es handelt sich nurmehr um eine 1D–Zufallsgröße $X$.
Mit $p_1=0$ sind nur die äußeren Punkte $3$ und $4$ wirksam ⇒ $ \theta_{Y \to X}= \theta_{X \to Y}= 45^\circ$, mit $p_1=0.5$ nur die inneren Punkte ⇒ $ \theta_{Y \to X}= 0^\circ$.
Dazwischen wird $ R_{Y \to X}$ kontinuierlich flacher. Sind alle Punkte gleichwahrscheinlich $(p_1=0.25)$, dann ist $\theta_{Y \to X}\approx 38.7^\circ$.

(4) Nun gelte $x_1 = 0,\ y_1 = 0.5,\ p_1 = 0.3$. Variieren Sie $0\le p_1 < 0.5$ und interpretieren Sie die Ergebnisse. $(p_1 = 0.5$ sollte man ausschließen$)$.

Wegen $\sigma_X \le \sigma_Y$ liegt weiterhin die blaue Gerade nie unterhalb der roten, die für alle $p_1 \ne 0.5$ die Winkelhalbierende ist ⇒ $ \theta_{Y \to X}\approx 45^\circ$.
Der Winkel der blauen Regressionsgerade wächst von $ \theta_{X \to Y}= 45^\circ \ (p_1 = 0)$ bis $ \theta_{X \to Y} \to 90^\circ \ (p_1 \to 0.5)$ kontinuierlich an.

(5) Beginnen Sie mit $x_1 = 0.8,\ y_1 = -0.8,\ p_1 = 0.25$ und vergrößern Sie $y_1$ bis zum Endwert $y_1 = +0.8$. Interpretieren Sie die Ergebnisse.

Für $y_1 =-0.8$ ist $ \theta_{X \to Y}= 77.6^\circ$ und $ \theta_{Y \to X}= 12.4^\circ$. Mit steigendem $y_1$ verläuft $ R_{X \to Y}$ (blau) flacher und $R_{Y \to X}$ (rot) steiler.
Im Endpunkt $(y_1 = +0.8)$ verlaufen die beiden Regressionsgeraden deckungsgleich unter dem Winkel $ \theta_{X \to Y}= \theta_{Y \to X}= 45^\circ$.

(6) Abschließend gelte $x_1 = +1,\ y_1 = -1$. Variieren Sie $p_1$ im gesamten zulässigen Bereich $0\le p_1 \le 0.5$. Wann sind $X$ und $Y$ unkorreliert?

Für $p_1 = 0$ gilt $ \theta_{X \to Y}=\theta_{Y \to X}= 45^\circ.$ Dann dreht die blaue Gerade entgegen dem Uhrzeigersinn, die rote Gerade im Uhrzeigersinn.
Für $p_1 = 0.25$ sind die Winkel $ \theta_{X \to Y}=90^\circ, \ \theta_{Y \to X}= 0^\circ.$ Diese Momentaufnahme beschreibt unkorrelierte Zufallsgrößen ⇒ $\mu_{XY}=0$.
Anschließend drehen beide Geraden weiter in gleicher Richtung. Für $p_1 = 0.5$ gilt schließlich: $ \theta_{X \to Y}=135^\circ= -45^\circ, \ \theta_{Y \to X}= -45^\circ.$

Zur Handhabung des Applets

(A) Vorauswahl für blauen Parametersatz

(B) Parametereingabe $I$ und $p$ per Slider

(C) Vorauswahl für roten Parametersatz

(D) Parametereingabe $\lambda$ per Slider

(E) Graphische Darstellung der Verteilungen

(F) Momentenausgabe für blauen Parametersatz

(G) Momentenausgabe für roten Parametersatz

(H) Variation der grafischen Darstellung

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$

(J) Bereich für die Versuchsdurchführung

Andere Möglichkeiten zur Variation der grafischen Darstellung:

Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2020 wurde das Programm von Veronika Hofmann (Ingenieurspraxis Mathematik, Betreuer: Benedikt Leible und Tasnád Kernetzky ) unter „HTML5” neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab