Exercise 1.10: BPSK Baseband Model

• Return to book

Unsymmetrischer Kanalfrequenzgang

Wir betrachten in dieser Aufgabe ein BPSK–System mit kohärenter Demodulation, das heißt, es gilt

$$s(t) \ = \ z(t) \cdot q(t),$$

$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$

Die hier gewählten Bezeichnungen lehnen sich an das  Blockschaltbild  im Theorieteil an.

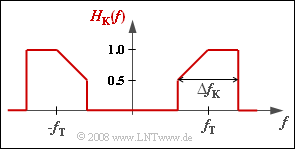
Der Einfluss eines Kanalfrequenzgangs  $H_{\rm K}(f)$  lässt sich in einfacher Weise berücksichtigen, wenn man diesen zusammen mit Modulator und Demodulator durch einen gemeinsamen Basisbandfrequenzgang beschreibt:

$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$

• Damit werden Modulator und Demodulator quasi gegeneinander gekürzt, und
• der Bandpasskanal  $H_{\rm K}(f)$  wird in den Tiefpassbereich transformiert.

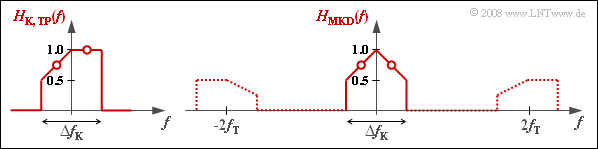
Die resultierende Übertragungsfunktion  $H_{\rm MKD}(f)$  sollte man nicht mit der Tiefpass–Übertragungsfunktion  $H_{\rm K, \, TP}(f)$  gemäß der Beschreibung im Kapitel  Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion  des Buches „Signaldarstellung” verwechseln, die sich aus  $H_{\rm K}(f)$  durch Abschneiden der Anteile bei negativen Frequenzen sowie einer Frequenzverschiebung um  $f_{\rm T}$  nach links ergibt.

Bei Frequenzgängen muss im Gegensatz zu Spektralfunktionen auf die Verdoppelung der Anteile bei positiven Frequenzen verzichtet werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Lineare digitale Modulation – Kohärente Demodulation.
• Bezug genommen wird insbesondere auf die Seite  Basisbandmodell für ASK und BPSK.

Fragebogen

1

Welche Aussagen gelten für die äquivalente Tiefpassfunktion  $H_{\rm K, \, TP}(f)$ ?

	Es gilt  $H_{\rm K, \, TP}(f=0)= 2$.
	Es gilt  $H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$.
	Es gilt  $H_{\rm K, \, TP}(f = –\Delta f_{\rm K}/4) = 0.75$.
	Die dazugehörige Zeitfunktion  $h_{\rm K, \, TP}(t)$  ist komplex.

2

Welche Aussagen gelten für den Frequenzgang  $H_{\rm MKD}(f)$ ?

	Es gilt  $H_{\rm MKD}(f=0)= 2$.
	Es gilt  $H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$.
	Es gilt  $H_{\rm MKD}(f = –\Delta f_{\rm K}/4) = 0.75$.
	Die dazugehörige Zeitfunktion  $h_{\rm MKD}(t)$  ist komplex.

3

Berechnen Sie die Zeitfunktion  $h_{\rm MKD}(t)$. Geben Sie den Wert bei  $t = 0$  an.

$h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $

4

Welche der folgenden Aussagen treffen zu?

	$h_{\rm MKD}(t)$  hat äquidistante Nulldurchgänge im Abstand  $1/\Delta f_{\rm K}$.
	$h_{\rm MKD}(t)$  hat äquidistante Nulldurchgänge im Abstand  $2/\Delta f_{\rm K}$.

Musterlösung

Solution

(1)  Richtig sind die die Aussagen 2, 3 und 4:

• $H_{\rm K,TP}(f)$ ergibt sich aus $H_{\rm K}(f)$ durch Abschneiden der negativen Frequenzanteile sowie Verschieben um $f_{\rm T}$ nach links.
• Bei Frequenzgängen wird – im Gegensatz zu Spektren – auf das Verdoppeln der Anteile bei positiven Frequenzen verzichtet. Deshalb:

$$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$

• Wegen der reellen und unsymmetrischen Spektralfunktionen $H_{\rm K,\hspace{0.04cm}TP}(f)$ ist die zugehörige Zeitfunktion (Fourierrücktransformierte) $h_{\rm K,\hspace{0.04cm}TP}(t)$ nach dem Zuordnungssatz komplex.

Tiefpassfunktionen für $H_{\rm K}(f)$

(2)  Hier ist nur der dritte Lösungsvorschlag richtig:

• Die Spektralfunktion $H_{\rm MKD}(f)$ besitzt stets einen geraden Realteil und keinen Imaginärteil. Demzufolge ist $h_{\rm MKD}(t)$ stets reell.
• Hätte $H_{\rm K}(f)$ zusätzlich einen um $f_{\rm T}$ ungeraden Imaginärteil, so würde $H_{\rm MKD}(f)$ einen um $f = 0$ ungeraden Imaginärteil aufweisen. Damit wäre $h_{\rm MKD}(t)$ immer noch eine reelle Funktion.

Die Grafik verdeutlicht die Unterschiede zwischen $H_{\rm K,\hspace{0.04cm}TP}(f)$ und $H_{\rm MKD}(f)$. Die Anteile von $H_{\rm MKD}(f)$ im Bereich um $\pm 2f_{\rm T}$ müssen nicht weiter beachtet werden.

(3)  $H_{\rm MKD}(f)$ setzt sich additiv aus einem Rechteck und einem Dreieck zusammen, jeweils mit Breite $\Delta f_{\rm K}$ und Höhe $0.5$. Daraus folgt:

$$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (\pi \cdot \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi \cdot \frac{\Delta f_{\rm K}}{2} \cdot t)$$

$$\Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$

(4)  Richtig ist der zweite Lösungsvorschlag:

• Die erste si–Funktion besitzt zwar äquidistante Nulldurchgänge im Abstand $1/\Delta f_{\rm K}$.
• Die äquidistanten Nulldurchgänge der gesamten Zeitfunktion $h_{\rm MKD}$ werden aber durch den zweiten Term bestimmt:

$$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (\pi )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi/2) = \frac{\Delta f_{\rm K}}{4},$$

$$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (2\pi )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi) = 0.$$