Contents
Applet Description
The applet is intended to illustrate the „Doppler effect”, named after the Austrian mathematician, physicist and astronomer Christian Andreas Doppler. This predicts the change in the perceived frequency of waves of any kind, which occurs when the source (transmitter) and observer (receiver) move relative to each other. Because of this, the reception frequency $f_{\rm E}$ differs from the transmission frequency $f_{\rm S}$. The Doppler frequency $f_{\rm D}=f_{\rm E}-f_{\rm S}$ is positive if the observer and the source approach each other, otherwise the observer perceives a lower frequency than which was actually transmitted.
The exact equation for the reception frequency $f_{\rm E}$ considering the theory of relativity is:
- $$f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\text{ exact equation}}.$$
- Here is $v$ the relative speed between transmitter and receiver, while $c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light.
- $\alpha$ is the angle between the direction of movement and the connecting line between transmitter and receiver.
- $\varphi$ denotes the angle between the direction of movement and the horizontal in the applet. In general, $\alpha \ne \varphi$.
At realistic speeds $(v/c \ll 1)$ the following approximation is sufficient, ignoring the effects of relativity:
- $$f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\text{ approximation}}\hspace{0.05cm}.$$
For example, in the case of mobile communications, the deviations between $f_{\rm E}$ and $f_{\rm S}$ – the Doppler frequency $f_{\rm D}$ – only a fraction of the transmission frequency.
Theoretical Background
Phenomenological description of the Doppler effect
$\text{Definition:}$ As $\rm Doppler effect$ is the change in the perceived frequency of waves of any kind that occurs when the source (transmitter) and observer (receiver) move relative to each other. This was invented by the Austrian mathematician, physicist and astronomer Christian Andreas Doppler in the middle of the 19th century theoretically predicted and named after him.
The Doppler impact can be described qualitatively as follows:
- If the observer and the source approach each other, the frequency increases from the observer's point of view, regardless of whether the observer is moving or the source or both.
- If the source moves away from the observer or the observer moves away from the source, the observer perceives a lower frequency than was actually transmitted.
$\text{Beispiel 1:}$ We look at the change in pitch of the "Martinhorn" of an ambulance. As long as the vehicle is approaching, the observer hears a higher tone than when the vehicle is stationary. If the ambulance moves away, a lower tone is perceived.
The same effect can be seen in a car race. The faster the cars drive, the clearer the frequency changes and the “sound”.
$\text{Beispiel 2:}$
Some properties of this effect, which is still known from physics lessons, are now to be shown on the basis of screen shots from an earlier version of the present applet, with the dynamic program properties of course being lost.
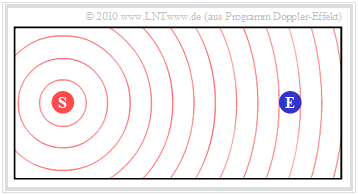
The first graphic shows the initial situation:
- The stationary transmitter $\rm (S)$ emits the constant frequency $f_{\rm S}$.
- The wave propagation is illustrated in the graphic by concentric circles around $\rm (S)$ illustrated.
- The receiver $\rm (E)$ , which is also at rest, receives the frequency $f_{\rm E} = f_{\rm S}$.
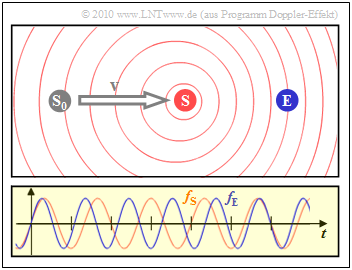
$\text{Beispiel 3:}$ In this snapshot, the transmitter $\rm (S)$ has moved from its starting point $\rm (S_0)$ to the receiver $\rm (E)$ at a constant speed.
- The diagram on the right shows that the frequency $f_{\rm E}$ perceived by the receiver (blue oscillation) is about $20\%$ greater than the frequency $f_{\rm S}$ on the transmitter (red oscillation).
- Due to the movement of the transmitter, the circles are no longer concentric.
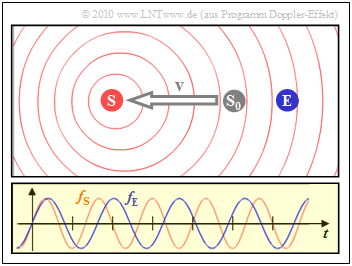
- The left scenario is the result when the sender $\rm (S)$ moves away from the receiver $\rm (E)$:
- Then the reception frequency $f_{\rm E}$(blue oscillation) is about $20\%$ lower than the transmission frequency $f_{\rm S}$.
Doppler frequency as a function of speed and angle of the connecting line
We agree: the frequency $f_{\rm S}$ is sent and the frequency $f_{\rm E}$ is received. The Doppler frequency is the difference $f_{\rm D} = f_{\rm E} - f_{\rm S}$ due to the relative movement between the transmitter (source) and receiver (observer).
- A positive Doppler frequency $(f_{\rm E} > f_{\rm S})$ arises when the transmitter and receiver move (relatively) towards each other.
- A negative Doppler frequency $(f_{\rm E} < f_{\rm S})$ means that the sender and receiver are moving apart (directly or at an angle).
The exact equation for the reception frequency $f_{\rm E} including an angle $\alpha$ between the direction of movement and the connecting line between transmitter and receiver is:
:\[f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\text{ exact equation}}.\]
Here $v$ denotes the relative speed between transmitter and receiver, while $c = 3 \cdot 10^8 \, {\rm m/s}$ indicates the speed of light.
*The graphics in $\text{Beispiel 3}$ apply to the unrealistically high speed $v = c/5 = 60000\, {\rm km/s}$, which lead to the Doppler frequencies $f_{\rm D} = \pm 0.2\cdot f_{\rm S}$.
*In the case of mobile communications, the deviations between $f_{\rm S}$ and $f_{\rm E}$ are usually only a fraction of the transmission frequency. At such realistic velocities $(v \ll c)$ one can start from the following approximation, which does not take into account the effects described by the [https://en.wikipedia.org/wiki/Theory_of_relativity theory of relativity] beschriebenen Effekte unberücksichtigt bleiben:
:\[f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\text{ Näherung}}\hspace{0.05cm}.\]
<div class="greybox">
$\text{Beispiel 4:}$ Wir gehen hier von einem festen Sender aus. Der Empfänger nähert sich dem Sender unter dem Winkel $\alpha = 0$.
Untersucht werden sollen verschiedene Geschwindigkeiten:
* eine unrealistisch große Geschwindigkeit $v_1 = 0.6 \cdot c = 1.8 \cdot 10^8 \ {\rm m/s}$ $\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_1/c = 0.6$,
* die Maximalgeschwindigkeit $v_2 = 3 \ {\rm km/s} \ \ (10800 \ {\rm km/h})$ bei unbemanntem Testflug $\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_2/c = 10^{-5}$,
* etwa die Höchstgeschwindigkeit $v_3 = 30 \ {\rm m/s} = 108 \ \rm km/h$ auf Bundesstraßen $\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_3/c = 10^{-7}$.
'''(1)''' Nach der exakten, relativistischen ersten Gleichung gilt:
:'"`UNIQ-MathJax4-QINU`"'
:'"`UNIQ-MathJax5-QINU`"'
:'"`UNIQ-MathJax6-QINU`"'
:'"`UNIQ-MathJax7-QINU`"'
:'"`UNIQ-MathJax8-QINU`"'
:'"`UNIQ-MathJax9-QINU`"'
:'"`UNIQ-MathJax10-QINU`"'
:'"`UNIQ-MathJax11-QINU`"'
'''(2)''' Dagegen gilt nach der Näherung, also ohne Berücksichtigung der Relativitätstheorie:
:'"`UNIQ-MathJax12-QINU`"'
:'"`UNIQ-MathJax13-QINU`"'
:'"`UNIQ-MathJax14-QINU`"'
:'"`UNIQ-MathJax15-QINU`"'
<div style="clear:both;">
</div>
</div>
<div class="bluebox">
$\text{Fazit:}$
# Für „kleine” Geschwindigkeiten liefert die Näherung bis hin zur Genauigkeit eines Taschenrechners das gleiche Ergebnis wie die relativistische Gleichung.
# Die Zahlenwerte zeigen, dass wir auch die Geschwindigkeit $v_2 = \ 10800 \ {\rm km/h}$ in dieser Hinsicht noch als „klein” bewerten können.
<div style="clear:both;">
</div>
</div>
<div class="greybox">
$\text{Beispiel 5:}$ Es gelten die gleichen Voraussetzungen wie im letzten Beispiel mit dem Unterschied: Nun entfernt sich der Empfänger vom Sender $(\alpha = 180^\circ)$.
'''(1)''' Nach der exakten, relativistischen ersten Gleichung gilt mit ${\rm cos}(\alpha) = -1$:
:'"`UNIQ-MathJax16-QINU`"'
:'"`UNIQ-MathJax17-QINU`"'
:'"`UNIQ-MathJax18-QINU`"'
:'"`UNIQ-MathJax19-QINU`"'
'''(2)''' Dagegen gilt nach der Näherung, also ohne Berücksichtigung der Relativitätstheorie:
:'"`UNIQ-MathJax20-QINU`"'
:'"`UNIQ-MathJax21-QINU`"'
:'"`UNIQ-MathJax22-QINU`"'
<div style="clear:both;">
</div>
</div>
<div class="bluebox">
$\text{Fazit:}$
# Die Empfangsfrequenz $f_{\rm E}$ ist nun kleiner als die Sendefrequenz $f_{\rm S}$ und die Dopplerfrequenz $f_{\rm D}$ ist negativ.
# Bei der Näherung unterscheiden sich die Dopplerfrequenzen für die beiden Bewegungsrichtungen nur im Vorzeichen ⇒ $f_{\rm E} = f_{\rm S} \pm f_{\rm D}$.
# Bei der exakten, relativistischen Gleichung ist diese Symmetrie nicht gegeben.
<div style="clear:both;">
</div>
</div>
<div class="greybox">
$\text{Beispiel 6:}$ Nun betrachten wir die auch für den Mobilfunk realistische Geschwindigkeit $v = 30 \ {\rm m/s} = 108 \ \rm km/h$ ⇒ $v/c=10^{-7}$.
[[File:P_ID2118__Mob_Z_1_4.png|right|frame|Richtungen $\rm (A)$, $\rm (B)$, $\rm (C)$, $\rm (D)$]]
*Damit können wir uns auf die nichtrelativistische Näherung beschränken: $f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot {v}/{c} \cdot \cos(\alpha) \hspace{0.05cm}.$
*Wie in den vorherigen Beispielen sei der Sender fest. Die Sendefrequenz betrage $f_{\rm S} = 2 \ {\rm GHz}$.
Die Grafik zeigt mögliche Bewegungsrichtungen des Empfängers.
* Die Richtung $\rm (A)$ wurde im $\text{Beispiel 4}$ betrachtet. Mit den aktuellen Parameterwerten ergibt sich
:'"`UNIQ-MathJax23-QINU`"'
* Für die Richtung $\rm (B)$ erhält man gemäß $\text{Beispiel 5}$ den gleichen Zahlenwert mit negativem Vorzeichen:
:'"`UNIQ-MathJax24-QINU`"'
* Die Fahrtrichtung $\rm (C)$ verläuft senkrecht $(\alpha = 90^\circ)$ zur Verbindungslinie Sender–Empfänger. In diesem Fall tritt keine Dopplerverschiebung auf:
:'"`UNIQ-MathJax25-QINU`"'
* Die Bewegungsrichtung $\rm (D)$ ist durch $\alpha = \ -135^\circ$ charakterisiert. Daraus resultiert:
:'"`UNIQ-MathJax26-QINU`"'
<div style="clear:both;">
</div>
</div>
==='"`UNIQ--h-4--QINU`"' Dopplerfrequenz und deren Verteilung===
Wir fassen die Aussagen der letzten Seite nochmals kurz zusammen, wobei wir von der zweiten, also der nicht–relativistischen Gleichung ausgehen:
*Bei einer Relativbewegung zwischen Sender (Quelle) und Empfänger (Beobachter) kommt es zu einer Verschiebung um die Dopplerfrequenz $f_{\rm D} = f_{\rm E} - f_{\rm S}$.
*Eine positive Dopplerfrequenz $(f_{\rm E} > f_{\rm S})$ ergibt sich dann, wenn sich Sender und Empfänger (relativ) aufeinander zu bewegen. Eine negative Dopplerfrequenz $(f_{\rm E} < f_{\rm S})$ bedeutet, dass sich Sender und Empfänger (direkt oder unter einem Winkel) voneinander entfernen.<br>
*Die maximale Frequenzverschiebung tritt auf, wenn sich Sender und Empfänger direkt aufeinander zu bewegen ⇒ Winkel $\alpha = 0^\circ$. Dieser Maximalwert hängt in erster Näherung von der Sendefrequenz $ f_{\rm S}$ und der Geschwindigkeit $v$ ab $(c = 3 \cdot 10^8 \, {\rm m/s}$ gibt die Lichtgeschwindigkeit an$)$: $f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.$
*Erfolgt die Relativbewegung unter einem beliebigen Winkel $\alpha$ zur Verbindungslinie Sender–Empfänger, so entsteht eine Dopplerverschiebung um
:\[f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha)
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} - \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \le f_{\rm D} \le + \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max}
\hspace{0.05cm}.\]
<div class="bluebox">
$\text{Fazit:}$ Unter der Annahme gleichwahrscheinlicher Bewegungsrichtungen $($Gleichverteilung für den Winkel $\alpha$ im Bereich $- \pi \le \alpha \le +\pi)$ ergibt sich für die Wahrscheinlichkeitsdichtefunktion $($hier mit „wdf” bezeichnet$)$ der Dopplerfrequenz im Bereich $- f_\text{D, max} \le f_{\rm D} \le + f_\text{D, max}$:
:\[{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } }
\hspace{0.05cm}.\]
Außerhalb des Bereichs zwischen $-f_{\rm D}$ und $+f_{\rm D}$ hat die Wahrscheinlichkeitsdichtefunktion stets den Wert Null.
[[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh-Prozesses#Dopplerfrequenz_und_deren_Verteilung|$\text{Herleitung}$]] über die „Nichtlineare Transformation von Zufallsgrößen”
<div style="clear:both;">
</div>
</div><br>
==='"`UNIQ--h-5--QINU`"' Leistungsdichtespektrum bei Rayleigh–Fading ===
Wir setzen nun eine in alle Richtungen gleich abstrahlende Antenne voraus. Dann ist das Doppler–$\rm LDS$ (Leistungsdichtespektrum) formgleich mit der $\rm WDF$ (Wahrscheinlichkeitsdichtefunktion) der Dopplerfrequenzen.
*Für die Inphasekomponente ${\it \Phi}_x(f_{\rm D})$ des LDS muss die WDF noch mit der Leistung $\sigma^2$ des Gaußprozesses multipliziert werden.
*Für das resultierende LDS ${\it \Phi}_z(f_{\rm D})$ des komplexen Faktors $z(t) = x(t) + {\rm j} \cdot y(t) $ gilt nach Verdoppelung:
:\[{\it \Phi}_z(f_{\rm D}) =
\left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\
0 \end{array} \right.\quad
\begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} |f_{\rm D}| \le f_{\rm D, \hspace{0.05cm} max}
\\ {\rm sonst} \\ \end{array}
\hspace{0.05cm}.\]
Man nennt diesen Verlauf nach [http://ethw.org/William_C._Jakes,_Jr. William C. Jakes Jr.] das '''Jakes–Spektrum'''. Die Verdoppelung ist notwendig, da bisher nur der Beitrag des Realteils $x(t)$ betrachtet wurde. <br>
[[File:P_ID2117__Mob_T_1_3_S4_v2.png|right|frame|Doppler–LDS und Zeitfunktion (Betrag in dB) bei Rayleigh-Fading mit Dopplereffekt]]
<div class="greybox">
$\text{Beispiel 7:}$ Links dargestellt ist das Jakes–Spektrum
*für $f_{\rm D, \hspace{0.05cm} max} = 50 \ \rm Hz$ (blaue Kurve) bzw.
*für $f_{\rm D, \hspace{0.05cm} max} = 100 \ \rm Hz$ (rote Kurve).
Beim [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_GSM#Zellularstruktur_von_GSM|GSM–D–Netz]] $(f_{\rm S} = 900 \ \rm MHz)$ entsprechen diese Werte den Geschwindigkeiten $v = 60 \ \rm km/h$ bzw. $v = 120 \ \rm km/h$.
Beim E–Netz $(f_{\rm S} = 1.8 \ \rm GHz)$ gelten diese Werte für halb so große Geschwindigkeiten: $v = 30 \ \rm km/h$ bzw. $v = 60 \ \rm km/h$.
Das rechte Bild zeigt den logarithmierten Betrag von $z(t)$:
*Man erkennt das doppelt so schnelle Fading des roten Kurvenverlaufs.
*Die Rayleigh–WDF (Amplitudenverteilung) ist unabhängig von $f_{\rm D, \hspace{0.05cm} max}$ und deshalb für beide Fälle gleich.
<div style="clear:both;">
</div>
</div><br>
=='"`UNIQ--h-6--QINU`"'Exercises==
[[File:Exercises_binomial_fertig.png|right]]
*Wählen Sie zunächst die Nummer '''1''' ... '''9''' der zu bearbeitenden Aufgabe.
*Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
*Lösung nach Drücken von „Musterlösung”.
*Die Nummer '''0''' entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
*In den folgenden Beschreibungen sind $f_{\rm S}$, $f_{\rm E}$ und $f_{\rm D}$ jeweils auf die Bezugsfrequenz $f_{\rm 0}$ normiert.
<br clear="all">
<div class="bluebox">
'''(1)''' Zunächst betrachten wir die relativistische Einstellung „Exakt”. Der Sender bewegt sich mit $v/c = 0.8$, die Sendefrequenz sei $f_{\rm S}= 1$.<br> Welche Empfangsfrequenzen $f_{\rm E}$ ergeben sich bei beiden Bewegungsrichtungen? Wie groß ist jeweils die Dopplerfrequenz $f_{\rm D}$?
<div style="clear:both;">
</div>
</div>
:* Nähert sich der Sender unter dem Winkel $\varphi=0^\circ$ dem Empfänger an, ergibt sich die Empfangsfrequenz $f_{\rm E}= 3$ ⇒ $f_{\rm D}= f_{\rm E} - f_{\rm S}= 2$.
:* Entfernt sich der Sender vom Empfänger $($für $\varphi=0^\circ$, wenn er diesen überholt, oder $\varphi=180^\circ)$, dann: $f_{\rm E}= 0.333$ ⇒ $f_{\rm D}= -0.667$.
:* Gleiches Ergebnis bei ruhendem Sender und sich bewegendem Empfänger: Kommen sich beide näher, dann gilt $f_{\rm D}= 2$, sonst $f_{\rm D}= -0.667$.
<div class="bluebox">
'''(2)''' Die Einstellungen bleiben weitgehend erhalten. Wie ändern sich sich die Ergebnisse gegenüber '''(1)''' mit der Sendefrequenz $f_{\rm S}= 1.5$?<br> Tipp für eine möglichst zeitsparende Versuchsdurchführung: Schalten Sie abwechselnd zwischen „Rechts” und „Links” hin und her.
<div style="clear:both;">
</div>
</div>
:* Bewegungsrichtung $\varphi=0^\circ$: $f_{\rm E}= 4.5$ ⇒ $f_{\rm D}= f_{\rm E} - f_{\rm S}= 3$. Somit: $f_{\rm E}/f_{\rm S}= 3$, $f_{\rm D}/f_{\rm S}= 2$ ⇒ Beides wie in '''(1)'''.
:* Bewegungsrichtung $\varphi=180^\circ$: $f_{\rm E}= 0.5$ ⇒ $f_{\rm D}= -1$. Somit: $f_{\rm E}/f_{\rm S}= 0.333$, $f_{\rm D}/f_{\rm S}= -0.667$ ⇒ Beides wie in '''(1)'''.
<div class="bluebox">
'''(3)''' Weiterhin relativistische Einstellung „Exakt”. Der Sender bewegt sich nun mit Geschwindigkeit $v/c = 0.4$ und die Sendefrequenz sei $f_{\rm S}= 2$.<br> Welche Frequenzen $f_{\rm D}$ und $f_{\rm E}$ ergeben sich bei beiden Bewegungsrichtungen? Wählen Sie wieder abwechselnd „Rechts” bzw. „Links”.
<div style="clear:both;">
</div>
</div>
:* Bewegungsrichtung $\varphi=0^\circ$: Empfangsfrequenz $f_{\rm E}= 3.055$ ⇒ Dopplerfrequenz $f_{\rm D}= 1.055$. ⇒ $f_{\rm E}/f_{\rm S}= 1.528$, $f_{\rm D}/f_{\rm S}= 0.528$.
:* Bewegungsrichtung $\varphi=180^\circ$: Empfangsfrequenz $f_{\rm E}= 1.309$ ⇒ Dopplerfrequenz $f_{\rm D}= -0.691$. ⇒ $f_{\rm E}/f_{\rm S}= 0.655$, $f_{\rm D}/f_{\rm S}= -0.346$.
<div class="bluebox">
'''(4)''' Es gelten weiter die bisherigen Voraussetzungen, aber nun die Einstellung „Näherung”. Welche Unterschiede ergeben sich gegenüber '''(3)'''?
<div style="clear:both;">
</div>
</div>
:* Bewegungsrichtung $\varphi=0^\circ$: Empfangsfrequenz $f_{\rm E}= 2.8$ ⇒ Dopplerfrequenz $f_{\rm D}= f_{\rm E} - f_{\rm S}= 0.8$ ⇒ $f_{\rm E}/f_{\rm S}= 1.4$, $f_{\rm D}/f_{\rm S}= 0.4$.
:* Bewegungsrichtung $\varphi=180^\circ$: Empfangsfrequenz $f_{\rm E}= 1.2$ ⇒ Dopplerfrequenz $f_{\rm D}= -0.8$. ⇒ $f_{\rm E}/f_{\rm S}= 0.6$, $f_{\rm D}/f_{\rm S}= -0.4$.
:* Mit „Näherung”: Für beide $f_{\rm D}$ gleiche Zahlenwerte mit verschiedenen Vorzeichen. Bei „Exakt” ist diese Symmetrie nicht gegeben.
<div class="bluebox">
'''(5)''' Es gelte weiterhin $f_{\rm S}= 2$. Bis zu welcher Geschwingkeit $(v/c)$ ist der relative Fehler zwischen „Näherung” und „Exakt” betragsmäßig $<5\%$?
<div style="clear:both;">
</div>
</div>
:* Mit $v/c =0.08$ und „Exakt” erhält man für die Dopplerfrequenzen $f_{\rm D}= 0.167$ bzw. $f_{\rm D}= -0.154$ und mit „Näherung” $f_{\rm D}= \pm0.16$.
:* Somit ist die relative Abweichung „(Näherung – Exakt)/Exakt” gleich $0.16/0.167-1=-4.2\%$ bzw. $(-0.16)/(-0.154)-1=+3.9\%$.
:* Mit $v/c =0.1$ sind die Abweichungen betragsmäßig $>5\%$. Für $v < c/10 = 30\hspace{0.05cm}000$ km/s ist die Dopplerfrequenz–Näherung ausreichend.
<div class="bluebox">
'''(6)''' Hier und in den nachfolgenden Aufgaben soll gelten: $f_{\rm S}= 1$, $v/c= 0.4$ ⇒ $f_{\rm D} = f_{\rm S} \cdot v/c \cdot \cos(\alpha)$. Mit $\cos(\alpha) = \pm 1$: $f_{\rm D}/f_{\rm S} =\pm 0.4$.<br> Welche normierten Dopplerfrequenzen ergeben sich mit dem eingestellten Startkoordinaten $(300,\ 50)$ und der Bewegungsrichtung $\varphi=-45^\circ$?
<div style="clear:both;">
</div>
</div>
:* Hier bewegt sich der Sender direkt auf den Empfänger zu $(\alpha=0^\circ)$ oder entfernt sich von ihm $(\alpha=180^\circ)$.
:* Gleiche Konstellation wie mit dem Startpunkt $(300,\ 200)$ und $\varphi=0^\circ$. Deshalb gilt auch hier für die Dopplerfrequenz: $f_{\rm D}/f_{\rm S} =\pm 0.4$.
:* Nachdem der Sender an einer Begrenzung „reflektiert” wurde, sind beliebige Winkel $\alpha$ und entsprechend mehr Dopplerfrequenzen möglich.
<div class="bluebox">
'''(7)''' Der Sender liegt fest bei $(S_x = 0,\ S_y =10),$ der Empfänger bewegt sich horizontal nach links bzw. rechts $(v/c = 0.4, \hspace{0.3cm}\varphi=0^\circ)$.<br> Beobachten und interpretieren Sie die zeitliche Änderung der Dopplerfrequenz $f_{\rm D}$.
<div style="clear:both;">
</div>
</div>
:* Wie in '''(6)''' sind auch hier nur Werte zwischen $f_{\rm D}=0.4$ und $f_{\rm D}=-0.4$ möglich, aber nun alle Zwischenwerte $(-0.4 \le f_{\rm D} \le +0.4)$.
:* Mit „Step” erkennen Sie: $f_{\rm D}\equiv0$ tritt nur auf, wenn der Empfänger genau unter dem Sender liegt $(\alpha=\pm 90^\circ$, je nach Fahrtrichtung$)$.
:* Dopplerfrequenzen an den Rändern sind sehr viel häufiger: $|f_{\rm D}| = 0.4 -\varepsilon$, wobei $\varepsilon$ eine kleine positive Größe angibt.
:* Schon aus diesem Versuch wird der prinzipielle Verlauf von Doppler–WDF und Doppler–LDS ⇒ „Jakes–Spektrum” erklärbar.
<div class="bluebox">
'''(8)''' Was ändert sich, wenn der Sender bei sonst gleichen Einstellungen fest am oberen Rand der Grafikfläche in der Mitte liegt $(0,\ 200) $?
<div style="clear:both;">
</div>
</div>
:* Die Dopplerwerte $f_{\rm D} \approx0$ werden häufiger, solche an den Rändern seltener. keine Werte $|f_{\rm D}| > 0.325$ aufgrund der begrenzten Zeichenfläche.
<div class="bluebox">
'''(9)''' Der Sender liegt bei $S_x = 300,\ S_y =200)$, der Empfänger bewegt sich mit $v/c = 0.4$ unter dem Winkel $\varphi=60^\circ$.<br> Überlegen Sie sich den Zusammenhang zwischen $\varphi$ und $\alpha$.
<div style="clear:both;">
</div>
</div>
:* Musterlösungen fehlen noch
=='"`UNIQ--h-7--QINU`"'Applet Manual==
[[File:Handhabung_binomial.png|left|600px]]
'''(A)''' Vorauswahl für blauen Parametersatz
'''(B)''' Parametereingabe $I$ und $p$ per Slider
'''(C)''' Vorauswahl für roten Parametersatz
'''(D)''' Parametereingabe $\lambda$ per Slider
'''(E)''' Graphische Darstellung der Verteilungen
'''(F)''' Momentenausgabe für blauen Parametersatz
'''(G)''' Momentenausgabe für roten Parametersatz
'''(H)''' Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
'''( I )''' Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
About the Authors
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2009 von Alexander Happach im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Andre Schulz (Bachelorarbeit LB, Betreuer: Benedikt Leible und Tasnád Kernetzky ) unter „HTML5” neu gestaltet.