Exercise 4.7Z: Signal Shapes for ASK, BPSK and DPSK
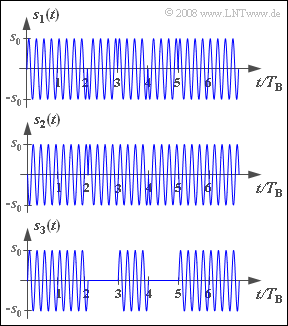
Die Abbildung zeigt jeweils ausgehend vom gleichen Quellensignal $q(t)$ die Sendesignale bei
- Amplitude Shift Keying (ASK),
- Binary Phase Shift Keying (BPSK),
- Differential Phase Shift Keying (DPSK).
Die Sendesignale sind hier allgemein mit $s_1(t)$, $s_2(t)$ und $s_3(t)$ bezeichnet. Die Zuordnung zu den vorgegebenen Modulationsverfahren soll von Ihnen vorgenommen werden.
Außerdem soll für alle Signale die jeweilige mittlere Energie pro Bit ⇒ $E_{\rm B}$ in „Ws” angegeben werden, wobei folgende Annahmen getroffen werden können:
- Die (maximale) Hüllkurve aller trägerfrequenzmodulierten Signale ist $s_0 = 2\ \rm V$.
- Die Bitrate des redundanzfreien Quellensignals beträgt $R_{\rm B} = 1 \ \rm Mbit/s$.
- Die Modulatoren arbeiten mit einem Arbeitswiderstand von $R = 50 \ \rm Ω$.
Beispielsweise würde bei (bipolarer) Basisbandübertragung mit der Symboldauer $T_{\rm } = 1/R_{\rm }$ gelten:
- $$ E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{50 \,{\rm V/A}}= 8 \cdot 10^{-8} \,{\rm Ws}= 0.08 \,\,{\rm µ Ws}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Lineare digitale Modulation.
- Bezug genommen wird aber auch auf das Kapitel Grundlagen der codierten Übertragung im Buch „Digitalsignalübertragung”.
- Die Leistungen sind in $\rm V^2$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$.
Fragebogen
Musterlösung
- Das ASK–Signal ergibt sich aus der Multiplikation des hier sinusförmigen Trägersignals $z(t)$ mit dem unipolaren Quellensignal $q(t)$.
- Es ist offensichtlich, dass $s_3(t)$ ein solches ASK–Signal beschreibt.
- Die unipolaren Amplitudenkoeffizienten des Quellensignals lauten $1,\ 1,\ 0,\ 1,\ 0,\ 1,\ 1$.
(2) Gegenüber der bipolaren Basisbandübertragung sind bei der ASK folgende Änderungen zu erkennen:
- Die Energie wird wegen der Multiplikation mit dem Sinussignal halbiert.
- Da $q(t)$ als redundanzfrei vorausgesetzt wird, gilt in der Hälfte der Zeit $s_3(t) = 0$, wodurch die Energie nochmals halbiert wird.
Damit ergibt sich:
- $$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{4 \cdot R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4 \cdot 50 \,{\rm V/A}}= 2 \cdot 10^{-8} \,{\rm Ws}\hspace{0.15cm}\underline {= 0.02 \,\,{\rm µ Ws}}.$$
(3) Richtig ist der Lösungsvorschlag 1:
- Typisch für die BPSK sind Phasensprünge.
- Da stets das gleiche Quellensignal vorausgesetzt wurde, treten diese Phasensprünge genau dann auf, wenn es im ASK–Signal $s_3(t)$ einen Symbolwechsel gibt.
(4) Von der unter (2) genannten Veränderung gegenüber der Basisbandübertragung ist bei BPSK nur die erste zutreffend. Damit gilt:
- $$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{2 \cdot R} \hspace{0.15cm}\underline {= 0.04 \,\,{\rm µ Ws}}.$$
(5) Wie bereits zu vermuten ist, lautet die richtige Antwort $s_2(t)$ ⇒ Lösungsvorschlag 2:
- Der DPSK–Modulator arbeitet wie folgt, wobei $m_0 = -1$ vorausgesetzt wird:
- $$ m_0 = -1, \hspace{0.1cm}a_1 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_1 = -1,$$
- $$m_1 = -1, \hspace{0.1cm}a_2 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_2 = -1,$$
- $$m_2 = -1, \hspace{0.1cm}a_3 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_3 = +1,$$
- $$m_3 = +1, \hspace{0.1cm}a_4 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_4 = +1,$$
- $$m_4 = +1, \hspace{0.1cm}a_5 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_5 = -1,$$
- $$m_5 = -1, \hspace{0.1cm}a_6 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_6 = -1, \,\,{\rm usw.}$$
(6) Ein Vergleich der beiden Signale $s_1(t)$ und $s_2(t)$ zeigt, dass sich hinsichtlich der Signalenergie nichts ändert.
- Daraus folgt: Die DPSK weist die genau gleiche Signalenergie auf wie die BPSK:
- $$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{2 \cdot R} \hspace{0.15cm}\underline {= 0.04 \,\,{\rm µ Ws}}.$$