Exercise 1.1: Dual Slope Loss Model

• Return to book

Dual-slope path loss diagram

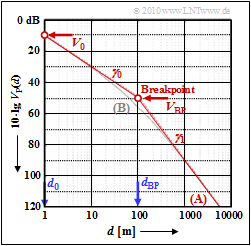
To simulate path loss in an urban environment, the asymptotic dual-slope model is often used, which is shown as a red curve in the diagram.  This simple model is characterized by two linear sections separated by the so-called breakpoint  $\rm (BP)$. The variable name "$V$" stands for "Verlust", which is the German word for "loss":

• For  $d \le d_{\rm BP}$  and the exponent   $\gamma_0$  we have:

$$V_{\rm S}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_0})\hspace{0.05cm}.$$

• For  $d > d_{\rm BP}$  we must apply the path loss exponent  $\gamma_1$  where  $\gamma_1 > \gamma_0$:

$$V_{\rm S}(d) = V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_{\rm BP}})\hspace{0.05cm}.$$

In these equations, the variables are:

• $V_0$  is the path loss (in dB) at  $d_0$  (normalization distance).
• $V_{\rm BP}$  is the path loss (in dB) at  $d=d_{\rm BP}$  ("Breakpoint").

The graph applies to the model parameters

$$d_0 = 1\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}d_{\rm BP} = 100\,{\rm m}\hspace{0.05cm},\hspace{0.2cm} V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$$

In the questions, this piece-wise defined profile is called  $\rm A$.

The second curve is the profile  $\rm B$  given by the following equation:

$$V_{\rm S}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )\hspace{0.05cm}.$$

With this dual model, the entire distance course can be written in closed form, and the received power depends on the distance  $d$  according to the following equation:

$$P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm tot}}{V_{\rm S}(d)} \hspace{0.05cm},\hspace{0.2cm}V_{\rm S}(d) = 10^{V_{\rm S}(d)/10} \hspace{0.05cm}.$$

Here, all parameters are in natural units (not in dB).  The transmit power is assumed to be  $P_{\rm S} = 5 \ \rm W$ .  The other quantities have the following meanings and values:

• $10 \cdot \lg \ G_{\rm S} = 17 \ \rm dB$  (gain of the transmit antenna),
• $10 \cdot \lg \ G_{\rm E} = -3 \ \ \rm dB$  (gain of receiving antenna – so actually a loss),
• $10 \cdot \lg \ V_{\rm tot} = 4 \ \ \rm dB$  (loss through feeds).

Notes:

• This task belongs to the chapter  Distance dependent attenuation and shading.
• If the profile  $\rm B$  were

$$V_{\rm S}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right )$$

then profile  $\rm A$  and profile  $\rm B$  would be identical for  $d ≥ d_{\rm BP}$.

• In this case, however, profile  $\rm B$  would be above profile  $\rm A$  for   $d < d_{\rm BP}$, suggesting clearly too good conditions.
• For example,   $d = d_0 = 1 \ \ \rm m$  with the given numerical values gives a result that is   $40 \ \ \rm dB$  too good:

$$V_{\rm S}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right ) =10\,{\rm dB} + 2 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({1}/{100} \right ) = -30\,{\rm dB} \hspace{0.05cm}.$$

Questions

1

How large is the path loss $($in  $\rm dB)$  after  $d= 100 \ \rm m$  according to profile  $\rm A$?

$V_{\rm S}(d = 100 \ \rm m) \ = \ $ $\ \rm dB$

2

How large is the path loss $($in  $\rm dB)$  after  $d= 100 \ \rm m$  according to profile  $\rm B$?

$V_{\rm S}(d = 100 \ \rm m) \ = \ $ $\ \rm dB$

3

What is the received power after  $100 \ \ \rm m$  with both profiles?

Profile $\text{A:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ $\ \ \rm mW$

Profile $\text{B:} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ $\ \ \rm mW$

4

How big is the deviation  $ΔV_{\rm S}$  between profile  $\rm A$  and  $\rm B$  at  $d = 50 \ \rm m$?

$ΔV_{\rm P}(d = 50 \ \rm m) \ = \ $ $\ \rm dB$

5

How big is the deviation  $ΔV_{\rm S}$  between profile  $\rm A$  and  $\rm B$  at  $d = 200 \ \rm m$?

$ΔV_{\rm P}(d = 200 \ \rm m)\ = \ $ $\ \rm dB$

Solutions

Solution

(1)  You can see directly from the graphic that the profile  $\rm (A)$  with the two linear sections at the breakpoint  $(d = 100 \ \rm m)$  gives the following result:

$$V_{\rm S}(d = 100\,{\rm m})\hspace{0.15cm} \underline{= 50\,{\rm dB}} \hspace{0.05cm}.$$

(2)  With the profile  $\rm (B)$  on the other hand, using  $V_0 = 10 \ \rm dB$,  $\gamma_0 = 2$  and  $\gamma_1 = 4$:

$$V_{\rm S}(d = 100\,{\rm m}) = 10\,{\rm dB} + 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(100)+ 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(2) \hspace{0.15cm} \underline{\approx 56\,{\rm dB}} \hspace{0.05cm}.$$

(3)  The antenna gains from the transmitter  $(+17 \ \rm dB)$  and receiver  $(-3 \ \rm dB)$  and the internal losses of the base station  $(+4 \ \rm dB)$  can be combined to

$$10 \cdot {\rm lg}\hspace{0.1cm} G = 10 \cdot {\rm lg}\hspace{0.1cm} G_{\rm S} + 10 \cdot {\rm lg} \hspace{0.1cm} G_{\rm E} - 10 \cdot {\rm lg}\hspace{0.1cm} V_{\rm tot} = 17\,{\rm dB} -3\,{\rm dB} - 4\,{\rm dB} = 10\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {G = 10} \hspace{0.05cm}.$$

• For the profile  $\rm (A)$  the following path loss occurred:

$$V_{\rm S}(d = 100\,{\rm m})\hspace{0.05cm} {= 50\,{\rm dB}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_{\rm P} = 10^5 \hspace{0.05cm}.$$

This gives you for the received power after  $d = 100\ \rm m$:

$$P_{\rm E}(d = 100\,{\rm m}) = \frac{P_{\rm S} \cdot G}{K_{\rm P}} = \frac{5\,{\,} \cdot 10}{10^5}\hspace{0.15cm} \underline{= 0.5\,{\rm mW}} \hspace{0.05cm}.$$

• For profile  $\rm (B)$  the received power is about  $4$  times smaller:

$$P_{\rm E}(d = 100\,{\rm m}) = \frac{5\,{\rm W} \cdot 10}{10^{5.6}}\approx \frac{5\,{\rm W} \cdot 10}{4 \cdot 10^{5}}\hspace{0.15cm} \underline{= 0.125\,{\rm mW}} \hspace{0.05cm}.$$

(4)  Below the breakpoint  $(d < 100 \ \rm m)$, the deviation is determined by the last summand of profile  $\rm (B)$:

$${\rm \Delta}V_{\rm S}(d = 50\,{\rm m}) = (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )= (4-2) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (1.5)\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$

(5)  Here the profile  $\rm (A)$  with  $V_{\rm BP} = 50 \ \rm dB$  gives:

$$V_{\rm S}(d = 200\,{\rm m}) = 50\,{\rm dB} + 4 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (2)\hspace{0.15cm} {\approx 62\,{\rm dB}} \hspace{0.05cm}.$$

• On the other hand, the profile  $\rm (B)$  leads to the result:

$$V_{\rm S}(d = 200\,{\rm m}) = 50\,{\rm dB} + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (200) + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (3) = 10\,{\rm dB} + 46\,{\rm dB} + 9.5\,{\rm dB} \hspace{0.15cm} {\approx 65.5\,{\rm dB}}$$

$$\Rightarrow \hspace{0.3cm} {\rm \Delta}V_{\rm P}(d = 200\,{\rm m}) = 65.5\,{\rm dB} - 62\,{\rm dB}\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$

• You can see that  $\Delta V_{\rm S}$  is almost symmetrical to  $d = d_{\rm BP}$  if you plot the distance  $d$  logarithmically as in the given graph.