Exercise 1.1Z: ISDN Connection

a telephone connection scenario

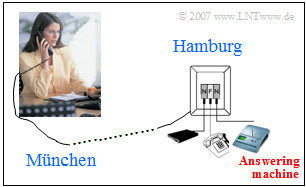
We consider the scenario shown in the picture:

A woman from Munich dials a number in Hamburg with her ISDN phone. However, she cannot reach the person she wants to talk to, so she leaves him a message on tape.

The distortion-free connection is fully described by

a damping factor $\alpha$,
a term $\tau$, and
the current signal-to-noise ratio (SNR)

Notes: The task shall establish a relation between this real scenario and the functional units of a general message transmission system mentioned in Theorieteil .

Questions

Solutions

Solution

(1) The first two statements are correct:

The speech signal ${q(t)}$ must first be converted into an electrical signal and then prepared for transmission.
For ISDN the transmit signal is ${s(t)}$ digital.

(2) Correct are the solutions 3 and 4:

The received signal ${r(t)}$ is always analog due to the unavoidable thermal noise.
The message sink is the answering machine
In an ideal transmission system $v(t) = {q(t)}$ should apply.
Due to the additive noise term ${n(t)}$, the damping $\alpha$ and the running time $\tau$ but applies here:

$$v(t) = \alpha \cdot q ( t - \tau) + n(t).$$

By our definitions, this is a distortion-free system.

	The received signal $r(t)$ is digital.
	The news sink is the telephone set in Hamburg.
	The news sink is the answering machine.
	The following applies $v(t) = \alpha \cdot q(t - \tau ) + {n(t)}$.
	There is an ideal transmission system.

	The news source is the caller. The source signal ${q(t)}$ is the acoustic wave of her voice signal.
	The unit designated "transmitter" contains, among other things, a signal converter and a modulator.
	The transmit signal $s(t)$ is analog.