Exercise 1.2Z: Puls Code Modulation

Components of pulse code modulation

All modern communication systems are digital. The principle of digital transmission of speech signals goes back to Alec Reeves , who invented the so-called Pulscodemodulation (PCM) already at 1938.

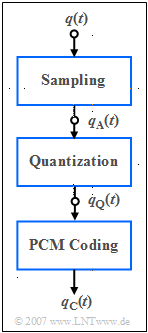
On the right you see the (simplified) block diagram of the PCM transmitter with three functional units:

The band-limited speech signal ${q(t)}$ is sampled, where the Abtasttheorem is observed, and yields the sampled signal $q_{\rm A}(t)$.
Each sample $q_{\rm A}(t)$ is mapped to one of $M = 2^N$ and results in the quantized signal $q_{\rm Q}(t)$.
Each individual quantized value is represented by a code sequence of $N$ binary symbols and results in the coded signal $q_{\rm C}(t)$.

In this task only the different signals of the PCM transmitter are to be classified. Later tasks will deal with other properties of pulse code modulation.

Notes: This task belongs to the chapter Klassifizierung von Signalen.

Questions

Solutions

Solution

(1) Correct are the solutions 1, 2 and 4:

The source signal ${q(t)}$ is analog, i.e. time- and value-continuous.
Im Allgemeinen macht es keinen Sinn, ein deterministisches Signal zu übertragen.
Für die mathematische Beschreibung eignet sich ein deterministisches Quellensignal – wie zum Beispiel ein periodisches Signal – besser als ein Zufallssignal.
Deterministische Signale werden auch für den Testbetrieb herangezogen, um erkannte Fehlfunktionen rekonstruieren zu können.

(2) Correct are the solution suggestions 2 and 3:

The signal $q_{\rm A}(t)$ after sampling is still value-continuous, but now time-discrete.
The sampling frequency $f_{\rm A}$ is given by the so-called sampling theorem .
The greater the maximum frequency $f_{\rm N,\,max}$ of the message signal, the greater must $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ can be selected.

(3) Correct are the solution suggestions 1 and 3:

The quantized signal $q_{\rm Q}(t)$ is time and value discrete, where the number of steps are $M = 2^8 = 256$
A binary signal, on the other hand, is a discrete value signal with the number of steps $M = 2$.

(4) Richtig sind hier die Lösungsvorschläge 1, 3 und 5:

The coded signal $q_{\rm C}(t)$ is binary $($level number $M = 2)$ with bit duration $T_{\rm B} = T_{\rm A}/8$.

	In normal operation ${q(t)}$ is a stochastic signal.
	A deterministic source signal is only useful in test operation or for theoretical investigations.
	${q(t)}$ is a time-discrete signal.
	${q(t)}$ is a continuous value signal.

	$q_{\rm Q}(t)$ is a time-discrete signal.
	$q_{\rm Q}(t)$ is a discrete-valued with signal $M = 8$ possible values.
	$q_{\rm Q}(t)$ is a discrete-valued with signal $M = 256$ possible values.
	$q_{\rm Q}(t)$ is a binary signal.

	$q_{\rm C}(t)$ is a time-discrete signal.
	$q_{\rm C}(t)$ is a discrete-valued signal with $M = 8$ possible values.
	$q_{\rm C}(t)$ is a binary signal.
	When sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}$.
	For sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}/8$.

	$q_{\rm A}(t)$ is a discrete-valued signal.
	$q_{\rm A}(t)$ is a time-discrete signal.
	The higher the maximum frequency of the message signal, the higher the sampling rate must be selected.