Exercise 2.4: Rectified Cosine
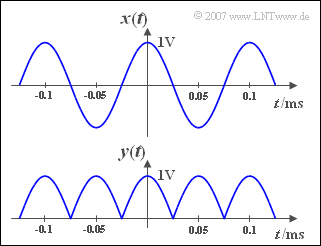
Ein Cosinussignal $x(t)$ mit der Amplitude $1\,\rm{V}$ und der Frequenz $f_0= 10\,\rm{kHz}$ wird an den Eingang eines Doppelweggleichrichters gelegt. An dessen Ausgang ergibt sich das Signal $y(t)$, das in der Grafik unten dargestellt ist.
Bei den Teilaufgaben (6) und (7) wird auch das Fehlersignal $\varepsilon_3(t) = y_3(t) - y(t)$ verwendet. Dieses beschreibt die Differenz zwischen der auf lediglich $N = 3$ Koeffizienten begrenzten Fourierreihe ⇒ $y_3(t)$ und dem tatsächlichen Ausgangssignal $y(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fourierreihe.
- Zur Lösung der Aufgabe können Sie das folgende bestimmte Integral benutzen $(n$ sei ganzzahlig$)$:
- $$\int ^{\pi /2}_{-\pi /2}\cos(u)\cdot\cos(2nu)\,{\rm d}u = (-1)^{n+1}\cdot\frac{2}{4n^2-1}.$$
- Eine kompakte Zusammenfassung der Thematik finden Sie im Lernvideo Zur Berechnung der Fourierkoeffizienten.
Fragebogen
Musterlösung
- Aus der Signalfrequenz $f_0= 10\,\rm{kHz}$ folgt $T_0 = 1/f_0 = 100\,µ\text{s}$.
- Das Cosinussignal ist gleichsignalfrei $(A_0 = 0)$ und wird durch einen einzigen Cosinuskoeffizienten – nämlich $A_1$ – vollständig beschrieben.
- Alle Sinuskoeffizienten sind $B_n \equiv 0$, da $x(t)$ eine gerade Funktion ist.
- Die Fourierreihendarstellung $x_3(t)$ bildet $x(t)$ fehlerfrei nach.
(2) Aufgrund der Doppelweggleichrichtung ergibt sich für die Periodendauer nunmehr der halbe Wert: $T_0 \hspace{0.1cm}\underline{= 50\,µ\text{s}}$.
- Bei allen nachfolgenden Punkten bezieht sich die Angabe $T_0$ auf diesen Wert, also auf die Periodendauer des Signals $y(t)$.
(3) Im Bereich von $–T_0/2$ bis $+T_0/2 \ (–25\,µ\text{s} \ \text{...} +25\,µ\text{s})$ ist $y(t) = x(t)$. Mit $f_x= 10\,\rm{kHz} = 1/(2T_0)$ gilt deshalb für diesen Abschnitt:
- $$y(t)={\rm 1V}\cdot\cos(2{\pi} f_0\hspace{0.05cm}t)={\rm 1V}\cdot\cos(\pi \cdot {t}/{T_0}).$$
- Daraus ergibt sich für den Gleichsignalanteil:
- $$A_0=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}y(t)\,{\rm d} t=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}{\rm 1V}\cdot\cos(\pi\cdot {t}/{T_0})\,{\rm d}t.$$
- Mit der Substitution $u = \pi \cdot t/T_0$ erhält man schließlich:
- $$A_0=\left. \frac{ {\rm 1V}}{\pi}\int_{-\pi /2}^{\pi/2}\cos(u)\,{\rm d}u=\frac{ {\rm 1V}}{\pi}\sin(u)\; \right| _{-\pi/2}^{\pi/2}=\frac{ {\rm 1V}\cdot 2}{\pi} \hspace{0.15cm}\underline{\approx 0.637\;{\rm V}}.$$
(4) Da $y(–t) = y(t)$ gilt, sind alle Sinuskoeffizienten $B_n = 0$. Damit ist auch $B_2 \hspace{0.1cm}\underline{= 0}$.
(5) Für die Koeffizienten $A_n$ gilt mit der Substitution $u = \pi \cdot t/T_0$ entsprechend dem angegebenen Integral:
- $$A_n = \frac{2{\rm V}}{T_0}\int_{-T_0/2}^{T_0/2}\cos(\pi\frac{t}{T_0})\cdot \cos(n\cdot 2\pi\frac{t}{T_0})\,{\rm d}t = \frac{2{\rm V}}{\pi}\int_{-\pi/2}^{\pi/2}\cos(u)\cdot \cos(2n u)\,{\rm d}u \quad \Rightarrow \quad A_n = \left( { - 1} \right)^{n + 1} \frac{{4\;{\rm{V}}}}{{{\rm{\pi }}\left( {4n^2 - 1} \right)}}.$$
Der Koeffizient $A_2$ ist damit gleich $-4 \,\text{V}/(15\pi) \hspace{0.1cm}\underline{\approx -\hspace{0.05cm}0.085 \, \text{V}}$.
(6) Für die endliche Fourierreihe mit $N = 3$ gilt allgemein:
- $$y_3(t)=\frac{2{\rm V}}{\pi} \cdot \left [ 1+{2}/{3} \cdot \cos(\omega_0t)-{2}/{15}\cdot \cos(2\omega_0t)+{2}/{35}\cdot \cos(3\omega_0t) \right ].$$
Zum Zeitpunkt $t = 0$ ist $y_3(0) \approx 1.0125 \ \rm V$; damit ergibt sich der Fehler zu $\varepsilon_3(t = 0) \hspace{0.15cm}\underline{= 0.0125 \,\text{V}}$ .
(7) Die Zeit $t = 25\,µ\text{s}$ entspricht der halben Periodendauer des Signals $y(t)$. Hierfür gilt wegen $\omega_0 \cdot T_0 = 2\pi$:
- $$y_3(T_0/2) = \frac{2{\rm V}}{\pi} \left [1+\frac{2}{3} \cdot \cos({\pi}) -\frac{2}{15}\cdot \cos(2\pi)+\frac{2}{35}\cdot \cos(3\pi)\right ]= \frac{2{\rm V}}{\pi}\left [1-\frac{2}{3}-\frac{2}{15}-\frac{2}{35}\right ] = \frac{2{\rm V}}{7\pi}\approx 0.091{\rm V}.$$
- Da $y(T_0/2) = 0$ ist, ergibt sich auch $\varepsilon_3(T_0/2) \hspace{0.15cm}\underline{\approx 0.091\,{\rm V}}$.
- Dieser Fehler ist um mehr als den Faktor $7$ größer als der Fehler bei $t = 0$, da $y(t)$ bei $t = T_0/2$ mehr hochfrequente Anteile besitzt (spitzförmiger Verlauf).
- Wird gefordert, dass der Fehler $\varepsilon_3(T_0/2)$ kleiner als $0.01$ sein soll, dann müssten mindestens $32$ Fourierkoeffizienten berücksichtigt werden.