Signal classification

Deterministic and Stochastic Signals

In every communication system both deterministic and stochastic signals occur.

$\text{Definition:}$ A deterministic signal exists, if its time functions $x(t)$ can be described completely in analytical form.

Since the time function $x(t)$ for all times $t$ is known and can be specified unambiguously, a spectral function $X(f)$ which can be calculated using the Fourier series or Fourier transform .

$\text{Definition:}$ One refers to a 'stochastic signal or to a random signal, if the signal course $x(t)$ is not - or at least not completely – describable in mathematical form. Such a signal cannot be predicted exactly for the future.

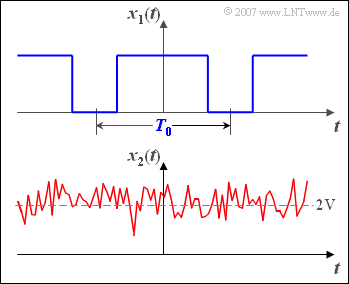
Example of a deterministic signal (top) and
a stochastic signal (bottom)

$\text{Example 1:}$ The graph shows time histories of a deterministic and a stochastic signal:

At the top a periodic square wave signal $x_1(t)$ with period duration $T_0$ ⇒ deterministic signal,
below a Gaussian noise signal $x_2(t)$ with the mean value $2\ \rm V$ ⇒ stochastic signal.

For such a non-deterministic signal $x_2(t)$ no spectral function $X_2(f)$ can be specified, since Fourier series/Fourier transform requires the exact knowledge of the time function for all times $t$

Information-carrying signals are always of stochastic nature. Their description as well as the definition of suitable parameters is given in the book Theory of Stochastic Signals.

However, the deterministic signals are also of great importance for communications engineering. Examples of this are:

test signals for the design of communication systems,
carrier signals for frequency multiplex systems, and
a pulse for sampling an analog signal or for time regeneration of a digital signal.

Causal and Non-Causal Signals

In communications engineering one often reckons with temporally unlimited signals; the definition range of the signal then extends from $t = -\infty$ to $t=+\infty$ .

In reality, however, there are no such signals, because every signal had to be switched on at some point. If one chooses - arbitrarily, but nevertheless meaningfully - the switch-on time $t = 0$ , then one comes to the following classification:

$\text{Definition:}$ A signal $x(t)$ is called causal, if it does not exist for all times $t < 0$ or is identical zero. If this condition is not fulfilled, a ‘’non-causal signal (or system) exists.

In this book „Signal representation” mostly causal signals and systems are considered. This has the following reasons:

Non-causal signals (and systems) are mathematically easier to handle than causal ones. For example, the spectral function can be determined here by means of Fourier transformations and one does not need extensive knowledge of function theory as in the Laplace transformation.
Non-causal signals and systems describe the situation completely and correctly, if one ignores the problem of the switch-on process and is therefore only interested in the steady state .

The description of causal signals and systems using the Laplace Transform is shown in the book Linear Time-Invariant Systems.

Causal and non-causal system

$\text{Example 2:}$ You can see a causal transmission system in the upper graphic:

If a unit step function $x(t)$ is applied to its input, then the output signal $y(t)$ can only increase from zero to its maximum value after time $t = 0$ .
Otherwise the causal connection that the effect cannot begin before the cause would not be fulfilled.

The causality In the lower pictureis no longer given. As you can easily see in this example, an additional runtime of one millisecond is enough to change from the non-causal to the causal representation.

Energy Limited and Power Limited Signals

At this place first two important signal description quantities must be introduced, namely the energy and the power.

In terms of physics, energy corresponds to work and has, for example, the unit "Ws".
The power is defined as "work per time" and therefore has the unit "W".

According to the elementary laws of electrical engineering, both values are dependent on the resistance $R$ . In order to eliminate this dependency, the resistance $R=1 \,\Omega$ is often used as a basis in communications engineering. Then the following definitions apply:

$\text{Definition:}$ The energy of the signal $x(t)$ is to calculate as follows:

$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$

$\text{Definition:}$ To calculate the (mean) power , $T_{\rm M}$ must be divided by the timebefore the limit crossing:

$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$

Where $T_{\rm M}$ is the assumed measurement duration during which the signal is observed, symmetrically with respect to the time origin $(t = 0)$ . In general, this time interval must be chosen very large; ideally $T_{\rm M}$ should be towards infinity.

If $x(t)$ denotes a stress curve with the unit $\text{V}$ , according to the above equations is for

the signal energy the unit $\text{V}^2\text{s}$ ,
the signal power the unit $\text{V}^2$ .

This statement also means: In the above definitions the reference resistance $R=1\,\Omega$ is already implicit.

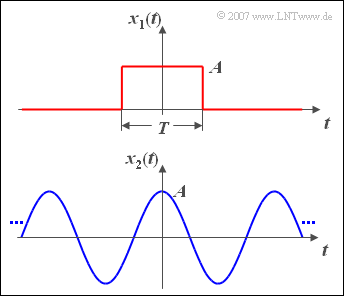
Energy limited and power limited signal

$\text{Example 3:}$ Now the energy and power of two exemplary signals are calculated.

The upper graphic shows a rectangular pulse $x_1(t)$ with amplitude $A$ and duration $T$ .

The signal energy of this pulse is $E_1 = A^2 \cdot T$ .
For the signal power, division by $T_{\rm M}$ and limit formation $(T_{\rm M} \to \infty)$ the value $P_1 = 0$ .

For the cosine signal $x_2(t)$ with amplitude $A$ applies according to the sketch below:

The signal power is equal to&nbsp regardless of the frequency; $P_2 = A^2/2$ .
The signal energy $E_2$ (integral over power for all times) is infinite.

With $A = 4 \ {\rm V}$ results for the power $P_2 = 8 \ {\rm V}^2$ . With the resistance of $R = 50 \,\,\Omega$ this corresponds to the physical power ${8}/{50} \,\,{\rm V}\hspace{-0.1cm}/{\Omega}= 160\,\, {\rm mW}$ .

According to this example there are the following classification characteristics:

$\text{Definition:}$ A signal $x(t)$ with finite energy $E_x$ and infinitely small power $(P_x = 0)$ is called energy limited.

Pulse-shaped signals like the signal $x_1(t)$ in the above example, energy is always limited. Mostly, the signal values here are different from zero only for a finite period of time. In other words: Such signals are often also time-limited.
But even signals that are unlimited in time can have a finite energy. In later chapters you will find more information about energy limited and therefore aperiodic signals, for example the Gaussian pulse and the Exponential pulse .

$\text{Definition:}$ A signal $x(t)$ with finite power $P_x$ and accordingly infinite energy $(E_x \to \infty)$ is called power limited.

All power limited signals are also infinitely extended in time.
Examples are the direct current signal and harmonic oscillations such as the cosine signal $x_2(t)$ in $\text{Example 3}$ , which are described in detail in chapter Periodic Signals.
Even most stochastic signals are power limited - see the book Theory of Stochastic Signals.

Value-Continuous and Value-Discrete Signals

$\text{Definition:}$ A signal is called value-continuous, if the decisive signal-parameter - for example the instantaneous value - can take all values of a continuum (for example of an interval) . In contrast, if only countable many different values are possible for the signal parameter, then the signal is value-discrete. The number of possible values is called the number of steps $M$ or the range of values.

Analog transmission systems always work with value-continuous signals.
For digital systems, on the other hand, most but not all signals are value-discrete.

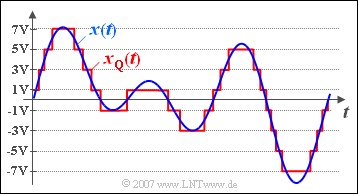
Value-continuous and value-discrete signal

$\text{Example 4:}$ The upper image shows in blue a section of a continuous-value signal $x(t)$ , which can take values between $\pm 8\ \rm V$ .

In red you can see the signal $x_{\rm Q}(t)$ discretised on $M = 8$ quantization steps with the possible signal values $\pm 1\ \rm V$ , $\pm 3\ \rm V$ , $\pm 5\ \rm V$ and $\pm 7\ \rm V$ .
For this signal $x_{\rm Q}(t)$ the instantaneous value was considered the decisive signal parameter.

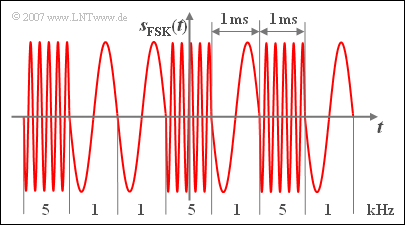
FSK-Signal - value-continuous and still binary

In an FSK system (Frequency Shift Keying) on the other hand, the instantaneous frequency is the essential signal parameter.

Therefore the signal $s_{\rm FSK}(t)$ shown below is also called discrete with the step number $M = 2$ and the possible frequencies $1 \ \ \rm kHz$ and $5 \ \ \rm kHz$ , although the instantaneous value is continuous in value.

Time Continuous and Time Discrete Signals

For the signals considered so far, the signal parameter was defined at any given time. Then it is called a time-continuous signal.

$\text{Definition:}$ With a time-discrete signal on the contrary, the signal parameter is defined only at the discrete points in time $t_\nu$ where these points in time are usually chosen equidistant: $t_\nu = \nu \cdot T_{\rm A}$ .

Since such a signal is created, for example, by sampling a time-continuous signal, we refer to $T_{\rm A}$ as the sampling time interval and its reciprocal $f_{\rm A} = 1/T_{\rm A}$ as the sampling frequency.

Furthermore applies:

A time-discrete signal $x(t)$ is completely determined by its series $\left \langle x_\nu \right \rangle$ of sampled values .
These sampled values can be either value-continuous or value-discrete.
The mathematical description of time-discrete signals is given in chapter Time Discrete Signal Representation .

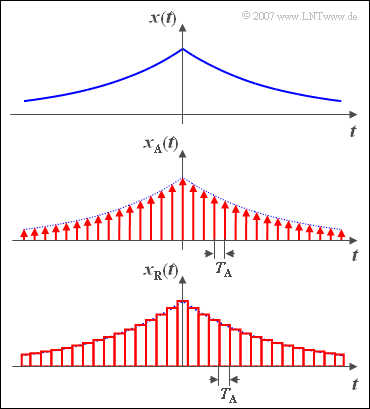
Time continuous and time discrete signal

$\text{Example 5:}$ The time discrete signal $x_{\rm A}(t)$ is obtained after sampling the time- and value continuous message signal $x(t)$ in distance $T_{\rm A}$ .

The time plot $x_{\rm R}(t)$ outlined below differs from the real time-discrete representation $x_{\rm A}(t)$ in that the infinitely narrow samples (mathematically describable with Dirac pulses) are replaced by rectangular pulses of duration $T_{\rm A}$ .

Such a signal can also be called time-discrete according to the above definition.

Analog and Digital Signals

Analog and digital signals

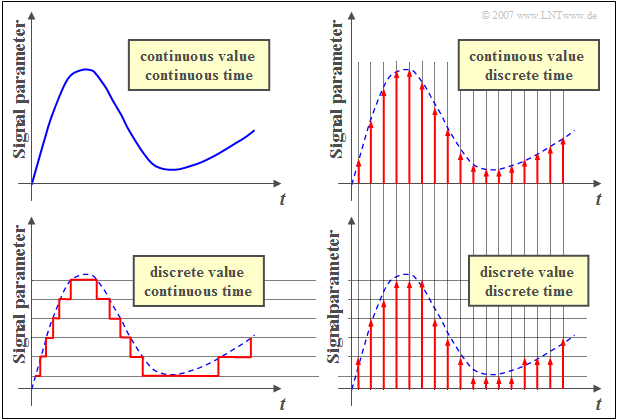
$\text{Example 6:}$ The following signal properties are illustrated in the diagram using an example:

„value-continuous" and "value-discrete", as well as
"time continuous" and "time discrete".

In addition, the following specifications apply:

$\text{Definition:}$ If a signal is both value– and time continuous, it is also called a analog signal. Such signals represent a continuous process continuously. Examples are speech–, music–, picture– and measurement signals.

$\text{Definition:}$ A digital signal , on the other hand, is always value– and time-discrete and the message contained therein consists of the symbols of a symbol set. For example, it can be a sampled and quantized (as well as coded in any form) voice–, music– or picture signal, but also a data signal when a file is downloaded from a server on the Internet.

Depending on the number of steps, digital signals are also known by other names, for example

with $M = 2$ : binary digital signal or Binary Signal,
with $M = 3$ : ternary digital signal or Ternary Signal,
with $M = 4$ : quaternary digital signal or Quaternary Signal.

The learning video Analog and Digital Signals summarizes the classification features discussed in this chapter in a compact way.

Exercises for the Chapter

Aufgabe 1.2: Signal Classification

Aufgabe 1.2Z: Pulscodemodulation