Some Basics of Algebra

1. Channel Coding
2. Reed–Solomon–Codes und deren Decodierung
3. Some Basics of Algebra

• Previous page
• Next page

• Previous page
• Next page

# ÜBERBLICK ZUM ZWEITEN HAUPTKAPITEL #

Dieses Kapitel behandelt die Reed–Solomon–Codes, die Anfang der 1960er Jahre von  Irving Stoy Reed  und  Gustave Solomon  erfunden wurden. Im Gegensatz zu den binären Blockcodes basieren diese auf einem Galoisfeld  ${\rm GF}(2^m)$  mit  $m > 1$. Sie arbeiten also mit mehrstufigen Symbolen anstelle von Binärzeichen (Bit).

Im Einzelnen werden in diesem Kapitel behandelt:

• Die Grundlagen der linearen Algebra:   Menge, Gruppe, Ring, Körper, endlicher Körper,
• die Definition von Erweiterungskörpern   ⇒   ${\rm GF}(2^m)$  und die zugehörigen Operationen,
• die Bedeutung von irreduziblen Polynomen und primitiven Elementen,
• die Beschreibungs– und Realisierungsmöglichkeiten eines Reed–Solomon–Codes,
• die Fehlerkorrektur eines solchen Codes beim Auslöschungskanal (BEC),
• die Decodierung mit Hilfe des Error Locator Polynoms   ⇒   Bounded Distance Decoding (BDD),
• die Blockfehlerwahrscheinlichkeit der Reed–Solomon–Codes und typische Anwendungen.

Definition eines Galoisfeldes

Bevor wir uns der Beschreibung der Reed–Solomon–Codes zuwenden können, benötigen wir einige algebraische Grundbegriffe. Wir beginnen mit den Eigenschaften des Galoisfeldes  ${\rm GF}(q)$, benannt nach dem Franzosen  Évariste Galois, dessen Biografie für einen Mathematiker eher ungewöhnlich ist.

$\text{Definition:}$  Ein  $\rm Galoisfeld$  ${\rm GF}(q)$  ist ein  endlicher Körper  mit  $q$  Elementen  $z_0$,  $z_1$,  ... ,  $z_{q-1}$, wenn die acht nachfolgend aufgeführten Aussagen  $\rm (A)$  ...  $\rm (H)$  hinsichtlich Addition („$+$”) und Multiplikation („$\cdot$”) zutreffen.

• Addition und Multiplikation sind hierbei modulo  $q$  zu verstehen.
• Die  $\rm Ordnung$  $q$  gibt die Anzahl der Elemente des Galoisfeldes an.

$\text{Kriterien eines Galoisfeldes:}$ 

$\rm (A)$  ${\rm GF}(q)$  ist in sich abgeschlossen $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Closure$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}(z_i + z_j)\in {\rm GF}(q),\hspace{0.15cm}(z_i \cdot z_j)\in {\rm GF}(q) \hspace{0.05cm}.$$

$\rm (B)$  Es gibt ein hinsichtlich der Addition neutrales Element $N_{\rm A}$, das so genannte Nullelement $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Identity \ for \ „\hspace{-0.05cm}+\hspace{0.05cm}”$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + z_j = z_i \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_j = N_{\rm A} = \text{ 0} \hspace{0.05cm}.$$

$\rm (C)$  Es gibt ein hinsichtlich der Multiplikation neutrales Element $N_{\rm M}$, das so genannte Einselement $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Identity \ for \ „\hspace{-0.05cm}·\hspace{0.05cm}”$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm}\Rightarrow \hspace{0.3cm} z_j = N_{\rm M} = {1} \hspace{0.05cm}.$$

$\rm (D)$  Für jedes  $z_i$  existiert eine additive Inverse   ${\rm Inv_A}(z_i)$ $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Inverse \ for \ „\hspace{-0.05cm}+\hspace{0.05cm}”$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{kurz:}\hspace{0.3cm} {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}.$$

$\rm (E)$  Für jedes  $z_i$  mit Ausnahme des Nullelements existiert die multiplikative Inverse   ${\rm Inv_M}(z_i)$ $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Inverse \ for \ „\hspace{-0.05cm}\cdot\hspace{0.05cm}”$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A}, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {1}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{kurz:}\hspace{0.3cm} {\rm Inv_M}(z_i) = z_i^{-1} \hspace{0.05cm}.$$

$\rm (F)$  Für Addition und Multiplikation gilt jeweils das Kommutativgesetz $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Commutative \ Law$:

$$\forall \hspace{0.15cm} z_i,\hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + z_j = z_j + z_i ,\hspace{0.15cm}z_i \cdot z_j = z_j \cdot z_i \hspace{0.05cm}.$$

$\rm (G)$  Für Addition und Multiplikation gilt jeweils das Assoziativgesetz $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Associative \ Law$:

$$\forall \hspace{0.15cm} z_i,\hspace{0.1cm} z_j ,\hspace{0.1cm} z_k \in {\rm GF}(q)\text{:} \hspace{0.25cm}(z_i + z_j) + z_k = z_i + (z_j + z_k ),\hspace{0.15cm}(z_i \cdot z_j) \cdot z_k = z_i \cdot (z_j \cdot z_k ) \hspace{0.05cm}.$$

$\rm (H)$  Für die Kombination „Addition – Multiplikation” gilt das Distributivgesetz $\hspace{0.2cm}\Rightarrow \hspace{0.2cm}\rm Distributive \ Law$:

$$\forall \hspace{0.15cm} z_i,\hspace{0.15cm} z_j ,\hspace{0.15cm} z_k \in {\rm GF}(q)\text{:} \hspace{0.25cm}(z_i + z_j) \cdot z_k = z_i \cdot z_k + z_j \cdot z_k \hspace{0.05cm}.$$

Beispiele und Eigenschaften von Galoisfeldern

Wir überprüfen zunächst, ob für die binäre Zahlenmenge  $Z_2 = \{0, 1\}$   ⇒   $q=2$  (gültig für den einfachen Binärcode) die auf der letzten Seite genannten acht Kriterien erfüllt werden, so dass man tatsächlich von „${\rm GF}(2)$” sprechen kann. Sie sehen nachfolgend die Additions– und Multiplikationstabelle:

$$Z_2 = \{0, 1\}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c|cccccc} + & 0 & 1 \\ \hline 0 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplikation: } \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 \\ \hline 0 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right]\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm GF}(2) .$$

Man erkennt aus dieser Darstellung:

• Jedes Element der Additions– und der Multiplikationstabelle von  $Z_2$  ist wieder  $z_0 = 0$  oder  $z_0 = 1$   ⇒   das Kriterium  $\rm (A)$  ist erfüllt.
  

• Die Menge  $Z_2$  enthält das Nullelement  $(\hspace{-0.05cm}N_{\rm A} = z_0 = 0)$  und das Einselement $(\hspace{-0.05cm}N_{\rm M} = z_1 = 1)$   ⇒   die Kriterien  $\rm (B)$  und  $\rm (C)$  sind erfüllt.
  

• Die additiven Inversen  ${\rm Inv_A}(0) = 0$  und  ${\rm Inv_A}(1) = -1 \ {\rm mod}\ 2 = 1$  existieren und gehören zu  $Z_2$.
• Ebenso gibt es die multiplikative Inverse  ${\rm Inv_M}(1) = 1$   ⇒   die Kriterien  $\rm (D)$  und  $\rm (E)$  sind erfüllt.
  

• Die Gültigkeit des Kommutativgesetzes  $\rm (F)$  in der Menge  $Z_2$  erkennt man an der Symmetrie bezüglich der Tabellendiagonalen.
• Die Kriterien  $\rm (G)$  und  $\rm (H)$  werden hier ebenfalls erfüllt   ⇒   alle acht Kriterien sind erfüllt   ⇒   $Z_2 = \rm GF(2)$.
  

$\text{Beispiel 1:}$  Die Zahlenmenge  $Z_3 = \{0, 1, 2\}$   ⇒   $q = 3$  erfüllt alle acht Kriterien und ist somit ein Galoisfeld  $\rm GF(3)$:

$$Z_3 = \{0, 1, 2\}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c | cccccc} + & 0 & 1 & 2\\ \hline 0 & 0 & 1 & 2 \\ 1 & 1 & 2 & 0 \\ 2 & 2 & 0 & 1 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplikation: } \left[ \begin{array}{c | cccccc} \cdot & 0 & 1 & 2\\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 \\ 2& 0 & 2 & 1 \end{array} \right]\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm GF}(3) .$$

$\text{Beispiel 2:}$  Dagegen ist die Zahlenmenge  $Z_4 = \{0, 1, 2, 3\}$   ⇒   $q = 4$  kein Galoisfeld.

• Der Grund hierfür ist, dass es hier zum Element  $z_2 = 2$  keine multiplikative Inverse gibt. Bei einem Galoisfeld müsste nämlich gelten:   $2 \cdot {\rm Inv_M}(2) = 1$.
• In der Multiplikationstabelle gibt es aber in der dritten Zeile und dritten Spalte $($jeweils gültig für den Multiplikanden  $z_2 = 2)$  keinen Eintrag mit „$1$”.

$$Z_4 = \{0, 1, 2, 3\}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c | cccccc} + & 0 & 1 & 2 & 3\\ \hline 0 & 0 & 1 & 2 & 3\\ 1 & 1 & 2 & 3 & 0\\ 2 & 2 & 3 & 0 & 1\\ 3 & 3 & 0 & 1 & 2 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplikation: } \left[ \begin{array}{c | cccccc} \cdot& 0 & 1 & 2 & 3\\ \hline 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 1 & 2 & 3\\ 2 & 0 & 2 & 0 & 2\\ 3 & 0 & 3 & 2 & 1 \end{array} \right]\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{kein }{\rm GF}(4) .$$

$\text{Verallgemeinerung (vorerst ohne Beweis):}$

• Ein Galoisfeld  ${\rm GF}(q)$  kann in der hier beschriebenen Weise als  „Ring”  von Integergrößen modulo  $q$  nur dann gebildet werden, wenn  $q$  eine Primzahl ist:  
      $q = 2$,  $q = 3$,  $q = 5$,  $q = 7$,  $q = 11$, ...
  

• Kann man aber die Ordnung  $q$  in der Form  $q = P^m$  mit einer Primzahl  $P$  und ganzzahligem  $m$  ausdrücken, so lässt sich das Galoisfeld  ${\rm GF}(q)$  über einen  Erweiterungskörper  finden.

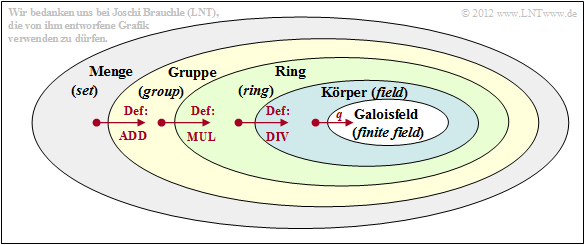
Gruppe, Ring, Körper – algebraische Grundbegriffe

Auf den ersten Seiten sind bereits einige algebraische Grundbegriffe gefallen, ohne dass deren Bedeutungen genauer erläutert wurden. Dies soll nun in aller Kürze aus Sicht eines Nachrichtentechnikers nachgeholt werden, wobei wir uns vorwiegend auf die Darstellung in  [Fri96]  und  [KM+08]  beziehen. Zusammenfassend lässt sich sagen:

$\text{Definition:}$  Ein  $\rm Galoisfeld$  ${\rm GF}(q)$ ist ein Körper  (englisch:  Field) mit einer begrenzten Anzahl  $(q)$  an Elementen   ⇒   endlicher Körper. Jeder Körper ist wieder ein Sonderfall eines Rings  (gleichlautende englische Bezeichnung), der sich selbst wieder als Spezialfall einer Abelschen Gruppe  (englisch:  Abelian Group) darstellen lässt.

Algebraische Zusammenhänge zwischen Gruppe, Ring und Körper

Die Grafik verdeutlicht schrittweise, wie sich aus einer Menge durch Definition von Additition, Multiplikation und Division innerhalb dieser Menge  $\mathcal{M}$  folgende untergeordnete Mengen ergeben:

• Abelsche Gruppe  $\mathcal{G}$  (englisch:  Field ) ,
• Ring  $\mathcal{R}$,
• Körper  $\mathcal{K}$  (englisch:  Field $\mathcal{F}$),
• endlicher Körper  $\mathcal{F}_q$  oder Galoisfeld  ${\rm GF}(q)$.

Auf den beiden nächsten Seiten werden die hier genannten algebraischen Begriffe genauer behandelt.

• Zum Verstehen der Reed–Solomon–Codes sind diese Kenntnisse allerdings nicht unbedingt erforderlich.
• Sie könnten also direkt zum Kapitel  Erweiterungskörper  springen.
  

Definition und Beispiele einer algebraischen Gruppe

Für die allgemeinen Definitionen von Gruppe (und später Ring) gehen wir von einer Menge mit unendlich vielen Elementen aus:

$$\mathcal{M} = \{\hspace{0.1cm}z_1,\hspace{0.1cm} z_2,\hspace{0.1cm} z_3 ,\hspace{0.1cm}\text{ ...} \hspace{0.1cm}\}\hspace{0.05cm}.$$

$\text{Definition:}$  Eine  $\text{algebraische Gruppe}$  $(\mathcal{G}, +)$  ist eine (beliebige) Teilmenge  $\mathcal{G} ⊂ \mathcal{M}$  zusammen mit einer zwischen allen Elementen definierten additiven Verknüpfung („$+$”), allerdings nur dann, wenn die folgenden Eigenschaften zwingend erfüllt sind:

• Für alle  $z_i, z_j ∈ \mathcal{G}$  gilt  $(z_i + z_j) ∈ \mathcal{G}$   ⇒   Closure–Kriterium für  „$+$”.
  
• Es gibt stets ein hinsichtlich der Addition neutrales Element  $N_{\rm A} ∈ \mathcal{G}$, so dass für alle  $z_i ∈ \mathcal{G}$ gilt:   $z_i +N_{\rm A} = z_i$. Bei einer Zahlengruppe ist  $N_{\rm A} \equiv 0$.
  

• Für alle  $z_i ∈ \mathcal{G}$  gibt es zudem ein hinsichtlich der Addition inverses Element  ${\rm Inv_A}(z_i) ∈ \mathcal{G}$  mit der Eigenschaft  $z_i + {\rm Inv_A}(z_i)= N_{\rm A}$.
  Bei einer Zahlengruppe ist  ${\rm Inv_A}(z_i) =- z_i$.
  

• Für alle  $z_i, z_j, z_k ∈ \mathcal{G}$  gilt:  $z_i + (z_j + z_k)= (z_i + z_j) + z_k$   ⇒   Assoziativgesetz  für  „$+$”.
  
  

Wird zusätzlich für alle  $z_i, z_j ∈ \mathcal{G}$  das Kommutativgesetz  $z_i + z_j= z_j + z_i$  erfüllt, so spricht man von einer kommutativen Gruppe  oder einer Abelschen Gruppe, benannt nach dem norwegischen Mathematiker  Niels Hendrik Abel.

$\text{Beispiele für algebraische Gruppen:}$

(1)  Die Menge der rationalen Zahlen ist definiert als die Menge aller Quotienten  $I/J$  mit ganzen Zahlen  $I$  und  $J ≠ 0$.

Diese Menge ist eine Gruppe  $(\mathcal{G}, +)$  hinsichtlich der Addition, da

• für alle  $a ∈ \mathcal{G}$  und  $b ∈ \mathcal{G}$  auch die Summe  $a+b$  wieder zu  $\mathcal{G}$  gehört,
  
• das Assozitativgesetz gilt,
  
• mit  $N_{\rm A} = 0$  das neutrale Element der Addition in  $\mathcal{G}$  enthalten ist, und
  
• es für jedes  $a$  die additive Inverse  ${\rm Inv_A}(a) = -a$  existiert.
  

Da zudem das Kommutativgesetz erfüllt ist, handelt es sich um eine Abelsche Gruppe.

(2)  Die Menge der natürlichen Zahlen   ⇒   $\{0, 1, 2, \text{...}\}$  ist hinsichtlich Addition keine algebraische Gruppe,

• da es für kein einziges Element  $z_i$  die additive Inverse  ${\rm Inv_A}(z_i) = -z_i$  gibt.
  

(3)  Die begrenzte natürliche Zahlenmenge   ⇒   $\{0, 1, 2, \text{...}\hspace{0.05cm}, q-1\}$  erfüllt dagegen dann die Bedingungen an eine Gruppe  $(\mathcal{G}, +)$,

• wenn man die Addition modulo  $q$  definiert.

(4)  Dagegen ist  $\{1, 2, 3, \text{...}\hspace{0.05cm},q\}$  keine Gruppe, da das neutrale Element der Addition  $(N_{\rm A} = 0)$  fehlt.

Definition und Beispiele eines algebraischen Rings

Entsprechend der  Übersichtsgrafik  kommt man von der Gruppe  $(\mathcal{G}, +)$  durch Definition einer zweiten Rechenoperation – der Multiplikation  („$\cdot$”)  – zum Ring  $(\mathcal{R}, +, \cdot)$. Man benötigt hierfür also neben einer Additionstabelle auch eine Multiplikationstabelle.

$\text{Definition:}$  Ein  $\text{algebraischer Ring}$  $(\mathcal{R}, +, \cdot)$ ist eine Teilmenge  $\mathcal{R} ⊂ \mathcal{G} ⊂ \mathcal{M}$  zusammen mit zwei in dieser Menge definierten Rechenoperationen, der Addition  („$+$”)  und der Multiplikation  („$·$”). Dabei müssen die folgenden Eigenschaften erfüllt werden:

• Hinsichtlich der Addition ist der Ring  $(\mathcal{R}, +, \cdot)$  eine  Abelsche Gruppe  $(\mathcal{G}, +)$.
  
• Zusätzlich gilt für alle  $z_i, z_j ∈ \mathcal{R}$  auch  $(z_i \cdot z_j) ∈ \mathcal{R}$   ⇒   Closure–Kriterium für „$\cdot$”.
  
• Es gibt stets auch ein hinsichtlich der Multiplikation neutrales Element  $N_{\rm M} ∈ \mathcal{R}$, so dass für alle  $z_i ∈ \mathcal{R}$  gilt:   $z_i \cdot N_{\rm M} = z_i$.
  Bei einer Zahlengruppe ist stets  $N_{\rm M} = 1$.
  

• Für alle  $z_i, z_j, z_k ∈ \mathcal{R}$  gilt:   $z_i + (z_j + z_k)= (z_i + z_j) + z_k$   ⇒   Assoziativgesetz  für  „$\cdot$”.
  

• Für alle  $z_i, z_j, z_k ∈ \mathcal{R}$ gilt:   $z_i \cdot (z_j + z_k) = z_i \cdot z_j + z_i \cdot z_k$   ⇒   Distributivgesetz  für  „$\cdot$”.

Weiter sollen die folgenden Vereinbarungen gelten:

• Ein Ring  $(\mathcal{R}, +, \cdot)$  ist nicht notwendigerweise kommutativ. Gilt tatsächlich auch für alle Elemente  $z_i, z_j ∈ \mathcal{R}$  das Kommutativgesetz  $z_i \cdot z_j= z_j \cdot z_i$  hinsichtlich der Multiplikation, so spricht man in der Fachliteratur von einem  kommutativen Ring.
• Existiert für jedes Element  $z_i ∈ \mathcal{R}$  mit Ausnahme von  $N_{\rm A}$  (neutrales Element der Addition, Nullelement) ein hinsichtlich der Multiplikation inverses Element  ${\rm Inv_M}(z_i)$, so dass  $z_i \cdot {\rm Inv_M}(z_i) = 1$  gilt, so liegt ein  Divisionsring  (englisch:   Division Ring) vor.
  
• Der Ring ist  nullteilerfrei  (englisch: free of zero devisors), wenn aus  $z_i \cdot z_j = 0$  zwingend  $z_i = 0$  oder  $z_j = 0$  folgt. In der abstrakten Algebra ist ein Nullteiler eines Ringes ein vom Nullelement verschiedenes Element  $z_i$, falls es ein Element  $z_j \ne 0$  gibt, so dass das Produkt  $z_i \cdot z_j = 0$  ist.
  
• Ein kommutativer nullteilerfreier Ring wird als  Integritätsring  oder  Integritätsbereich  (englisch:  Integral Domain) bezeichnet.
  
  

$\text{Fazit:}$ 

Vergleicht man die Definitionen von  Gruppe,  Ring (siehe oben), Körper  und  Galoisfeld, so erkennt man, dass ein Galoisfeld  ${\rm GF}(q)$

• ein endlicher Körper (englisch:  Field ) mit  $q$  Elementen ist,
  

• gleichzeitig als Commutative Division Ring  aufgefasst werden kann, und auch
  

• einen Integritätsbereich (englisch: Integral Domain ) beschreibt.

Aufgaben zum Kapitel

Aufgabe 2.1: Gruppe, Ring, Körper

Aufgabe 2.1Z: Welche Tabellen beschreiben Gruppen?

Aufgabe 2.2: Eigenschaften von Galoisfeldern

Aufgabe 2.2Z: Galoisfeld GF(5)