Exercise 1.2: Signal Classification
From LNTwww
Revision as of 16:52, 1 November 2020 by Oezdemir (talk | contribs) (Oezdemir moved page Aufgabe 1.2: Signalklassifizierung to Exercise 1.2: Signal Classification)
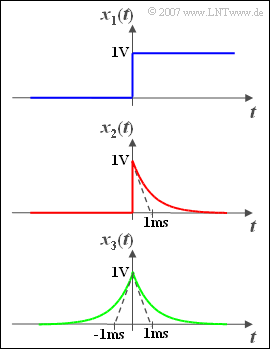
Three signal curves are shown on the Right:
- The blue signal \(x_1(t)\) is switched on at time $t = 0$ and has at $t > 0$ the value $1\,\text{V}$.
- The blue signal \(x_2(t)\) is for $t < 0$ equals zero, jumps at $t = 0$ to $1\,\text{V}$ and then falls down with the time constant $1\,\text{ms}$ . For $t > 0$ the following applies:
- \[x_2(t) = 1\,\text{V} \cdot {\rm e}^{- {t}/(1\,\text{ms})}.\]
- Correspondingly, the signal shown in green applies to all times $t$:
- \[x_3(t) = 1\,\text{V} \cdot {\rm e}^{- {|\hspace{0.05cm}t\hspace{0.05cm}|}/(1\,\text{ms})}.\]
You will now classify these three signals according to the following criteria:
- deterministic or stochastic,
- causal or acausal,
- energy limited or power limited,
- value-continuous or value-discrete,
- time-continuous or time-discrete.
Notes:
- This exercise belongs to the chapter Klassifizierung von Signalen.
Questions
Solutions
(1) The solutions 1 and 3 are applicable:
- All signals can be described completely in analytical form; therefore they are also deterministic.
- All signals are also clearly defined for all times $t$ not only at certain times. Therefore, they are always time-continuous signals.
- The signal amplitudes of \(x_2(t)\) and \(x_3(t)\) can take any values between $0$ and $1\,\text{V}$ they are therefore continuous in value.
- On the other hand, with the signal \(x_1(t)\) only the two signal values $0$ and $1\,\text{V}$ are possible; a discrete-valued signal is present.
(2) Correct are the solutions 1 and 2:
- A signal is called causal if for times $t < 0$ it does not exist or is identically zero. This applies to the signals \(x_1(t)\) and \(x_2(t)\).
- In contrast, \(x_3(t)\) belongs to the class of non-causal signals.
(3) According to the general definition:
- \[E_2=\lim_{T_{\rm M}\to\infty}\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x^2_2(t)\,\hspace{0.1cm}{\rm d}t.\]
In this case, the lower integration limit is zero and the upper integration limit $+\infty$. You get:
- \[E_2=\int^\infty_0 (1{\rm V})^2\cdot{\rm e}^{-2t/(1\rm ms)}\,\hspace{0.1cm}{\rm d}t = 5 \cdot 10^{-4}\hspace{0.1cm} \rm V^2s \hspace{0.15cm}\underline{= 0.5 \cdot 10^{-3}\hspace{0.1cm} \rm V^2s}. \]
With finite energy, the associated power is always negligible. From this follows $P_2\hspace{0.15cm}\underline{ = 0}$.
(4) Correct are the solutions 2 and 3:
- As already calculated in the last subtask, \(x_2(t)\) has a finite energy:
- $$E_2= 0.5 \cdot 10^{-3}\hspace{0.1cm} {\rm V^2s}. $$
- The energy of the signal \(x_3(t)\) is twice as large, since now the time domain $t < 0$ makes the same contribution as the time domain $t > 0$. So
- $$E_3= 10^{-3}\hspace{0.1cm} {\rm V^2s}.$$
- At signal \(x_1(t)\) the energy integral diverges: $E_1 \rightarrow \infty$. This signal has a finite power ⇒ $P_1= 0.5 \hspace{0.1cm} {\rm V}^2$.
- The result also takes into account that the signal \(x_1(t)\) in half the time $(t < 0)$ is identical to zero.
- The signal \(x_1(t)\) is accordingly power limited.