Exercise 3.8Z: Convolution of Two Rectangles

• Return to book

Zur Faltung zweier Rechtecke

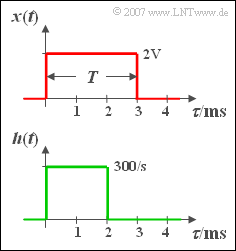
Am Eingang eines kausalen LZI-Systems (also linear und zeitinvariant) mit einer rechteckförmigen Impulsantwort  ${h(t)}$  der Dauer  $2 \,\text{ms}$  liegt ein Rechteckimpuls  ${x(t)}$  der Dauer  $T = 3 \,\text{ms}$  und der Amplitude  $A = 2\,\text{ V}$  an. Die Rechteckfunktionen beginnen jeweils zum Zeitpunkt  $t = 0$.

In dieser Aufgabe sollen Sie das Ausgangssignal  ${y(t)}$  mit Hilfe der grafischen Faltung berechnen. Wie man leicht nachprüfen kann, ist das Ausgangssignal  ${y(t)}$

• nur im Bereich von  $0$  bis  $5 \, \text{ms}$  von Null verschieden, und
• symmetrisch zum Zeitpunkt  $t = 2.5 \, \text{ms}$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Faltungssatz und Faltungsoperation.
• Sie bezieht sich vorwiegend auf die Seite  Grafische Faltung
• Die Thematik dieses Abschnitts wird auch im interaktiven Applet  Zur Verdeutlichung der grafischen Faltung veranschaulicht.

Fragebogen

1

Berechnen Sie die Signalwerte zu den Zeitpunkten  $t = 1 \,\text{ms}$  und  $t = 2 \,\text{ms}$.

$y(t = 1 \,\text{ms})\ = \ $  $\text{V}$

$y(t = 2 \,\text{ms})\ = \ $  $\text{V}$

2

Bestimmen Sie die Signalwerte für die Zeitpunkte  $t = 3 \,\text{ms}$  und  $t = 4 \,\text{ms}$  durch Ausnutzung der Symmetrieeigenschaften.

$y(t = 3 \,\text{ms})\ = \ $  $\text{V}$

$y(t = 4 \,\text{ms})\ = \ $  $\text{V}$

3

Welche der folgenden Aussagen sind zutreffend?

	Das Ausgangssignal  ${y(t)}$  hat einen trapezförmigen Verlauf.
	Das Spektrum lautet:   ${Y(f)} = Y_0 \cdot \text{si}^{2}(\pi f T)$.
	Mit  $T = 2 \,\text{ms}$  würde sich eine Dreiecksform ergeben.

Musterlösung

Solution

Zur Verdeutlichung der grafischen Faltung $x(t) \star h(t)$

(1)  Allgemein gilt für das Faltungsintegral:

$$y(t) = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot h( {t - \tau } )}\hspace{0.1cm} {\rm d}\tau.$$

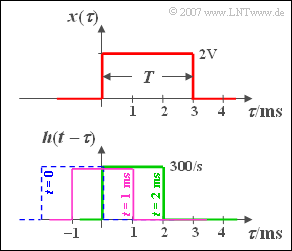
Hinweis:  Die Abszissen in nebenstehender Grafik wurden zu  $\tau$  umbenannt.

Der Signalwert zum Zeitpunkt  $t = 1 \,\text{ms}$  kann wie folgt berechnet werden:

• Spiegelung der Impulsantwort  ${h(\tau)}$,
• Verschiebung um  $t = 1 \text{ ms}$  nach rechts (violette Kurve in der Skizze),
• Multiplikation der beiden Funktionen sowie Integration.

Das Produkt ist ebenfalls rechteckförmig mit der Höhe  $2 \text{ V} \cdot 300 \; \text{1/s}$  und der Breite  $1 \,\text{ms}$. Daraus ergibt sich für die Fläche:

$$y( {t = 1\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= 0.6\;{\rm{V}}}{\rm{.}}$$

Das grüne Rechteck verdeutlicht die Berechnung des zweiten Signalwertes. Nun ist das resultierende Rechteck nach der Multiplikation doppelt so breit und man erhält:

$$y( {t = 2\;{\rm{ms}}} ) = 2\;{\rm{V}} \cdot {\rm{300}}\;{1}/{{\rm{s}}} \cdot 2\;{\rm{ms}}\hspace{0.15 cm}\underline{={\rm{1.2}}\;{\rm{V}}}{\rm{.}}$$

(2)  Wegen der Symmetrie von ${y(t)}$ bezüglich des Zeitpunktes  $t = 2.5\, \text {ms}$  gilt:

$$y( {t = 3\;{\rm{ms}}} ) = y( {t = 2\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= {\rm{1}}{\rm{.2}}\;{\rm{V}}}{\rm{,}}$$

$$y( {t = 4\;{\rm{ms}}} ) = y( {t = 1\;{\rm{ms}}} )\hspace{0.15 cm}\underline{ = 0.6\;{\rm{V}}}{\rm{.}}$$

Faltungsergebnis  $y(t)$

(3)  In den Teilaufgaben  (1)  und  (2)  wurden die Signalwerte zu diskreten Zeitpunkten berechnet.

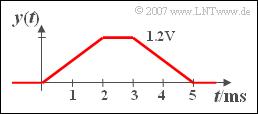
• Alle Punkte sind durch Geradenstücke zu verbinden, da die Integration über Rechteckfunktionen wachsender Breite einen linearen Verlauf ergibt.
• Das heißt:  Das Ausgangssignal  ${y(t)}$  ist trapezförmig.

• Das dazugehörige Spektrum ist komplex und lautet:

$$Y(f) = 6 \cdot 10^{ - 3} \;{{\rm{V}}}/{{{\rm{Hz}}}} \cdot {\mathop{\rm si}\nolimits} ( {2\;{\rm{ms}}\cdot{\rm{\pi }}f} ) \cdot {\mathop{\rm si}\nolimits} ( {3\;{\rm{ms}}\cdot{\rm{\pi }}f}) \cdot {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \hspace{0.05cm}\cdot \hspace{0.05cm}2.5\;{\rm{ms}}\hspace{0.05cm}\cdot \hspace{0.05cm} \pi }}f} .$$

• Hätte der Eingangsimpuls  ${x(t)}$  die Dauer  $T = 2\, \text {ms}$, so würde  ${y(t)}$  einen dreieckförmigen Signalverlauf zwischen  ${t = 0}$  und  $t = 4 \text { ms}$  zeigen.
• Das Maximum  $1.2 \, \text {V}$  ergäbe sich dann nur zum Zeitpunkt  $t = 2 \, \text {ms}$.

Richtig sind somit die Lösungsvorschläge 1 und 3.