Exercise 5.2Z: DFT of a Triangular Pulse
Betrachtet wird der skizzierte Dreieckimpuls
- $$x(t) = \left\{ \begin{array}{l} A \cdot \left( 1 - {|t|}/{T} \right ) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| \le T,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > T.} \\ \end{array}$$
Die Signalparameter haben folgende Werte:
- Amplitude $A = 4 \ \text{V}$,
- äquivalente Impulsdauer $\Delta t = T = 1 \, \text{ms}$.
Das Spektrum $X(f)$ erhält man durch Anwendung des ersten Fourierintegrals:
- $$X(f) = A \cdot T \cdot {\rm si}^2(\pi f T)\hspace{0.05cm}.$$
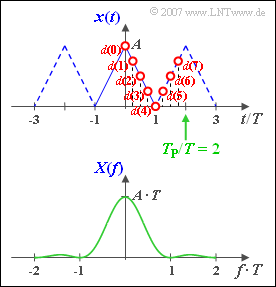
Die Spektralfunktion soll nun durch eine Diskrete Fouriertransformation (DFT) mit $N = 8$ angenähert werden, wobei die $N$ Koeffizienten für den Zeitbereich ⇒ $d(0)$, ... , $d(7)$ der Grafik entnommen werden können.
Die dazugehörigen Spektralkoeffizienten $D(0)$, ... , $D(7)$ sind zu ermitteln, wobei für die Indizes $\mu = 0$, ... , $N–1$ gilt:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Bezeichnet man den Abstand zweier Abtastwerte im Zeitbereich mit $T_{\rm A}$ und den entsprechenden Frequenzabstand zweier Linien mit $f_{\rm A}$, so gilt folgender Zusammenhang:
- $$N \cdot f_{\rm A} \cdot T_{\rm A} = 1 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Diskrete Fouriertransformation (DFT).
- Ihre Lösungen können Sie mit dem interaktiven Applet Diskrete Fouriertransformation und Inverse überrprüfen.
Fragebogen
Musterlösung
- $${d(0) = 4\,{\rm V}, \hspace{0.1cm}d(1) = d(7) = 3\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(2) = d(6) = 2\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(3) = d(5) = 1\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(4) = 0}\hspace{0.05cm}. $$
- $$\Rightarrow \hspace{0.15 cm}\underline{d(0) = 4\,{\rm V}, \hspace{0.1cm}d(3) = 1\,{\rm V}, \hspace{0.1cm}d(6) = 2\,{\rm V}. \hspace{0.1cm}} \hspace{0.05cm} $$
(2) Entsprechend der Grafik gilt $T_{\rm A} = T/4$.
- Mit $T = 1 \ \text{ms}$ erhält man somit $\underline{T_{\rm A} = 0.25 \ \text{ms}}$.
(3) Für die Abstände der Abtastwerte im Zeit– und Frequenzbereich gilt:
- $$N \cdot f_{\rm A} \cdot T_{\rm A} = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A}= \frac{1}{ 8 \cdot 0.25\, {\rm ms}}\hspace{0.15 cm}\underline{= 0.5\, {\rm kHz}}\hspace{0.05cm}.$$
(4) Mit $N = 8$ und $\mu = 0$ folgt aus der DFT–Gleichung:
- $$D(0) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu) = \frac{1\,{\rm V}}{8}\cdot (4+3+2+1+0+1+2+3)\hspace{0.15 cm}\underline{= 2 \,{\rm V}}\hspace{0.05cm}.$$
- Der DFT–Wert $D(0)$ beschreibt den Spektralwert bei $f = 0$, wobei folgender Zusammenhang gilt:
- $$X(f=0) = \frac{D(0)}{f_{\rm A}}= \frac{ 2\,{\rm V}}{0.5\,{\rm kHz}}= 4 \cdot 10^{-3}\,{\rm V/Hz}\hspace{0.05cm}.$$
- Dieser Wert stimmt mit dem theoretischen Wert $(A \cdot T)$ überein.
(5) Mit $N = 8$ und $\mu = 2$ erhält man:
- $$D(2) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot (-{\rm j})^{\nu} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} = \frac{1\,{\rm V}}{8}\cdot (4-3\cdot{\rm j}-2+{\rm j}-{\rm j}-2+3\cdot{\rm j})\hspace{0.15 cm}\underline{= 0}\hspace{0.05cm}.$$
Dieses Ergebnis hätte man auch ohne Rechnung vorhersagen können:
- Die DFT-Koeffizienten $D(\mu)$ sind gleichzeitig die Fourierkoeffizienten der im Abstand $T_{\rm P} = 2T$ periodifizierten Funktion $x_{\rm Per}(t)$. Diese ist in der Grafik auf der Angabenseite gestrichelt eingezeichnet.
- Aufgrund von Symmetrieeigenschaften sind aber alle geradzahligen Fourierkoeffizienten der Funktion $x_{\rm Per}(t)$ gleich Null: ⇒ $D(4)\hspace{0.15cm}\underline{=0},$ $D(6)\hspace{0.15cm}\underline{=0}$.
(6) Der Koeffizient $D(7)$ beschreibt die periodifizierte Spektralfunktion bei der Frequenz $f = 7 \cdot f_{\rm A}$. Aufgrund der Periodizität und von Symmetrieeigenschaft gilt:
- $$D(7) = D(-1) = D^{\star}(1) \hspace{0.05cm}.$$
Vorzugsweise berechnen wir diesen DFT–Koeffizienten:
- $$D(1) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \frac{1\,{\rm V}}{8}\cdot \left(4 +3\cdot \frac{1 - {\rm j}}{\sqrt{2}}-2\cdot {\rm j}+ \frac{-1 - {\rm j}}{\sqrt{2}}-{\rm j}+ \frac{-1 + {\rm j}}{\sqrt{2}}-{\rm j}+ 2\cdot {\rm j}+3\cdot \frac{1 - {\rm j}}{\sqrt{2}}\right)$$
- $$\Rightarrow \; \; D(1) = \frac{2 + \sqrt{2}}{4} \approx 0.854{\rm V}\hspace{0.05cm}.$$
Da $D(1)$ rein reell ist, gilt $D(7) = D(1) \; \underline{= 0.854 \ {\rm V}}$.
Daraus ergeben sich für die zugehörigen Werte der kontinuierlichen Spektralfunktion:
- $$X(f=-f_{\rm A}) = X(f=+f_{\rm A}) =\frac{D(1)}{f_{\rm A}}= 1.708 \cdot 10^{-3}\,{\rm V/Hz}\hspace{0.05cm}.$$
- Wegen der impliziten periodischen Fortsetzung durch die DFT stimmt der so berechnete Wert mit dem tatsächlichen Wert $(4 \cdot A \cdot T/\pi^2 = 1.621 · 10^{-3}\text{ V/Hz})$ nicht exakt überein.
- Der relative Fehler beträgt ca. $5.3\%$.