Exercise 2.6: Dimensions in GWSSUS
From LNTwww
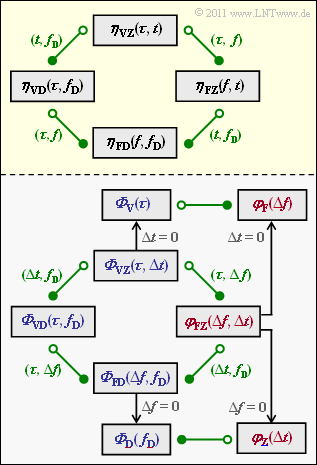
The mobile radio channel can be described in very general terms by four system functions, whereby the relationship between each pair of functions is described by
- the Fourier transform or
- the inverse Fourier transform.
We denote all of the functions with $\eta_{i_1i_2}$. The indices $i_1$ and $i_2$ are defined as follows:
- V stands for delay $\tau$ (index $i_1$),
- F stands for frequency $f$ (index $i_1$),
- Z stands for the time $t$ (index $i_2$)
- D stands for the Doppler frequency $f_{\rm D}$ (index $i_2$).
The relationship between the functions is shown in the diagram (yellow background). The Fourier correspondences are shown in green:
- The transition from a circle filled with white to a circle filled with green corresponds to a Fourier transform.
- The transition from a circle filled with green to a circle filled with white corresponds to the inverse Fourier transform (opposite direction).
For example:
- $$\eta_{\rm VZ}(\tau, t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.02cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,t)\hspace{0.05cm}, \hspace{0.4cm}\eta_{\rm FZ}(f,t) \hspace{0.2cm} \stackrel{f, \hspace{0.02cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.05cm}.$$
- The correlation function $\varphi_{i_1i_2}$ and the power density spectrum $\it \Phi_{i_1i_2}$ are provided with the same indices as the system function $\eta_{i_1i_2}$.
- Correlation functions can be recognized by the red font in the lower graph and all power spectral densities are labeled in blue. The GWSSUS model is always assumed.
Let us consider here the system function $\eta_{\rm VZ}(\tau, t)$, i.e. the time variant impulse response $h(\tau, t)$. We define:
- $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$
- $$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VZ}(\Delta \tau, \Delta t) \hspace{0.05cm}, $$
- $$\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.$$
- $${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)\hspace{0.05cm}. $$
Note: This task belongs to the chapter Das GWSUS–Kanalmodell.
Questionnaire
Sample solution
(1) All statements are correct:
- $\eta_{\rm VZ}(\tau, t)$ is the time-variant impulse response, for which the term $h(\tau, t)$ is also common. Like every impulse response, $h(\tau, t)$ has the unit $[1/\rm s]$.
- By Fourier transformation of the function $\eta_{\rm VZ}(\tau, t)$ with respect to the delay $\tau$ one obtains
- $$\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}. $$
- Due to the integration over $\tau$ (unit: $\rm s$), the time-variant transfer function $\eta_{\rm FZ}(f, t)$ is dimensionless. In some literature, $H(f, t)$ is also used instead of $\eta_{\rm FZ}(f, t)$.
- The delay–Doppler representation $\eta_{\rm VD}(\tau, f_{\rm D})$ is also dimensionless. This function results from the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ by Fourier transformation with respect to $t$:
- $$\eta_{\rm VD}(\tau, f_{\rm D}) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}t \hspace{0.05cm}.$$
- The function $\eta_{\rm FD}(t, f_{\rm D})$ is obtained from the dimensionless functions $\eta_{\rm VD}(\tau, f_{\rm D})$ and $\eta_{\rm FZ}(f, t)$ respectively by a Fourier transformation, which results in the unit $[\rm s] = [1/\rm Hz]$.
(2) Solutions 2 and 3 are correct:
- The autocorrelation (ACF) function is by definition the following expected value:
- $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm}.$$
- Since the time-variant impulse response $\eta_{\rm VZ}(\tau, t)$ has the unit $[1/\rm s]$, its ACF $\varphi_{\rm VZ}$ has the unit $[1/\rm s^2]$, both in the general case $\varphi_{\rm VZ}(\tau_1, l_1, \tau_2, t_2)$ and with the GWSSUS case $\varphi_{\rm VZ}(\delta \tau, \ \delta t)$.
- The Dirac function $\delta(\Delta \tau)$ has the dimension $[1/\rm s]$, since the integral over all $\tau$ (with dimension $[\rm s]$) must be $1$. Therefore, both the delay–time cross power density spectrum ${\it \Phi}_{\rm VZ}(\tau, \delta \tau)$ and the delay power density spectrum ${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \delta t = 0)$ have dimension $[1/\rm s]$.
(3) Statements 1 and 3 are correct:
- The function ${\it \Phi}_{\rm VZ}(\tau, \delta t)$ has dimension $[1/\rm s]$. Its Fourier transform with respect to $\tau$ is $\varphi_{\rm FZ}(\Delta f, \Delta t)$, while its Fourier transform with respect to $t$ is ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$. Both $\varphi_{\rm FZ}(\Delta f, \Delta t)$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ are therefore dimensionless.
- The frequency–Doppler cross power density spectrum has the unit $[\rm s] = [1/\rm Hz]$, because
- $${\it \Phi}_{\rm FD}(\delta f, f_{\rm D}) = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}. $$