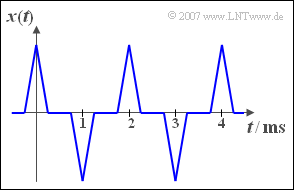
Exercise 2.1: Rectification

• Return to book

Periodisches Dreiecksignal

The graph shows the periodic signal  $x(t)$. If  $x(t)$ is applied to the input of a non-linearity with the characteristic curve

$$y=g(x)=\left\{ {x \; \rm f\ddot{u}r\; \it x \geq \rm 0, \atop {\rm 0 \;\;\; \rm sonst,}}\right.$$

the signall  $y(t)$ is obtained at the output. A second non-linear characteristic

$$z=h(x)=|x|$$

delivers the signal  $z(t)$.

Hint:

• This exercise belongs to the chapter  General description of periodic signals.

Questions

1

Which of the following statements are true?

	$y = g(x)$  beschreibt einen Einweggleichrichter.
	$y = g(x)$  beschreibt einen Zweiweggleichrichter.
	$z = h(x)$  beschreibt einen Einweggleichrichter.
	$z = h(x)$  beschreibt einen Zweiweggleichrichter

2

Wie groß ist die Grundfrequenz $f_0$  des Signals  $x(t)$?

$f_0 \ = \ $   $\text{Hz}$

3

Wie groß ist die Periodendauer  $T_0$  des Signals  $y(t)$?

$T_0 \ = \ $   $\text{ms}$

4

Wie groß ist die Grundkreisfrequenz  $\omega_0$  des Signals  $z(t)$?

$\omega_0 \ = \ $   $\text{1/s}$

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1 und 4:

• Die nichtlineare Kennlinie  $y = g(x)$  beschreibt einen Einweggleichrichter.
• $z = h(x) = |x|$  beschreibt einen Zweiweggleichrichter.

(2)  Die Periodendauer des gegebenen Signals  $x(t)$  beträgt  $T_0 = 2\,\text{ms}$. Der Kehrwert hiervon ergibt die Grundfrequenz  $f_0 \hspace{0.1cm}\underline{ = 500\,\text{Hz}}$.

(3)  Die Einweggleichrichtung ändert nichts an der Periodendauer, siehe linke Skizze. Somit gilt weiterhin  $T_0 \hspace{0.1cm}\underline{= 2\,\text{ms}}$.

Periodische Dreiecksignale

(4)  Das Signal  $z(t)$  nach der Doppelweggleichrichtung hat dagegen die doppelte Frequenz (siehe rechte Darstellung). Hier gelten folgende Werte:

$$T_0 = 1\,\text{ms}, \hspace{0.5cm} f_0 = 1\,\text{kHz}, \hspace{0.5cm} \omega_0 \hspace{0.1cm}\underline{= 6283\,\text{1/s}}.$$