Exercise 2.3: Cosine and Sine Components

Spektrum von Cosinus- und Sinusanteilen

Given is the amplitude spectrum $X(f)$ of a signal $x(t)$ according to the graph.

Let $f_1 = 4\,\text{kHz}$ be the normalisation frequency.
Thus the actual frequencies of the signal components are $0\,\text{kHz}$, $4\,\text{kHz}$ and $10\,\text{kHz}$.

This signal $x(t)$ is at the input of a linear differentiator whose output can be represented with $\omega_1 = 2\pi f_1$ as follows:

$$y(t)=\frac{1}{\omega_1}\cdot\frac{ {\rm d} x(t)}{{\rm d} t}.$$

Hint:

This exercise belongs to the chapter Harmonic Oscillation.

Questions

$x(t=0)\ = \ $

${\rm V}$

$T_0\ = \ $

${\rm ms}$

$y(t=0)\ = \ $

${\rm V}$

	$y(t)$ has the same period duration as the signal $x(t)$.
	$Y(f)$ contains a Dirac function at the frequency $f = 0$.
	$Y(f)$ contains a Dirac function at $+f_1$ with weight $\rm{j} · 1\,{\rm V}$.
	$Y(f)$ contains a Dirac function at $–\hspace{-0.1cm}2.5 \cdot f_1$ with weight $5\,{\rm V}$.

Solution

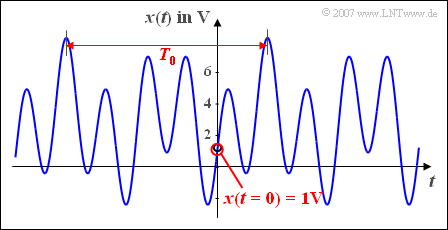
Summensignal aus Cosinus- und Sinusanteilen

(1) The time signal has the following form:

$$x(t)={\rm 3V}-{\rm 2V}\cdot \cos(\omega_{\rm 1} \cdot t)+{\rm 4V} \cdot \sin(2.5 \cdot \omega_{\rm 1} \cdot t).$$

Here $\omega_1 = 2\pi f_1$ denotes the angular frequency of the cosine component.
At time $t = 0$ the signal has the value $x(t=0)\hspace{0.15 cm}\underline{=1\,\rm V}$.

(2) The base frequency $f_0$ is the least common divisor

of $f_1 = 4{\,\rm kHz}$
and $2.5 · f_1 = 10{\,\rm kHz}$.

From this follows $f_0 = 2{\,\rm kHz}$ ⇒ period duration $T_0 = 1/f_0 \hspace{0.1cm}\underline{= 0.5 {\,\rm ms}}$.

Spektrum mit diskreten Anteilen

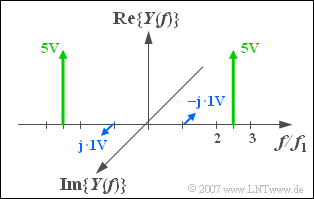
(3) The following applies to the output signal $y(t)$ of the differentiatior:

$$y(t)=\frac{1}{\omega_1}\cdot\frac{ {\rm d}x(t)}{{\rm d}t}=\frac{ {\rm -2V}}{\omega_1}\cdot\omega_1 \cdot (-\sin(\omega_1 t))+\frac{\rm 4V}{\omega_1}\cdot 2.5\omega_1\cdot {\rm cos}(2.5\omega_1t).$$

This leads to the solution:

$$y(t)={\rm 2V}\cdot\sin(\omega_1 t)+{\rm 10V}\cdot\cos(2.5\omega_1 t).$$

For $t = 0$ the value $y(t=0)\hspace{0.15cm}\underline{=10\,\rm V}$ follows.
The spectrum $Y(f)$ is shown on the right.

(4) The solutions 1 and 4 are correct:

The period duration $T_0$ is not changed by the amplitude and phase of the two components.
This means, that $T_0 = 0.5 {\,\rm ms}$ still applies.
The DC component disappears due to the differentiation.
The component $f_1$ is sinusoidal. Thus $X(f)$ has an (imaginary) Dirac at $f = f_1$, but with a negative sign.
The cosine component with amplitude ${10\,\rm V}$ results in the two Dirac functions at $\pm 2.5 \cdot f_1$ , each with weight ${5\,\rm V}$ .