Complementary Gaussian Error Functions

Open Applet in a new tab     Hinweis:   Das Applet ist für den CHROME–Browser optimiert. Bei anderen Browsern kommt es teilweise zu Darstellungsproblemen.

Applet Description

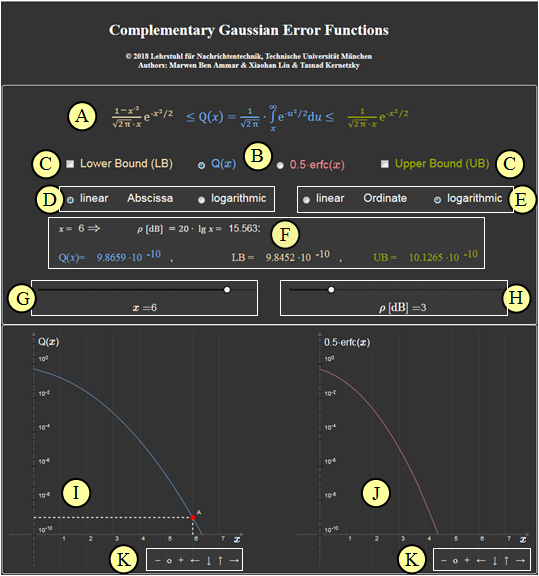
This applet allows the calculation and graphical representation of the (complementary) Gaussian error functions  ${\rm Q}(x)$  and  $1/2\cdot {\rm erfc}(x)$, which are of great importance for error probability calculation.

• Both the abscissa and the function value can be represented either linearly or logarithmically.
• For both functions an upper bound  $\rm (UB)$  and a lower bound  $\rm (LB)$  are given.

Theoretical Background

In the study of digital transmission systems, it is often necessary to determine the probability that a (mean-free) Gaussian distributed random variable  $x$  with variance  $σ^2$  exceeds a given value  $x_0$.  For this probability holds:

$${\rm Pr}(x > x_0)={\rm Q}(\frac{x_0}{\sigma}) = 1/2 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$

The function ${\rm Q}(x )$

The function  ${\rm Q}(x)$  is called the  complementary Gaussian error integral.  The following calculation rule applies:

$${\rm Q}(x ) = \frac{1}{\sqrt{2\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}/\hspace{0.05cm} 2}\,{\rm d} u .$$

• This integral cannot be solved analytically and must be taken from tables if one does not have this applet available.
• Specially for larger  $x$  values  (i.e., for small error probabilities), the bounds given below provide a useful estimate for  ${\rm Q}(x)$, which can also be calculated without tables.
• An upper bound  $\rm (UB)$  of this function is:

$${\rm Q}_{\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ] = \frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x).$$

• Correspondingly, for the lower bound  $\rm (LB)$:

$${\rm Q}_{\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ] =\frac{1-1/x^2}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{-x^ 2/\hspace{0.05cm}2} ={\rm Q}_{\rm UB}(x ) \cdot (1-1/x^2)< {\rm Q}(x).$$

However, in many program libraries, the function  ${\rm Q}(x )$  cannot be found.

The function $1/2 \cdot {\rm erfc}(x )$

On the other hand, in almost all program libraries, you can find the  Complementary Gaussian Error Function:

$${\rm erfc}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u ,$$

which is related to  ${\rm Q}(x)$  as follows:   ${\rm Q}(x)=1/2\cdot {\rm erfc}(x/{\sqrt{2}}).$

• Since in almost all applications this function is used with the factor  $1/2$, in this applet exactly this function was realized:

$$1/2 \cdot{\rm erfc}(x) = \frac{1}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$

• Once again, an upper and lower bound can be specified for this function:

$$\text{Upper Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ 1}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} ,$$

$$\text{Lower Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ {1-1/(2x^2)}}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} .$$

When which function offers advantages?

$\text{Example 1:}$  We consider binary baseband transmission. Here, the bit error probability  $p_{\rm B} = {\rm Q}({s_0}/{\sigma_d})$, where the useful signal can take the values  $\pm s_0$  and the noise root mean square value  $\sigma_d$ .

It is assumed that tables are available listing the argument of the two Gaussian error functions at distance  $0.1$.  With  $s_0/\sigma_d = 4$  one obtains for the bit error probability according to the function  ${\rm Q}(x )$:

$$p_{\rm B} = {\rm Q} (4) \approx 0.317 \cdot 10^{-4}\hspace{0.05cm}.$$

According to the second equation, we get:

$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2} })= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.$$

• The first value is more correct.  In the second method of calculation, one must round or – even better – interpolate, which is very difficult due to the strong nonlinearity of this function.
  
• Accordingly, with the given numerical values, ${\rm Q}(x )$  is more suitable.  However, outside of exercise examples  $s_0/\sigma_d$  will usually have a „curvilinear” value.  In this case, of course,  ${\rm Q}(x)$  offers no advantage over  $1/2 \cdot{\rm erfc}(x)$.

$\text{Example 2:}$  With the energy per bit  $(E_{\rm B})$  and the noise power density  $(N_0)$  the bit error probability of Binary Phase Shift Keying  (BPSK) is:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2 E_{\rm B} }/{N_0} }\right ) = {1}/{2} \cdot { \rm erfc} \left ( \sqrt{ {E_{\rm B} }/{N_0} }\right ) \hspace{0.05cm}.$$

For the numerical values  $E_{\rm B} = 16 \rm mWs$  and  $N_0 = 16 \rm mW/Hz$  we obtain:

$$p_{\rm B} = {\rm Q} \left (4 \cdot \sqrt{ 2} \right ) = {1}/{2} \cdot {\rm erfc} \left ( 4\right ) \hspace{0.05cm}.$$

• The first way leads to the result  $p_{\rm B} = {\rm Q} (5.657) \approx {\rm Q} (5.7) = 0.6 \cdot 10^{-8}\hspace{0.01cm}$, while   $1/2 \cdot{\rm erfc}(x)$  here the more correct value  $p_{\rm B} \approx 0.771 \cdot 10^{-8}$  yields.
• As in the first example, however, you can see:   The functions  ${\rm Q}(x)$  and  $1/2 \cdot{\rm erfc}(x)$  are basically equally well suited.
• Advantages or disadvantages of one or the other function arise only for concrete numerical values.

Exercises

• First select the number  $(1, 2, \text{...})$  of the exercise.  The number  $0$  corresponds to a "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values ​​are adjusted.  Solution after pressing "Show solution".
  

(1)   Find the values of the function  ${\rm Q}(x)$  for  $x=1$,  $x=2$,  $x=4$  and  $x=6$.  Interpret the graphs at linear and logarithmic ordinates.

• The applet returns the values  ${\rm Q}(1)=1.5866 \cdot 10^{-1}$,  ${\rm Q}(2)=2. 275 \cdot 10^{-2}$,  ${\rm Q}(4)=3.1671 \cdot 10^{-5}$  and  ${\rm Q}(6)=9.8659 \cdot 10^{-10}$.
• With linear ordinate, the values for  $x>3$  are indistinguishable from the zero line.  More interesting is the plot with logarithmic ordinate.

(2)   Evaluate the two bounds  ${\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ]$  and  ${\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ]$  for the  ${\rm Q}$  function.

• For  $x \ge 2$  the upper bound is only slightly above  ${\rm Q}(x)$  and the lower bound is only slightly below  ${\rm Q}(x)$. 
• For example:  ${\rm Q}(x=4)=3.1671 \cdot 10^{-5}$   ⇒   ${\rm LB}(x=4)=3.1366 \cdot 10^{-5}$,   ${\rm UB}(x=4)=3.3458 \cdot 10^{-5}$.
• The upper bound has greater significance for assessing a communications system than "LB",  since this corresponds to a "worst case" consideration.

(3)   Try to use the app to determine  ${\rm Q}(x=2 \cdot \sqrt{2} \approx 2.828)$  as accurately as possible despite the quantization of the input parameter.

• The program returns for  $x=2.8$  the too large result  $2.5551 \cdot 10^{-3}$  and for  $x=2.85$  the result  $2.186 \cdot 10^{-3}$.  The exact value lies in between.
• But it also holds:  ${\rm Q}(x=2 \cdot \sqrt{2})=0.5 \cdot {\rm erfc}(x=2)$.  This gives the exact value  ${\rm Q}(x=2 \cdot \sqrt{2})=2.3389 \cdot 10^{-3}$.

(4)   Find the values of the function  $0.5 \cdot {\rm erfc}(x)$  for  $x=1$,  $x=2$,  $x=3$  and  $x=4$.  Interpret the exact results and the bounds.

• The applet returns:  $0.5 \cdot {\rm erfc}(1)=7.865 \cdot 10^{-2}$,  $0.5 \cdot {\rm erfc}(2)=2. 3389 \cdot 10^{-3}$,  $0.5 \cdot {\rm erfc}(3)=1.1045 \cdot 10^{-5}$  and  $0.5 \cdot {\rm erfc}(4)=7.7086 \cdot 10^{-9}$.
• All the above statements about  ${\rm Q}(x)$  with respect to suitable representation type and upper and lower bounds also apply to the function  $0.5 \cdot {\rm erfc}(x)$.

(5)   The results of  (4)  are now to be converted for the case of a logarithmic abscissa.  The conversion is done accordingly  $\rho\big[{\rm dB}\big ] = 20 \cdot \lg(x)$.

• The linear abscissa value  $x=1$  leads to the logarithmic abscissa value  $\rho=0\ \rm dB$   ⇒   $0. 5 \cdot {\rm erfc}(\rho=0\ {\rm dB})={0.5 \cdot \rm erfc}(x=1)=7.865 \cdot 10^{-2}$.
• Similarly  $0.5 \cdot {\rm erfc}(\rho=6.021\ {\rm dB}) =0.5 \cdot {\rm erfc}(x=2)=2. 3389 \cdot 10^{-3}$,     $0.5 \cdot {\rm erfc}(\rho=9.542\ {\rm dB})=0.5 \cdot {\rm erfc}(3)=1.1045 \cdot 10^{-5}$,   
• $0.5 \cdot {\rm erfc}(\rho=12.041\ {\rm dB})= 0.5 \cdot {\rm erfc}(4)=7.7086 \cdot 10^{-9}$.
• As per right diagram:  $0.5 \cdot {\rm erfc}(\rho=6\ {\rm dB}) =2.3883 \cdot 10^{-3}$,     $0.5 \cdot {\rm erfc}(\rho=9. 5\ {\rm dB}) =1.2109 \cdot 10^{-5}$,     $0.5 \cdot {\rm erfc}(\rho=12\ {\rm dB}) =9.006 \cdot 10^{-9}$.

(6)   Find  ${\rm Q}(\rho=0\ {\rm dB})$,  ${\rm Q}(\rho=5\ {\rm dB})$  and  ${\rm Q}(\rho=10\ {\rm dB})$,  and establish the relationship between linear and logarithmic abscissa.

• The program returns for logarithmic abscissa  ${\rm Q}(\rho=0\ {\rm dB})=1. 5866 \cdot 10^{-1}$,  ${\rm Q}(\rho=5\ {\rm dB})=3.7679 \cdot 10^{-2}$,  ${\rm Q}(\rho=10\ {\rm dB})=7.827 \cdot 10^{-4}$.
• The conversion is done according to the equation  $x=10^{\hspace{0.05cm}0.05\hspace{0.05cm} \cdot\hspace{0.05cm} \rho[{\rm dB}]}$.  For  $\rho=0\ {\rm dB}$  we get  $x=1$   ⇒   ${\rm Q}(\rho=0\ {\rm dB})={\rm Q}(x=1) =1.5866 \cdot 10^{-1}$.
• For  $\rho=5\ {\rm dB}$  we get  $x=1.1778$   ⇒   ${\rm Q}(\rho=5\ {\rm dB})={\rm Q}(x=1. 778) =3.7679 \cdot 10^{-2}$.  From the left diagram:  ${\rm Q}(x=1.8) =3.593 \cdot 10^{-2}$.
• For  $\rho=10\ {\rm dB}$  we get  $x=3.162$   ⇒   ${\rm Q}(\rho=10\ {\rm dB})={\rm Q}(x=3. 162) =7.827 \cdot 10^{-4}$.  After „quantization”:  ${\rm Q}(x=3.15) =8.1635 \cdot 10^{-4}$.

Applet Manual

    (A)     Verwendete Gleichungen am Beispiel  ${\rm Q}(x)$

    (B)     Auswahloption für  ${\rm Q}(x)$  oder  ${\rm 0.5 \cdot erfc}(x)$

    (C)     Schranken  ${\rm LB}$  und  ${\rm UB}$  werden gezeichnet

    (D)     Auswahl, ob Abszisse linear  $\rm (lin)$  oder logarithmisch  $\rm (log)$ 

    (E)     Auswahl, ob Ordinate linear  $\rm (lin)$  oder logarithmisch  $\rm (log)$ 

    (F)     Numerikausgabe am Beispiel  ${\rm Q}(x)$  bei linearer Abszisse

    (G)     Slidereingabe des Abszissenwertes  $x$  für lineare Abszisse

    (H)     Slidereingabe des Abszissenwertes  $\rho \ \rm [dB]$  für logarithmische Abszisse

    (I)     Grafikausgabe der Funktion  ${\rm Q}(x)$  – hier:  lineare Abszisse

    (J)     Grafikausgabe der Funktion  ${\rm 0.5 \cdot erfc}(x)$  – hier:  lineare Abszisse

    (K)     Variationsmöglichkeit für die graphischen Darstellungen

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2007 by  Thomas Großer  as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
• In 2018 the program was redesigned by  Xiaohan Liu  as part of her bachelor thesis  (Supervisor: Tasnád Kernetzky ) via „HTML5”.
• Last revision and English version 2021 by  Carolin Mirschina  in the context of a working student activity.  Translation using DEEPL.com.

The conversion of this applet to HTML 5 was financially supported by  "Studienzuschüsse"  (Faculty EI of the TU Munich).  We thank.

Once again: Open Applet in new Tab

Open Applet in a new tab     Hinweis:   Das Applet ist für CHROME–Browser optimiert. Bei anderen Browsern kommt es teilweise zu Darstellungsproblemen.