Exercise 2.5Z: Square Wave

Verschiedene Rechtecksignale

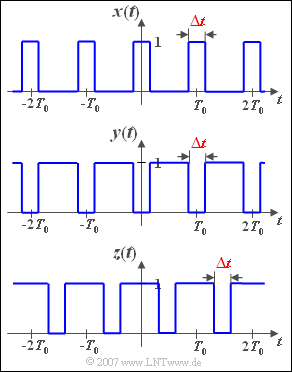
The signal $x(t)$ periodic with time $T_0$ is described by the single parameter $\Delta t$ ; let the amplitude of the square-wave pulses be $1$ in each case. Since $x(t)$ is even, all sine coefficients $B_n = 0$.

The DC signal coefficient is $A_0 = \Delta t/T_0$ and the following applies to the cosine coefficients:

$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$

In subtasks (1) and (2) the signal $x(t)$ is analysed for the two parameter values $\Delta t/T_0 = 0.5$ and $\Delta t/T_0 = 0.25$ respectively.

Then we consider the two signals $y(t)$ and $z(t)$, each with $\Delta t/T_0 = 0.25$. There is a fixed relationship between these signals and $x(t)$ which can be exploited for the calculation.

Hints:

This exercise belongs to the chapter Fourier Series.
You can find a compact summary of the topic in the two learning videos

Zur Berechnung der Fourierkoeffizienten,

Eigenschaften der Fourierreihendarstellung.

Questions

	The spectral function ${X(f)}$ contains a Dirac function at $f = 0$ with the weight $0.5$.
	The spectral function ${X(f)}$ contains Dirac lines at all multiples of the base frequency $f_0 = 1/T_0$.
	The spectral function ${X(f)}$ contains diraclines at odd multiples of the base frequency $f_0$.
	The spectral line at $f_0$ has the weight $2/\pi = 0.636$.
	The spectral line at $–\hspace{-0.1cm}f_0$ has the weight $1/\pi = 0.318$.

	The spectral function ${X(f)}$ contains diraclines at all odd multiples of the base frequency $f_0$.
	${X(f)}$ has diraclines at $\pm2f_0$, $\pm6f_0$, $\pm10f_0$, etc.
	${X(f)}$ has diraclines at $\pm4f_0$, $\pm8f_0$, $\pm12f_0$, etc.
	The spectral line at $2f_0$ has the weight $1/(2\pi) = 0.159$.

$y(t)$: $A_0 \ = \ $

$y(t)$: $A_1\ = \ $

$\hspace{1cm}A_2 \ = \ $

$z(t)$: $A_1 \ = \ $

$\hspace{1cm}A_2 \ = \ $

Solution

(1) Statements 1, 3 and 5 are correct:

The spectral function contains a Dirac function at $f = 0$ with the weight $0.5$ (DC component) as well as further spectral lines at odd multiples ($n = \pm1, \pm3, \pm5,\text{...}$ of $f_0$.

The weights at $\pm f_0$ are $A_1/2 = 1/\pi = 0.318$ in each case.

(2) Statements 1, 2 and 4 are correct:

Spectral lines exist at all odd multiples of the fundamental frequency, and additionally at the $2–{\rm fold}$, $6–{\rm fold}$ and $10–{\rm fold}$.
For example $A_1 = 1/\pi = 0.450$. The spectral line at $2f_0$ thus has the weight $A_2/2 = 1/(2\pi) = 0.159$.
For $n = 4$, $n = 8$, etc., on the other hand, the coefficients $A_n = 0$, since the following holds for the sine function: $\sin(\pi) = \sin(2\pi) =\text{ ...} = 0$.

(3) From the graphical representation of the signal ${y(t)}$ it is clear that $A_0 = 0.75$ must apply. The same result can be obtained using the relationship:

$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$

(4) The following applies: ${y(t)} = 1 - x(t)$. For $n \neq 0$ the Fourier coefficients are the same as for the signal $x(t)$, but with negative signs. In particular:

$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$

$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$

(5) ${z(t)} = y(t - T_0/2)$ applies. With the Fourier series representation of ${y(t)}$ it follows:

$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$

$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$

Thus one obtains:

$$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$

he same result is obtained starting from the given coefficients with $\Delta t/T_0 = 0.75$:

$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$