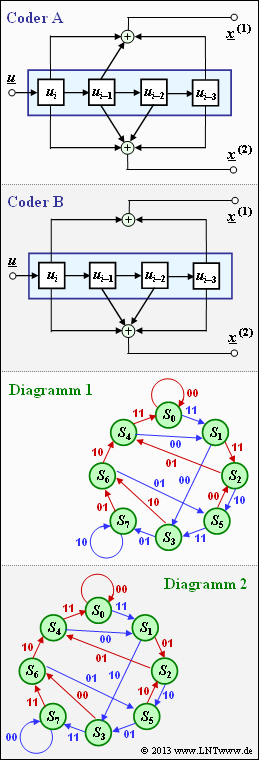
Exercise 3.7Z: Which Code is Catastrophic?
From LNTwww
Codierer für $m = 3$ und Zustandsübergangsdiagramm
Die nebenstehende Grafik zeigt
- zwei unterschiedliche $\text{ Coder A }$ und $\text{ Coder B}$, jeweils mit dem Gedächtnis $m = 3$ (oben),
- zwei Zustandsübergangsdiagramme, bezeichnet mit $\text{ Diagramm 1 }$ und $\text{ Diagramm 2 }$ (unten).
In der letzten Teilaufgabe sollen Sie entscheiden, welches Diagramm zum $\text{ Coder A }$ gehört und welches zum $\text{ Coder B}$.
Zunächst werden die drei Übertragungsfunktionen
- $G(D) = 1 + D + D^2 + D^3$,
- $G(D) = 1 + D^3$, und
- $G(D) = 1 + D + D^3$
analysiert und anschließend die Ausgangssequenzen $\underline{x}$ unter der Voraussetzung
- $$\underline{u}= \underline{1}= (1, 1, 1, \text{...} \hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} U(D)= \frac{1}{1+D}$$
berechnet. Diese Übertragungsfunktionen stehen im direkten Zusammenhang mit den skizzierten Codierern.
- Desweiteren ist noch zu klären, welcher der beiden Codes „katastrophal” ist.
- Von einem solchen spricht man dann, wenn eine endliche Anzahl von Übertragungsfehlern zu unendlich vielen Decodierfehlern führt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.
- Bezug genommen wird insbesondere auf die Abschnitte
- Angegeben werden noch zwei Polynomprodukte in ${\rm GF}(2)$:
- $$(1+D) \cdot (1+D^2) = 1+D +D^2+D^3\hspace{0.05cm},$$
- $$(1+D) \cdot (1+D+D^2) = 1+D^3\hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1) Zutreffend sind die Lösungsvorschläge 2 und 4:
- Die $D$–Transformierte der Codesequenz $\underline{x}$ ergibt sich mit $U(D) = 1/(1+ D)$ zu
- $$X(D)= \frac{1+D +D^2+D^3}{1+D}= 1 +D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}.$$
- Berücksichtigt wurde $(1 + D) \cdot (1 + D^2) = 1 + D + D^2 + D^3$.
(2) Wegen $(1 + D) \cdot (1 + D + D^2) = 1 + D^3$ sind hier die Lösungsvorschläge 3 und 4 zutreffend:
- $$X(D)= \frac{1+D^3}{1+D}= 1 +D + D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.05cm}.$$
(3) Richtig ist allein der Lösungsvorschlag 1:
- Die Polynomdivision $(1 + D + D^3)$ durch $(1 + D)$ ist im binären Galoisfeld nicht ohne Rest möglich.
- Man erhält $X(D) = 1 + D^3 + D^4 + D^5 + \ \text{...} \hspace{0.05cm} $ ⇒ Ausgangssequenz $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$, die sich bis ins Unendliche erstreckt.
(4) Richtig ist allein der Lösungsvorschlag 1:
- Die Übertragungsfunktionsmatrix von $\text{ Coder A }$ lautet:
- $${\boldsymbol{\rm G}}_{\rm A}(D)= \left (1 +D + D^3\hspace{0.05cm}, \hspace{0.15cm} 1+D +D^2+D^3 \right ) \hspace{0.05cm}.$$
- Das jeweils erste Codebit ist deshalb durch die Sequenz entsprechend Teilaufgabe (3) gegeben und das zweite Bit durch die Sequenz entsprechend Teilaufgabe (1):
- $$\underline{x}^{(1)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}, \hspace{1cm} \underline{x}^{(2)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.01cm})\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x}= (11,\hspace{0.05cm} 00,\hspace{0.05cm} 01,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.01cm})\hspace{0.05cm}.$$
(5) Zutreffend sind die Lösungsvorschläge 2 und 4:
- Die Übertragungsfunktion von $\text{ Coder B }$ lautet $\mathbf{G}_{\rm B} = (1 + D^3, \ 1 + D + D^2 + D^3)$.
- Die erste Codesequenz ergibt sich nun entsprechend Teilaufgabe (2), während $\underline{x}^{(2)}$ weiterhin der Teilaufgabe (1) entspricht.
- Somit erhält man hier $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$ ⇒ Lösungsvorschlag 2.
- Richtig ist aber auch der Lösungsvorschlag 4. Unter der hier getroffenen Annahme $\underline{u} = \underline{1}$ beinhaltet die Codesequenz $\underline{x}$ nur fünf Einsen.
- In der nächsten Teilaufgabe wird dieser Sachverhalt nochmals aufgegriffen.
(6) Richtig sind die Lösungsvorschläge 2 und 3:
Wie aus dem Zustandsdiagramm 1 hervorgeht, führt hier die Informationssequenz $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$ zur Codesequenz $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$. Dies bedeutet:
- Zum $\text{ Coder A }$ gehört das Zustandsübergangsdiagramm 1.
- Zum $\text{ Coder B }$ gehört das Zustandsübergangsdiagramm 2 ⇒ Lösungsvorschlag 2.
Für den $\text{ Coder B }$ gelten dabei folgende Aussagen:
- $\underline{u} = \underline{0} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm}) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (00, \, 00, \, 00, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$,
- $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm}) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$.
Das bedeutet:
- Mit nur fünf Bitfehlern an den Positionen 1, 2, 3, 5, 6 wird die Nullfolge als Einsfolge decodiert und umgekehrt.
- Einen solchen Code nennt man katastrophal ⇒ Lösungsvorschlag 3.
