Exercise 3.10Z: Amplitude and Angle Modulation in Comparison

• Return to book

Kennlinien zur Beschreibung des Rauschverhaltens bei  $\rm AM$  und  $\rm WM$

Betrachtet wird die Übertragung eines Cosinussignals mit Amplitudenmodulation  $\rm (AM)$  und Winkelmodulation  $\rm (WM)$.  Es gelten folgende Randbedingungen:

• Nachrichtenfrequenz  $f_{\rm N} = 10 \ \rm kHz$,
• Sendeleistung  $P_{\rm S} = 100 \ \rm kW$,
• Kanalübertragungsfaktor  $20 · \lg α_{\rm K} = -120 \ \rm dB$,
• Rauschleistungsdichte  $N_0 = 10^{–16} \ \rm W/Hz$.

Diese Systemparameter werden zweckmäßigerweise zur gemeinsamen Leistungskenngröße

$$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$

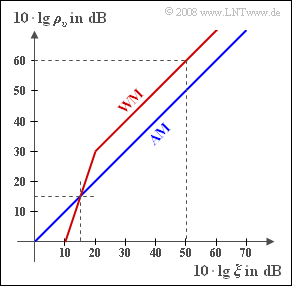
zusammengefasst.  Die Grafik zeigt den sich ergebenden Sinken–Störabstand  $10 · \lg ρ_v$  in Abhängigkeit der logarithmierten Leistungskenngröße  $ξ$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Rauscheinfluss bei Winkelmodulation.
• Bezug genommen wird aber auch auf den Abschnitt  Sinken-SNR und Leistungskenngröße  sowie auf das Kapitel  Frequenzmodulation.

• Es gelten folgende Beziehungen:

$$\rho_{v } = \left\{ \begin{array}{c} \xi \\ {\eta^2}/2 \cdot\xi \\ 3{\eta^2}/2 \cdot\xi \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}l} {\rm ZSB/ESB-AM \hspace{0.15cm}ohne \hspace{0.15cm}Tr\ddot{a}ger} \hspace{0.05cm}, \\ {\rm PM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta } \hspace{0.05cm}, \\ {\rm FM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta }\hspace{0.05cm}. \\ \end{array}$$

• Die Bandbreiten  $B_{\rm K}$  bei Winkelmodulation sind gemäß der  „Carson–Regel”  so zu wählen, dass ein Klirrfaktor  $K < 1\%$  garantiert werden kann:

$$ B_{\rm K} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie die logarithmierte Leistungskenngröße  $ξ$.

$10 · \lg \ ξ \ = \ $ $\ \rm dB$

2

Welcher Sinkenstörabstand ergibt sich beim AM–System?

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

3

Welche spezielle Form der AM könnte hier vorliegen?

	Es könnte eine ZSB–AM sein.
	Es könnte eine ESB–AM sein.
	Es könnte eine AM ohne Träger sein.
	Es könnte eine AM mit zugesetztem Träger sein.

4

Wie groß ist im Fall der ZSB–AM die erforderliche Kanalbandbreite  $B_{\rm K}$?

$B_{\rm K} \ = \ $ $\ \rm kHz$

5

Wie groß ist der Sinkenstörabstand beim WM-System?

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

6

Welche Bandbreite ist beim vorgegebenen PM–System mindestens erforderlich, wenn  $K < 1\%$  gelten soll?

$B_{\rm K} \ = \ $ $\ \rm kHz$

7

Wie groß ist für  $K < 1\%$  die erforderliche Bandbreite, wenn das WM–System eine Frequenzmodulation realisiert?

$B_{\rm K} \ = \ $ $\ \rm kHz$

8

Wie groß muss bei sonst gleichen Parametern die Sendeleistung  $P_{\rm S}$  mindestens sein, damit das WM–System nicht schlechter als das AM–System ist?

$P_{\rm S,\hspace{0.05cm}min} \ = \ $ $\ \rm W$

Musterlösung

Solution

(1)  Aus  $20 · \lg α_{\rm K} = -120 \ \rm dB$  erhält man  $α_{\rm K} = 10^{–6}$.  Damit ergibt sich mit  $B_{\rm NF} = f_{\rm N}$:

$$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}= \frac{10^{-12} \cdot 10^{5}\;{\rm W}}{10^{-16}\;{\rm W/Hz} \cdot 10^{4}\;{\rm Hz}}= 10^5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$

(2)  Aus der Grafik ist zu entnehmen, dass beim AM–System  $ρ_v = ξ$  gilt.  Damit ergibt sich für den Sinken-Störabstand:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$

(3)  Richtig sind die ersten drei Lösungsvorschläge:

• Es handelt sich um eine ZSB–AM oder eine ESB–AM, jeweils ohne Träger.
• Dagegen scheiden die ZSB–AM und die ESB–AM mit Träger aus.  In diesen Fällen würde stets  $ρ_v < \xi$  sein.

(4)  Bei der ZSB–AM muss  $B_{\rm K} ≥ 2 · f_{\rm N}\hspace{0.15cm}\underline { = 20 \ \rm kHz}$  gelten.

(5)  Aus der angegebenen Grafik erkennt man, dass ab etwa  $20 \ \rm dB$  gilt:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 10 \cdot {\rm lg} \hspace{0.15cm}\xi + 10\,{\rm dB}. \hspace{0.3cm}{\rm Mit}\hspace{0.15cm}10 \cdot {\rm lg} \hspace{0.15cm}\xi = 50\,{\rm dB}\hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 60\,{\rm dB}}.$$

(6)  Bei Phasenmodulation gilt:

$$ \rho_{v }= \frac{\eta^2}{2} \cdot \xi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta^2 = \frac{2 \cdot \rho_{v }}{\xi} = 20\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 4.47 \hspace{0.05cm}.$$

• Damit muss für die Kanalbandbreite unter der Voraussetzung  $K < 1\%$  gelten:

$$B_{\rm K} \ge 2 \cdot f_{\rm N} \cdot (\eta +2) = 20\,{\rm kHz}\cdot 6.47 \hspace{0.15cm}\underline { \approx 130\,{\rm kHz}}\hspace{0.05cm}.$$

(7)  Hier genügt ein kleinerer Modulationsindex und damit auch eine kleinere Bandbreite:

$${3}/{2}\cdot \eta^2 = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 2.58 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}B_{\rm K} = 20\,{\rm kHz}\cdot 4.58 \hspace{0.15cm}\underline {\approx 91.6\,{\rm kHz}}\hspace{0.05cm}.$$

(8)  In der Grafik erkennt man den so genannten FM–Knick.

• Für  $10 · \lg \hspace{0.08cm} ξ = 15 \ \rm dB$  erhält man für das WM–System genau das gleiche Sinken–SNR wie für das AM–System.
• Die Sendeleistung kann also um  $35 \ \rm dB$  kleiner sein als  $100 \ \rm kW$:

$$ 10 \cdot {\rm lg} \hspace{0.15cm}\frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}= -35\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}\approx 0.0003\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm S,\hspace{0.05cm}min} \hspace{0.15cm}\underline {\approx 30\,{\rm W}}\hspace{0.05cm}.$$