System Description in Frequency Domain

1 # OVERVIEW OF THE FIRST MAIN CHAPTER #
2 The Cause-Effect Principle
3 Application in Communications Engineering
4 Prerequisites for the Application of Systems Theory
5 Transfer function – Frequency response
6 Properties of the Frequency Response
7 Lowpass, Highpass, Bandpass and Bandstop
8 Test Signals for Measuring the Frequency Response
9 Exercises for the Chapter

# OVERVIEW OF THE FIRST MAIN CHAPTER #

In the book "Signal Representation" you were familiarised with the mathematical description of deterministic signals in the time and frequency domain. The second book "Linear Time-Invariant Systems" now describes which changes a signal or its spectrum undergoes through an information system and how these changes can be captured mathematically.

$\text{Please note:}$

The "system" can be a simple circuit as well as a complete, highly complicated transmission system with a multitude of components.
It is only assumed here that the system has the two properties ”linear” and ”time-invariant”.

In the first chapter, the basics of the so-called systems theory are mentioned, which allows a uniform and simple description of such systems. We start with the system description in the frequency domain with the partial aspects listed above.

Further information on the topic as well as tasks, simulations and programming exercises can be found in

Chapter 6: Linear Time-Invariant Systems (Programme lzi)

of the practical course "Simulation Methods in Communications Engineering". This (former) LNT course at the TU Munich is based on

the educational software package LNTsim ⇒ Link refers to the ZIP version of the programme, and
this practical course guide Praktikumsanleitung ⇒ Link refers to the PDF-version; Chapter 6: pages 99-118.

The Cause-Effect Principle

Einfachstes Systemmodell

In this chapter we always consider the simple model outlined on the right.

This arrangement is to be interpreted as follows:

The focus is on the so-called system, which is largely abstracted in its function ("black box"). Nothing is known in detail about the realisation of the system.
The time-dependent input variable $x(t)$ acting on this system is also referred to as the cause function in the following.
At the output of the system, the effect function $y(t)$ then appears - quasi as a response of the system to the input function $x(t)$.

Note: the system can generally be of any kind and is not limited to communications technology alone. Rather, attempts are also made in other fields of science, such as the natural sciences, economics and business administration, sociology and political science, to capture and describe causal relationships between different variables by means of the cause-effect principle.

However, the methods used for these phenomenological system theories differ significantly from the approach in communications engineering, which is outlined in this first main chapter of the present book "Linear Time-Invariant Systems".

Application in Communications Engineering

The cause-effect principle can also be applied in communications engineering, for example to describe two-poles. Here one can consider the current curve $i(t)$ as a cause function and the voltage $u(t)$ as an effect function. By observing the I/U relationships, conclusions can be drawn about the properties of the actually unknown two-pole.

Karl Küpfmüller introduced the term "systems theory" for the first time (in Germany) in 1949. He considers it as a method for describing complex causal relationships in natural sciences and technology, based on a spectral transformation - for example, the Fouriertransformation presented in the book "Signal Representation".

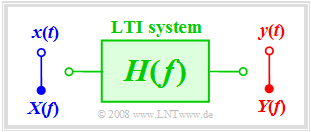
Allgemeines Modell der Nachrichtenübertragung

An information system can entirely be described in therms of systems theory. Here

the cause function is the input signal $x(t)$ or its spectrum $X(f)$,
the response function is the output signal $y(t)$ or its spectrum $Y(f)$.

Also in the following pictures, the input variables are mostly drawn in blue, the output variables in red and system variables in green.

$\text{Example 1:}$ If the "information system" describes a given linear circuit, then given a known input signal $x(t)$ the output signal $y(t)$ can be predicted with the help of systems theory. A second task of systems theory is to classify the information system by measuring $y(t)$ knowing $x(t)$ but without knowing the system in detail.

If $x(t)$ describes, for instance, the voice of a caller in Hamburg and $y(t)$ the recording of an answering machine in Munich, then the "information system" consists of the following components:

microphone – telephone – electrical line – signal converter – fibre optic cable – optical amplifier – signal resetter – receive filter (for example for equalisation and noise limitation) – ... – electromagnetic transducer.

Prerequisites for the Application of Systems Theory

The model of a messaging or information system given above holds generally and independently of the boundary conditions. However, the application of systems theory requires some additional limiting preconditions.

Unless explicitly stated otherwise, the following shall always apply:

Both $x(t)$ and $y(t)$ are deterministic signals. Otherwise, one must proceed according to the page Stochastische Systemtheorie in the book "Theory of Stochastic Signals".
The system is linear. This can be seen, for example, from the fact that a harmonic oscillation $x(t)$ at the input also results in a harmonic oscillation $y(t)$ of the same frequency at the output:

$$x(t) = A_x \cdot \cos(\omega_0 \hspace{0.05cm}t - \varphi_x)\hspace{0.2cm}\Rightarrow \hspace{0.2cm} y(t) = A_y \cdot\cos(\omega_0 \hspace{0.05cm}t - \varphi_y).$$

New frequencies do not arise. Only amplitude and phase of the harmonic oscillation can be changed. Non-linear systems are treated in the chapter Nichtlineare Verzerrungen .
Because of linearity, the superposition principle is also applicable. This states that due to $x_1(t) ⇒ y_1(t)$ and $x_2(t) ⇒ y_2(t)$ the following mapping also necessarily holds:

$$x_1(t) + x_2(t) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y_1(t) + y_2(t).$$

The system is time-invariant. This means that an input signal shifted by $\tau$ results in the same output signal – but this is also delayed by $\tau$ :

$$x(t - \tau) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y(t -\tau)\hspace{0.4cm}{\rm falls} \hspace{0.4cm}x(t )\hspace{0.2cm}\Rightarrow \hspace{0.1cm} y(t).$$

Time-varying systems are discussed in the book Mobile Kommunikation .

If all the conditions listed here are fulfilled, one deals with a linear time-invariant system, abbreviated LTI–system. In the German-language literature the abbreviation LZI (linear zeitinvariant) is commonly used.

Transfer function – Frequency response

We assume an LTI-system whose input and output spectra $X(f)$ and $Y(f)$ are known or can be derived from the time signals $x(t)$ and $y(t)$ via Fouriertransformation .

Definition of the Frequency Response

$\text{Definition:}$ The transmission behaviour of a messaging system is described in the frequency domain by the transfer function :

$$H(f) = \frac{Y(f)}{X(f)}= \frac{ {\rm response\:function} }{ {\rm cause\:function} }.$$

Other terms for $H(f)$ are "system function" and "frequency response". In the following we will mainly use the latter.

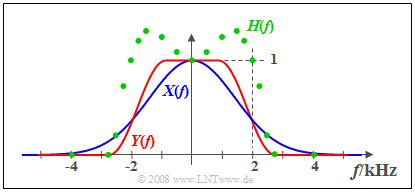
Input Spectrum, Output Spectrum and Frequency Response

$\text{Example 2:}$ The signal $x(t)$ with the real spectrum $X(f)$ (blue curve) is applied to the input of an LTI-system. The measured output spectrum $Y(f)$ – marked red in the graph – is larger than $X(f)$ at frequencies lower than $2 \ \rm kHz$ and has a steeper slope in the region around $2 \ \rm kHz$ . Above $2.8 \ \rm kHz$ the signal $y(t)$ has no spectral components.

The green circles mark some measuring points of the frequency response

$$H(f) = Y(f)/X(f)$$ which is real, too.

At low frequencies $H(f)>1$: In this range the LTI-system has an amplifying effect.
The frequency roll-off of $H(f)$ is similar to that of $Y(f)$ but not identical.

Properties of the Frequency Response

The frequency response $H(f)$ is a central variable in the description of communication systems.

Some properties of this important system variable are listed below:

The frequency response describes the LTI–system on its own. It can be calculated, for example, from the linear components of an electrical network. With a different input signal $x(t)$ and a correspondingly different output signal $y(t)$ the result is exactly the same frequency response $H(f)$.
$H(f)$ can have a ”unit”. For example, if one considers the voltage curve $u(t)$ as a cause and the current $i(t)$ as effect for a two-pole, the frequency response $H(f) = I(f)/U(f)$ has the unit $\rm A/V$. $I(f)$ and $U(f)$ are the Fourier transforms of $i(t)$ and $u(t)$, respectively.
In the following we consider only quadripoles. Moreover, without loss of generality, we usually assume that $x(t)$ and $y(t)$ are voltages, respectively. In this case $H(f)$ is always dimensionsless.
Since the spectra $X(f)$ and $Y(f)$ are generally complex, the frequency response $H(f)$ is also a complex function. The magnitude $|H(f)|$ is called the amplitude response. This is also often represented in logarithmic form and called the damping curve :

$$a(f) = - \ln |H(f)| = - 20 \cdot \lg |H(f)|.$$

Depending on whether the first form with the natural logarithm or the second with the decadic logarithm is used, the pseudo-unit ”neper” (Np) or ”decibel” (dB) must be added.
The phase response can be calculated from $H(f)$ in the following way:

$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$

Thus, the total frequency response can also be represented as follows:

$$H(f) = \vert H(f)\vert \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm} \cdot\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{ - {\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$

Lowpass, Highpass, Bandpass and Bandstop

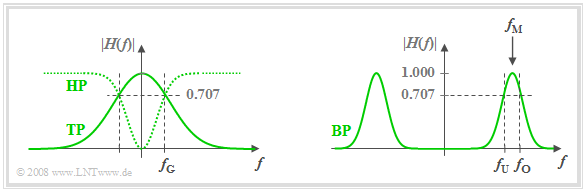
According to the amplitude response $|H(f)|$ one distinguishes between

lowpass: Signal components tend to be more attenuated with increasing frequency.
highpass: HHere, high-frequency signal components are attenuated less than low-frequency ones. A direct signal $($that is, a signal component with the frequency $f = 0)$ cannot be transmitted via a highpass.
bandpass: There is a preferred frequency called the centre frequency $f_{\rm M}$ . The further away the frequency of a signal component is from $f_{\rm M}$ , the more it will be attenuated.
bandstop: This is the counterpart to the bandpass and it is $|H(f_{\rm M})| ≈ 0$. However, very low-frequency and very high-frequency signal components are let pass.

Lowpass and Highpass (left), and Bandpass (right)

The graph shows the amplitude responses of the filter types ”lowpass” (LP) and ”highpass” (HP) (left), and ”bandpass” (BP) (right).

Also shown are the cutoff frequencies $f_{\rm G}$ (for lowpass and highpass) or $f_{\rm U}$ and $f_{\rm O}$ (for bandpass).
These denote 3dB-cutoff frequencies here, for example, according to the following definition.

$\text{Definition:}$ The 3dB–cutoff frequency of a lowpass filter specifies the frequency $f_{\rm G}$ , for which holds:

$$\vert H(f = f_{\rm G})\vert = {1}/{\sqrt{2} } \cdot \vert H(f = 0)\vert \hspace{0.5cm}\Rightarrow\hspace{0.5cm} \vert H(f = f_{\rm G})\vert^2 = {1}/{2} \cdot \vert H(f = 0) \vert^2.$$

Note that there are also a number of other definitions for the cut-off frequency.
These can be found on the page Allgemeine Bemerkungen in the chapter ”Einige systemtheoretische Tiefpassfunktionen” .

Test Signals for Measuring the Frequency Response

For measuring the frequency response $H(f)$ any input signal $x(t)$ with spectrum $X(f)$ is suitable, as long as $X(f)$ has no zeros (in the range of interest). By measuring the output spectrum $Y(f)$ the frequency response can thus be determined in a simple way:

$$H(f) = \frac{Y(f)}{X(f)}.$$

In particular, the following input signals are suitable:

Dirac delta function $x(t) = K · δ(t)$ ⇒ spectrum $X(f) = K$:

Thus, the frequency response by magnitude and phase is of the same shape as the output spectrum $Y(f)$ and it holds $H(f) = 1/K · Y(f)$. If one approximates the Dirac delta function by a narrow rectangle of equal area $K$, then $H(f)$ must be corrected by means of a ${\rm sin}(x)/x$–function.

Dirac puls – the infinite sum of equally weighted Dirac delta functions at the time interval $T_{\rm A}$:

This leads according to the chapter Zeitdiskrete Signaldarstellung in the book ”Signal Representation” to a Dirac pulse in the frequency domain with distance $f_{\rm A} =1/T_{\rm A}$. This allows a discrete frequency measurement of $H(f)$ with the spectral samples spaced $f_{\rm A}$.

Harmonische oscillation $x(t) = A_x · \cos (2πf_0t - φ_x)$ ⇒ dirac-shaped spectrum at $\pm f_0$:

The output signal $y(t) = A_y · \cos(2πf_0t - φ_y)$ is an oscillation of the same frequency $f_0$. The frequency response for $f_0 \gt 0$ is:

$$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$

To determine the total frequency response $H(f)$ an infinite number of measurements at different frequencies $f_0$ are required.