Exercise 3.8Z: Convolution of Two Rectangles

The convolution of two rectangles $x(t)$ and $h(t)$

At the input of a causal LTI system (i.e. linear and time-invariant)

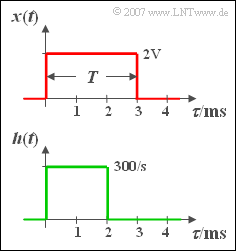
with a rectangular impulse response ${h(t)}$ of duration $2 \,\text{ms}$ ,
a rectangular pulse ${x(t)}$ of duration $T = 3 \,\text{ms}$ and amplitude $A = 2\,\text{ V}$ is applied.

The rectangular functions each start at the time $t = 0$.

In this task you are to calculate the output signal ${y(t)}$ with the help of the "Graphical Convolution".

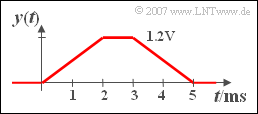
As you can easily check, the output signal ${y(t)}$

differs from zero only in the range between $0$ and $5 \, \text{ms}$, and
is symmetrical at the time $t = 2.5 \, \text{ms}$.

Hints:

This exercise belongs to the chapter "The Convolution Theorem and Operation".
It mainly refers to the page "Graphical Convolution".
The topic of this section is also illustrated in the interactive applet "Graphical Convolution".

Questions

$y(t = 1 \,\text{ms})\ = \ $

$\text{V}$

$y(t = 2 \,\text{ms})\ = \ $

$\text{V}$

$y(t = 3 \,\text{ms})\ = \ $

$\text{V}$

$y(t = 4 \,\text{ms})\ = \ $

$\text{V}$

	The output signal ${y(t)}$ has a trapezoidal shape.
	The spectrum is ${Y(f)} = Y_0 \cdot \text{si}^{2}(\pi f T)$.
	With $T = 2 \,\text{ms}$ , a triangular shape would result.

Solution

To illustrate the graphical convolution $x(t) \star h(t)$

(1) In general, the following applies to the convolution integral:

$$y(t) = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot h( {t - \tau } )}\hspace{0.1cm} {\rm d}\tau.$$

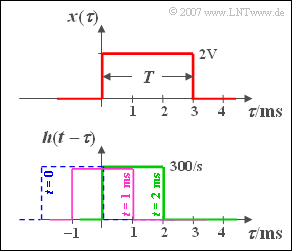
Hints: The abscissas in the graph opposite have been renamed $\tau$ .

The signal value at time $t = 1 \,\text{ms}$ ms can be calculated as follows:

Reflection of the impulse response ${h(\tau)}$,
shift by $t = 1 \text{ ms}$ to the right (violet curve in the sketch),
multiplication of the two functions and integration.

The product is also rectangular with the height $2 \text{ V} \cdot 300 \; \text{1/s}$ and width $1 \,\text{ms}$. This results in for the area:

$$y( {t = 1\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= 0.6\;{\rm{V}}}{\rm{.}}$$

The green rectangle illustrates the calculation of the second signal value. Now the resulting rectangle is twice as wide after the multiplication and we get:

$$y( {t = 2\;{\rm{ms}}} ) = 2\;{\rm{V}} \cdot {\rm{300}}\;{1}/{{\rm{s}}} \cdot 2\;{\rm{ms}}\hspace{0.15 cm}\underline{={\rm{1.2}}\;{\rm{V}}}{\rm{.}}$$

(2) Because of the symmetry of ${y(t)}$ with respect to the time $t = 2.5\, \text {ms}$ holds:

$$y( {t = 3\;{\rm{ms}}} ) = y( {t = 2\;{\rm{ms}}} ) \hspace{0.15 cm}\underline{= {\rm{1}}{\rm{.2}}\;{\rm{V}}}{\rm{,}}$$

$$y( {t = 4\;{\rm{ms}}} ) = y( {t = 1\;{\rm{ms}}} )\hspace{0.15 cm}\underline{ = 0.6\;{\rm{V}}}{\rm{.}}$$

Convolution result $y(t)$

(3) In subtasks (1) and (2) the signal values were calculated at discrete time points.

All points are to be connected by straight line segments, since the integration over rectangular functions of increasing width results in a linear course.
This means: The output signal ${y(t)}$ is trapezoidal.

The associated spectrum is complex and reads:

$$Y(f) = 6 \cdot 10^{ - 3} \;{{\rm{V}}}/{{{\rm{Hz}}}} \cdot {\mathop{\rm si}\nolimits} ( {2\;{\rm{ms}}\cdot{\rm{\pi }}f} ) \cdot {\mathop{\rm si}\nolimits} ( {3\;{\rm{ms}}\cdot{\rm{\pi }}f}) \cdot {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \hspace{0.05cm}\cdot \hspace{0.05cm}2.5\;{\rm{ms}}\hspace{0.05cm}\cdot \hspace{0.05cm} \pi }}f} .$$

If the input pulse ${x(t)}$ had the duration $T = 2\, \text {ms}$, had the duration ${y(t)}$ would show a triangular waveform between ${t = 0}$ and $t = 4 \text { ms}$ .
The maximum $1.2 \, \text {V}$ would then only result at the time $t = 2 \, \text {ms}$.

Proposed solutions 1 and 3 are therefore correct.