Exercise 1.5: Binary Markov Source

Binary Markov diagram

Task 1.4 has shown that the calculation of the entropy for a memory-containing source can be very time-consuming. One must then first calculate (very many) entropy approximations $H_k$ for $k$–tuples and only then can the source entropy be determined with the boundary transition $k \to \infty$ :

$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$

Often, $H_k$ tends only very slowly towards the limit $H$.

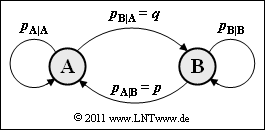
The calculation process is drastically reduced if the message source has Markov properties. The diagram shows the transition diagram for a binary Markov source with the two states (symbols) $\rm A$ and $\rm B$. This is determined by the two conditional Markov sources.

This is clearly determined by the two conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ .
The other conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ as well as the (unconditional) symbol probabilities $p_{\rm A}$ and $p_{\rm B}$ can be determined from this.

The entropy of the binary Markov chain (with the unit „bit/symbol”) is then:

$$H = H_{\rm M} = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

In this equation, it should be noted that in the argument of the binary logarithm , the conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... are to be used, while the joint probabilities $p_{\rm AA}$, $p_{\rm AB}$, ... are to be used for the weighting.

Using the first order entropy approximation,

$$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol})\hspace{0.05cm},$$

as well as the (actual) entropy $H = H_{\rm M}$ given above, all further entropy approximations $(k = 2,, 3, \text{...})$ can also be given directly for a Markov source:

$$H_k = \frac{1}{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M} \big ] \hspace{0.05cm}.$$

Hints:

The task belongs to the chapter Sources with Memory.
Reference is also made in particular to the two pages Schnittmenge und Bedingte Wahrscheinlichkeit.
With the exception of subtask (6) $p = 1/4$ and $q = 1/2$ always apply.

For the (ergodic) symbol probabilities of a first order Markov chain applies:

$$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$

Questions

$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \ = \ $

$p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \ = \ $

$p_{\rm A} \ = \ $

$p_{\rm B} \ = \ $

$H_1 \ = \ $

$\ \rm bit/symbol$

$H \ = \ $

$\ \rm bit/symbol$

$H_2 \ = \ $

$\ \rm bit/symbol$

$H_3 \ = \ $

$\ \rm bit/symbol$

$H_4 \ = \ $

$\ \rm bit/symbol$

$H \ = \ $

$\ \rm bit/symbol$

Solution

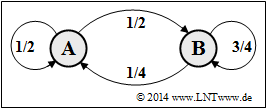
Markovdiagramm für die Teilaufgaben (1), ... , (5)

Nach $\rm A$ sind $\rm A$ und $\rm B$ gleichwahrscheinlich. Nach $\rm B$ tritt $\rm B$ sehr viel häufiger als $\rm A$ auf. Für die Übergangswahrscheinlichkeiten gilt:

$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},$$

$$ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$

(2) Entsprechend den angegebenen Gleichungen gilt:

$$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{0.5cm} p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$

(3) Mit den in der letzten Teilaufgabe berechneten Wahrscheinlichkeiten gilt:

$$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(4) Die Entropie der Markovquelle lautet entsprechend der Angabe:

$$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

Für die Verbundwahrscheinlichkeiten gilt:

$$p_{\rm AA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$

$$ p_{\rm AB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = q \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$

$$ p_{\rm BA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = p \cdot \frac{q}{p+q} = p_{\rm AB} = {1}/{6} \hspace{0.05cm},$$

$$ p_{\rm BB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-p) \cdot \frac{q}{p+q} = \frac{3/4 \cdot 1/2}{3/4} = {1}/{2} $$

$$\Rightarrow\hspace{0.3cm} H = 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = 10/6 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(5) Allgemein gilt mit $H_{\rm M} = H$ für die $k$–te Entropienäherung:

$$H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$$

Daraus folgt:

$$H_2 = {1}/{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/Symbol}} \hspace{0.05cm},$$

$$ H_3 = {1}/{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/Symbol}} \hspace{0.05cm},$$

$$ H_4 = {1}/{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

Markovdiagramm zur Teilaufgabe (6)

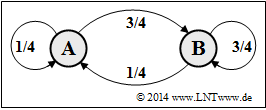
(6) Mit dem neuen Parametersatz $(p = 1/4, q = 3/4)$ erhält man für die Symbolwahrscheinlichkeiten:

$$ p_{\rm A} = 1/4, \ p_{\rm B} = 3/4.$$

Dieser Sonderfall führt demnach zu statistisch unabhängigen Symbolen:

$$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}.$$

Damit ist die Entropie $H$ identisch mit der Entropienäherung $H_1$:

$$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = 2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

Die Entropienäherungen $H_2$, $H_3$, $H_4$, ... liefern hier ebenfalls das Ergebnis $0.811 \, \rm bit/Symbol$.