Exercise 2.7: Huffman Application for Binary Two-Tuples
The application of the Huffman algorithm in its original form assumes a symbol set $M > 2$ and is therefore useless for data compression of binary sources.
However, if one combines several consecutive binary characters of the message source into a new symbol, one can usefully apply Huffman data compression to the new symbol set.
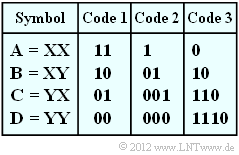
In this task we start from the symbol set $\{$ $\rm X$, $\rm Y$ $\}$ ⇒ aus $(M = 2)$ and form two-tuples according to the table above with the symbol set $\{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$ $\}$ ⇒ $(M\hspace{0.03cm}' = M^2 = 4)$.
For example, the binary source symbol sequence $\rm XYXXYXXXYY$ thus becomes the quaternary sequence $\rm BACAD$.
Furthermore, three codes are given in the above table, some of which have been created by the Huffman algorithm. The binary output sequences then result for our example as follows:
- $\text{Code 1}$: 1011011100,
- $\text{Code 2}$: 0110011000,
- $\text{Code 3}$: 10011001110.
Again for understanding:
- From the original symbol set $\{$ $\rm X$, $\rm Y$ $\}$ a quaternary set with symbol set $\{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$ $\}$ is obtained by forming two-tuples.
- The sequence length $N$ is thereby halved to $N\hspace{0.03cm}' = N/2 $ .
- Huffman coding again results in a binary sequence whose symbol set is designated $\{$0, 1$\}$ for better differentiation.
- The application of Huffman coding makes sense exactly when the length $L$ of the initial sequence is smaller than $N$ (on statistical average).
This task is intended to clarify which of the given binary codes make sense under which boundary conditions.
- Let the binary message source $\{$ $\rm X$, $\rm Y$ $\}$ be memoryless and be described solely by the symbol probability $p_{\rm X}$ .
- The second probability is then always $p_{\rm Y} = 1 - p_{\rm X}$.
Hints:
- The task belongs to the chapter Entropy Coding according to Huffman.
- In particular, reference is made to the page Application of Huffman coding to $k$-tuples Bezug genommen.
- The mean codeword length per two-tuple is $L_{\rm M}\hspace{0.03cm}' = p_{\rm A} \cdot L_{\rm A} +$ ... $ + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}$. With respect to a source symbol, $L_{\rm M} = L_{\rm M}\hspace{0.03cm}'/2$.
- A comparable task with ternary input symbols is treated in exercise 2.7Z .
- The idea for this task arose during a lecture by Prof. Robert Fischer from the University of Ulm at the Technical University of Munich on the topic of "Der goldene Schnitt in der Nachrichtentechnik".
Questions
Solution
- $$L_{\rm M} = \big [ \hspace{0.05cm}p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B} + p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm} \big ] / 2 = \big [ \hspace{0.05cm} L_{\rm A} + L_{\rm B} + L_{\rm C} + L_{\rm D}\hspace{0.05cm} \big ] / 8 \hspace{0.05cm}.$$
Berücksichtigt man die angegebenen Zuordnungen, so erhält man für
- $\text{Code 1}$: $L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/Quellensymbol} }$,
- $\text{Code 2}$: $L_{\rm M} \hspace{0.15cm}\underline{= 1.125 \ {\rm bit/Quellensymbol} }$,
- $\text{Code 3}$: $L_{\rm M} \hspace{0.15cm}\underline{= 1.250 \ {\rm bit/Quellensymbol} }$.
- Im Verlauf der Aufgabe wird sich zeigen, dass die beiden ersten Codes durchaus als Ergebnis des Huffman–Algorithmus möglich sind (natürlich nur bei geeigneten Symbolwahrscheinlichkeiten). Der $\text{Code 3}$ ist zwar ebenfalls präfixfrei, aber hinsichtlich der mittleren Codewortlänge nie optimal.
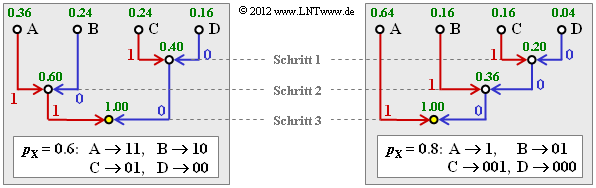
(2) Die Wahrscheinlichkeiten der möglichen Zweiertupel lauten:
- $$p_{\rm A} = 0.6^2 = 0.36 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.6 \cdot 0.4 = 0.24 = p_{\rm C} \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.4^2 = 0.16 \hspace{0.05cm}.$$
- Damit ergibt sich das linke Baumdiagramm (in nebenstehender Grafik) und der folgende Huffman–Code:
- $\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 00.
- Es handelt sich um den $\text{Code 1}$ ⇒ Lösungsvorschlag 1.
(3) Jedes Zweiertupel wird durch zwei Bit dargestellt. Damit ist
- $$L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/Quellensymbol} }.$$
(4) Hier lauten die Wahrscheinlichkeiten der einzelnen Zweiertupel:
- $$p_{\rm A} = 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 \hspace{0.05cm}, $$
- $$p_{\rm C} = p_{\rm B}= 0.8 = 0.16 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.2^2 = 0.04 \hspace{0.05cm}. $$
Entsprechend dem rechten Baumdiagramm ergibt sich nun der $\text{Code 2}$ ⇒ Lösungsvorschlag 2:
- $\rm A$ → 1, $\rm B$ → 01, $\rm C$ → 001, $\rm D$ → 010.
(5) Beim $\text{Code 2}$ gilt für die mittlere Zweiertupellänge bzw. die mittlere Codewortlänge:
- $$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 1 + 0.16 \cdot 2 + (0.16 + 0.04) \cdot 3 = 1.56\,{\rm bit/Zweiertupel}\hspace{0.3cm} \Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.78\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$
(6) Aus den früheren Teilaufgaben hat sich ergeben:
- Für $p_{\rm X} = 0.6$ ist der $\text{Code 1}$ optimal und die mittlere Codewortlänge dieses Codes ist $($unabhängig von $p_{\rm X})$ $L_{\rm M} = 1$ bit/Quellensymbol.
- Für $p_{\rm X} = 0.8$ entsprechend der Teilaufgabe (4) ist der $\text{Code 2}$ optimal und die mittlere Codewortlänge beträgt $L_{\rm M} = 0.78$ bit/Quellensymbol.
Der gesuchte Maximalwert $p_\text{X, max}$ wird somit zwischen $0.6$ und $0.8$ liegen. Die Bestimmungsgleichung ist dabei, dass für den Grenzfall $p_\text{X} = p_\text{X, max}$ beide Codes genau die gleiche mittlere Codewortlänge $L_{\rm M} = 1$ bit/Quellensymbol besitzen, bzw. $L_{\rm M}\hspace{0.03cm}' = 2$ bit/Zweiertupel.
- Mit der Abkürzung $p = p_\text{X, max}$ lautet die entsprechende Bestimmungsgleichung:
- $$L_{\rm M}\hspace{0.01cm}'\hspace{0.15cm}{\rm (Code \hspace{0.15cm}2)} = p^2 \cdot 1 + p \cdot (1-p) \cdot 2 + p \cdot (1-p) \cdot 3 + (1-p)^2 \cdot 3 \stackrel{!}{=} 2 \hspace{0.05cm}.$$
- Dies führt zum zahlenmäßigen Ergebnis:
- $$p^2 + p - 1 \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} p_{\rm X,\hspace{0.05cm}max} = p = \frac{\sqrt{5}-1}{2} \hspace{0.15cm}\underline{ \approx 0.618} \hspace{0.05cm}.$$
- Da sich die grundsätzliche Huffman–Struktur durch Vertauschen von $\rm X$ und $\rm Y$ nicht ändert, gilt für die untere Grenze:
- $$p_{\rm X,\hspace{0.05cm}min} = 1 - p_{\rm X,\hspace{0.05cm}max}\hspace{0.15cm}\underline{ \approx 0.382} \hspace{0.05cm}.$$
Die Darstellung der Zweiertupel durch unterschiedlich lange Bitfolgen $\text{(Code 2)}$ macht also nur Sinn, wenn sich die Symbolwahrscheinlichkeiten von $\rm X$ und $\rm Y$ signifikant unterscheiden. Liegen diese dagegen zwischen $0.382$ und $0.618$, so ist der $\text{Code 1}$ anzuwenden.
- Die Aufteilung einer Strecke der Länge $1$ in zwei Abschnitte der Länge $0.618$... und $0.382$... bezeichnet man als Goldenen Schnitt, auf den man in den verschiedensten Fachgebieten immer wieder stößt.