Exercise 2.10: Shannon-Fano Coding

Tree diagram of the
Shannon-Fano coding

Another algorithm for entropy coding was given in 1949 by Claude Elwood Shannon and Robert Fano , which is described in the theory section.

This special type of source coding will be described here using a simple example for the symbol range $M = 4$ and the following symbol probabilities:

$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$

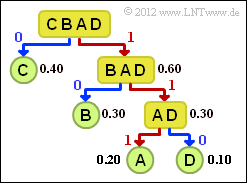
The graph shows the corresponding tree diagram. Proceed as follows:

1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.

2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$.

3. The binary symbol 0is assigned to the less probable group, 1 to the other group.

4. If there is more than one symbol in a group, the algorithm is to be applied recursively.

For this example, the following code assignment results (in the tree diagram, a red connection marks a 1 and a blue one a 0:

$\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.

This gives the following for the mean codeword length:

$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\:symbol}\hspace{0.05cm}.$$

The Huffman algorithm would produce a slightly different code here, but even in this case

$\rm C$ is coded with one bit,
$\rm B$ with two bits and
$\rm A$ and $\rm D$ with three bits each.

This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\:symbol$.

In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities

$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$

determine. You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency.

With the Huffman code, the following assignment results with the probabilities at hand:

$\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.

Hints:

The assignment belongs to the chapter Other source coding methods.
In particular, reference is made to the page The Shannon-Fano algorithm.
To check your results, please refer to the interactive applet Huffman and Shannon-Fano coding.

Questions

$L_{\rm M}\ = \ $

$\ \rm bit/source\:symbol$

	$\rm A$ and $\rm B$ are combined into the first group.
	$\rm B$ and $\rm E$ are combined into the first group.
	The first group consists only of symbol $\rm B$.

	The character $\rm A$ is binary coded with 010 .
	The character $\rm B$ is binary coded with 11 .
	The character $\rm C$ is binary coded with 00110 .

$L_{\rm M}\ = \ $

$\ \rm bit/source\:symbol$

	$L_{\rm M}$ could be smaller for "Shannon–Fano" than for "Huffman".
	$L_{\rm M}$ could be larger at "Shannon–Fano" than at "Huffman".
	$L_{\rm M}$ could be the same for "Shannon–Fano" and "Huffman".

Solution

(1) For the given Huffman code one obtains:

$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$

(2) The correct answer is 2:

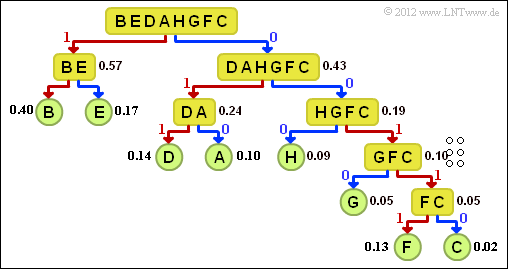
Before applying the Shannon-Fano algorithm, the characters must first be sorted according to their occurrence probabilities. Thus, answer 1 is incorrect.
All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step:

$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$

Tree diagram of Shannon-Fano coding

With the distribution according to solution suggestion 3, the equal distribution would be achieved even less:

$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$

(3) All suggeted solutionss are correct:

The graph shows the tree diagram of the Shannon-Fano coding.
This results in the following assignment (a red connection indicates a 1 , a blue one indicates a 0):

$\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,

${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.

(4) Using the result of sub-task (3) , we get:

$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$

(5) Statements 2 and 3 are correct:

In the present example, Shannon-Fano results in a less favourable value than Huffman.
In most cases – including the example on the information page – Huffman and Shannon-Fano result in an equivalent code and thus also the same average code word length.
Shannon-Fano, on the other hand, never delivers a more effective code than Huffman.