Exercise 2.5Z: Compression Factor vs. Residual Redundancy

Data length $L(N)$ after LZW coding for $\rm BQ1$ and $\rm BQ2$

As in Exercise 2.5 we consider data compression using the Lempel–Ziv–Welch–algorithm. Here holds:

Let the input sequence have length $N$.
The length of the LZW coder output is $L$.

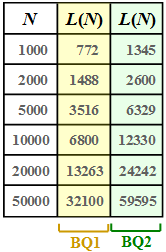
The graph shows for two different binary sources $\rm BQ1$ and $\rm BQ2$ the relationship between the sequence lengths $N$ and $L$, represented by the function $L(N)$.

The two message sources have the same statistical properties as in Exercise 2.5:

$\rm BQ1$ is redundant due to unequal symbol probabilities $(p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11)$ . There are no ties between the individual symbols. The entropy is $H = 0.5$ bit/source symbol.
$\rm BQ2$ is redundancy-free and thus has entropy $H = 1$ bit/source symbol.

Furthermore, you need two definitions for the solution of this task:

Let the compression factor be by definition

$$K(N) = \frac{L(N)}{N}\hspace{0.05cm}.$$

The relative redundancy of the LZW code sequence (called residual redundancy in the following) is

$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$

Hints:

The task belongs to the chapter Compression according to Lempel, Ziv and Welch.
In particular, reference is made to the pages

Residual redundancy as a measure of the efficiency of coding methods,

Efficiency of Lempel-Ziv coding and

Quantitative statements on asymptotic optimality.

Questions

$\rm BQ1$: $K(N = 10000) \ = \ $

$\rm BQ2$: $K(N = 10000) \ = \ $

$\rm BQ1$: $r(N = 10000) \ = \ $

$\ \%$

$\rm BQ2$: $r(N = 10000) \ = \ $

$\ \%$

	For both sources $K(N = 50000)$ is smaller than $K(N = 10000)$.
	For both sources $r(N = 50000)$ is smaller than $r(N = 10000)$.
	Only $\rm BQ1$ has more favourable values with $N = 50000$ .

Solution

(1) The compression factor is defined as the quotient of the lengths of the LZW output sequence $(L)$ and input sequence $(N = 10000)$:

$${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm},$$

$$ {\rm BQ2:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{12330}{10000}\hspace{0.15cm}\underline{= 1.233}\hspace{0.05cm}. $$

Of course, the LZW coding only makes sense with the redundant binary source $\rm BQ1$ . Here the amount of data can be reduced by $32\%$ .
With the redundancy-free binary source $\rm BQ2$ , on the other hand, the LZW coding leads to a $23.3\%$ larger data quantity.

(2) From the given equation we obtain with $N = 10000$:

$${\rm BQ1:}\hspace{0.3cm} H = 0.5\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{0.5 \cdot N}{L } = 1 - \frac{5000}{6800 } \hspace{0.15cm}\underline{\approx 26.5\,\%}\hspace{0.05cm},$$

$$ {\rm BQ2:}\hspace{0.3cm} H = 1.0\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{N}{L } = 1 - \frac{10000}{12330 } \hspace{0.15cm}\underline{\approx 19\,\%}\hspace{0.05cm}.$$

The residual redundancy indicates the (relative) redundancy of the LZW output sequence.
Although the source $\rm BQ1$ is more suitable for LZW coding than the redundancy-free source $\rm BQ2$, $\rm BQ1$ results in a larger residual redundancy because of the redundancy in the input sequence.
A smaller residual redundancy $r(N)$ for a given $N$ therefore says nothing about whether LZW coding is useful for the source at hand.
For this, the compression factor $K(N)$ must be considered. In general, the following relationship between $r(N)$ and $K(N)$ applies:

$$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0.5cm} K(N) = H \cdot (1- r(N)) \hspace{0.05cm}.$$

(3) From the table on the information page one can read (or deduce)

for the redundant binary source $\rm BQ1$:

$$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 0.642\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 22.2\,\% \hspace{0.05cm}},$$

for the redundancy-free binary source $\rm BQ2$:

$$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 1.192\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 16.1\,\% \hspace{0.05cm}}.$$

Statements 1 and 2 are therefore correct:

For both sources the compression factor $K(N)$ is smaller for $N = 50000$ than for $N = 10000$.
The same applies to the residual redundancy: $r(N = 50000) < r(N = 10000)$.
Both with regard to $K(N)$ and $r(N)$ "more favourable" values result with larger $N$ , even if, as with the redundancy-free binary source $\rm BQ2$ , the application of Lempel–Ziv actually leads to a deterioration.