Exercise 2.13Z: Combination of BWT and MTF
From LNTwww
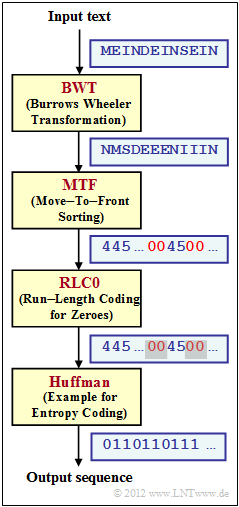
We refer to the theory page Application Scenario for the Burrows-Wheeler Transform and consider the coding system sketched on the right, consisting of the blocks.
- Burrows–Wheeler–Transformation $\rm (BWT)$ as described in Exercise 2.13; the two character sets at the input and output of the BWT are the same: $\{$ $\rm D$, $\rm E$, $\rm I$, $\rm M$, $\rm N$, $\rm S$ $\}$;
- Move–to–Front $\rm (MTF)$, a sorting algorithm that outputs a string of the same length $($ $N = 12 in the example)$, but with a different alphabet $\{$0, 1, 2, 3, 4, 5$\}$ ;
- $\rm RLC0$ – a run-length encoding specifically for zero, which is (as) frequent according to $\rm BWT$ and $\rm MTF$ ; all other indices are not changed by $\rm RLC0$ ;
- $\rm Huffman$ as described in the chapter Entropy coding according to Huffman; frequent characters are represented by short binary sequences and rare ones by long ones.
The $\rm MTF$–algorithm can be described as follows for $M = 6$ input symbols:
- The output sequence of the $\rm MTF$ is a string of indices from the set
- $ I = \{$0, 1, 2, 3, 4, 5$\}$.
- Before starting the actual $\rm MTF$ algorithm, the possible input symbols are sorted lexicographically and assigned to the following indices:
- $\rm D$ → 0, $\rm E$ → 1, $\rm I$ → 2, $\rm M$ → 3, $\rm N$ → 4, $\rm S$ → 5.
- Let the $\rm MTF$ input string here be $\rm N\hspace{0.05cm}M\hspace{0.05cm}S\hspace{0.05cm}D\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}N\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}N$. This was the $\rm BWT$ result in Exercise 2.13. The first $\rm N$ is represented as $I = 4$ according to the default setting.
- Then the $\rm N$ is placed at the beginning in the sorting, so that after the coding step $i = 1$ the assignment holds:
- $\rm N$ → 0, $\rm D$ → 1, $\rm E$ → 2, $\rm I$ → 3, $\rm M$ → 4, $\rm S$ → 5.
- Continue in the same way until the entire input text has been processed. If a character is already at position 0, no reordering is necessary.
Hints:
- The task belongs to the chapter Other source coding methods.
- In particular, reference is made to the page Burrows–Wheeler Transformation.
- Information on the Huffman code can be found in the chapter Entropy Coding according to Huffman. This information is not necessary for the solution of the task.
Questions
Musterlösung
(1) Die Grafik auf der Angabenseite zeigt, dass die Lösungsvorschläge 1 und 2 richtig sind und der Vorschlag 3 falsch ist:
- $\rm E$ und $\rm I$ treten zwar gruppiert auf,
- aber nicht die $\rm N$–Zeichen.
(2) Richtig sind die Lösungsvorschläge 2 und 3:
- Die Eingangsfolge wird Zeichen für Zeichen abgearbeitet. Auch die Ausgangsfolge hat somit die Länge $N = 12$.
- Tatsächlich wird die Eingangsmenge $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$ in die Ausgangsmenge $\{ \hspace{0.05cm}\rm 0,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 3,\hspace{0.05cm} 4 , \hspace{0.05cm} 5 \}$ gewandelt.
- Allerdings nicht durch einfaches Mapping, sondern durch einen Algorithmus, der nachfolgend skizziert wird.
(3) Richtig ist der Lösungsvorschlag 2:
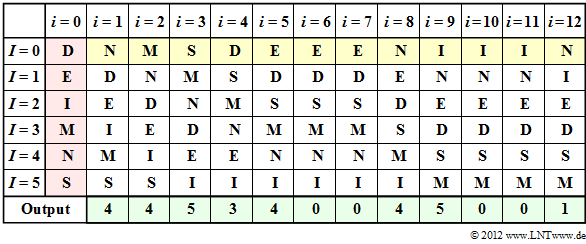
- Die Tabelle zeigt den MTF–Algorithmus. Der Schritt $i=0$ (rote Hinterlegung) gibt die Vorbelegung an. Die Eingabe der MTF ist gelb hinterlegt, die Ausgabe grün.
- Im Schritt $i=1$ wird das Eingangszeichen $\rm N$ entsprechend der Spalte $i=0$ durch den Index $I = 4$ dargestellt. Anschließend wird $\rm N$ nach vorne sortiert, während die Reihenfolge der anderen Zeichen gleich bleibt.
- Das Eingangszeichen $\rm M$ im zweiten Schritt erhält entsprechend der Spalte $i=2$ ebenfalls den Index $I = 4$. In gleicher Weise macht man weiter bis zum zwölften Zeichen $\rm N$, dem der Index $I = 1$ zugeordnet wird.
- Man erkennt aus obiger Tabelle weiter, dass zu den Zeitpunkten $i=6$, $i=7$, $i=10$ und $i=11$ der Ausgabeindex jeweils $I = 0$ ist.
(4) Richtig sind die Aussagen 1 und 2:
- Die Vorverarbeitungen "BWT" und "MTF" haben nur die Aufgabe, möglichst viele Nullen zu generieren.
(5) Alle Aussagen sind richtig.
- Nähere Angaben zum Huffman–Algorithmus finden Sie im Kapitel "Entropiecodierung nach Huffman".