Exercise 2.13: Inverse Burrows-Wheeler Transformation

To be analysed
BWT result

Die Burrows–Wheeler–Transformation – abbreviated $\rm BWT$ – causes a blockwise sorting of the characters of a text with the aim of preparing the text for efficient data compression with the help of run-length coding or entropy coding.

First, an $N×N$– matrix is generated from a block of length $N$ , with each row of this first–matrix resulting from the preceding row by cyclic left shift.

Then the matrix is sorted lexicographically (without special characters: alphabetically) . The result of the BWT is the last row of the new BWT matrix, the so-called $\text{L–column}$ (from "Last", last row of the BWT–matrix).

Further, this task refers to the $\text{F–column}$ (from "First", first row of the BWT matrix), which is needed for the inverse Burrows–Wheeler–Transformation ⇒ reconstruction of the original text from the L–column.

For the inverse BWT, the so-called primary index $I$ is also required. This indicates the row of the BWT matrix in which the algorithm must be started.

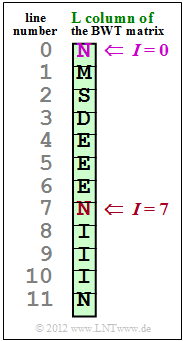
The graphic shows the result of a BWT, more precisely its L–column. The original text is to be reconstructed from this according to the description on the theory page Burrows–Wheeler Transformation ,

where in subtask (2) from the primary index $I = 7$
and in subtask (3) $I = 0$ is to be assumed.

Hints:

The exercise belongs to the chapter Other source coding methods.
In particular, reference is made to the page Burrows–Wheeler Transformation.
Further information can be found in the two publications mentioned below:

(1) Abel, J.: Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation.
In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140–144, Sept. 2003.

(2) Abel, J.: Grundlagen des Burrows-Wheeler-Kompressionsalgorithmus.
In: Informatik Forschung & Entwicklung, no. 2, vol. 18, S. 80–87, Jan. 2004.

Questions

Solutions

Solution

(1) Solution suggestion 3 is correct:

The first column of the BWT matrix is also called the F–column and the last column the L–column (from "First" or "Last").
Only the L–column is passed on to the next coding level.
The F–column, which is also needed for the reverse transformation, results from the L–column by lexicographic sorting.

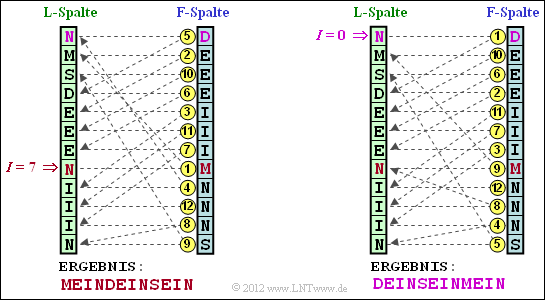
(2) Solution suggestion 1 is correct: MEINDEINSEIN is correct, as can be seen from the left-hand representation of the following diagram.
Note that the top line represents the line number $I = 0$ in each case. For explanation:

BW back transformation with $I = 7$ (left) or $I = 0$ (right)

Start the decoding with the line $I = 7$ of the F–column. The content is "M".
Search for the corresponding "M" in the L–column and find it in line number "1".
From line 1 of the L–column one goes horizontally to the F–column and finds the symbol "E".
Similarly, one finds the third output symbol "I" in line 4 of theF–column.
The decoding algorithm ends with the output symbol "N" in the third last row.

(3) Correct is the proposed solution 2:

$\rm DEINSEINMEIN$, as shown in the graph on the right.
(4) Correct is the suggested solution 3:

In BWT, four characters here are equal to their predecessors, in the original none.
In the F–column , even more characters would be the same as their respective predecessors (6 in total) due to the lexicographical sorting, but this sorting cannot be reversed without loss.
Solution suggestion 1 is also wrong: the original and BWT contain exactly the same characters $($three times $\rm E$, three times $\rm I$, three times $\rm N$ and one each of $\rm D$, $\rm M$ and $\rm S)$.

	The result is the original text, read from back to front.
	The result is a cyclic permutation of the original.
	It results in more favourable character frequencies.
	All characters are sorted lexicographically.
	Identical characters follow each other more often in the BWT.

	$\rm SEINMEINDEIN$,
	$\rm NIIINEEEDSMN$,
	$\rm DEEEIIIMNNNS$.